一类集值映射在迭代下集值点和集值区间的变化
章静静, 李 林
(嘉兴学院数理与信息工程学院,浙江嘉兴314001)
对于一个非空集合X和一个正整数n,映射f:X→X的n次迭代可定义为:fn(x)=f(fn-1(x)),∀x∈X.特别地,记f0(x)≡x.近几十年来由于关于周期性的Sharkovsky序、关于分岔的Feigenbaum现象、关于运动复杂性的Smale马蹄等重大发现的不断涌现,动力系统的新成就促进了迭代函数方程的发展.关于映射迭代的研究,至少可追溯到一百多年以前 E.Schröder[1]、N.H.Abel[2]、C.Babbage[3]等数学家的工作.由于迭代工作与代数运算的迥然不同,研究工作艰难曲折[4-12].对于一些具体函数的迭代研究目前主要是关于多项式函数、折线函数[13-16]等一些特殊的非单调函数.例如金蕾等[17]对高次多项式这类非线性映射通过共轭相似法给出了一般的n次迭代计算结果,并且讨论了f(x)=1/(a+bxr)1/r这类非多项式型映射的迭代,给出了二维映射F:(x,y)→(u(x,y),v(x,y))在u(x,y)和v(x,y)均为线性函数时的n次迭代结果.L.Li[18]在2007年研究了区间上单折点的折线函数的迭代,研究其折点的个数不会增加或者有界的条件.孙太祥等又讨论了区间I=[0,1]上所有的平顶单峰和双峰自映射的迭代问题[19-20].最近,文献[21]给出了一类单集值点映射在迭代下集值点个数不增的条件.
令2X为X的所有子集构成的族,则称映射F:X→2X为X上的一个集值映射,而X中取到集值的点称为集值点.进一步,对于X中的任意子集Y⊂X,其像F(Y)定义为,那么F的n次迭代Fn定义为,其中F0(x):={x},x∈X.
本文讨论的是一类定义在单位区间I=[0,1]上具有单个集值点的严格单调映射的迭代.这类集值映射可定义为

其中A⊂I为F的集值区间,而F1和F2分别是定义在[0,c)和(c,1]上的线性函数,并满足以下条件之一:
显然,F为定义在I=[0,1]上的上半连续函数.文献[12]研究了这类集值映射在迭代下集值点个数不增的条件,并给出该条件下映射迭代的表达式.将推广文献[9,12]中的结论,研究该函数在迭代下的集值区间的变化,并给出一般的迭代表达式.为方便起见,令V(F)表示函数F的集值点个数,l(F)为F的集值区间.
1 F1、F2为严格递增的连续函数
在F1和F2严格递增的情形下,注意到集值点个数V(Fn)取决于函数值与c的关系.为行文方便,称单位区间[0,1]上的一个递增(或递减)的数列为m次跨越c∈(0,1),如果存在正整数m≥2有xi


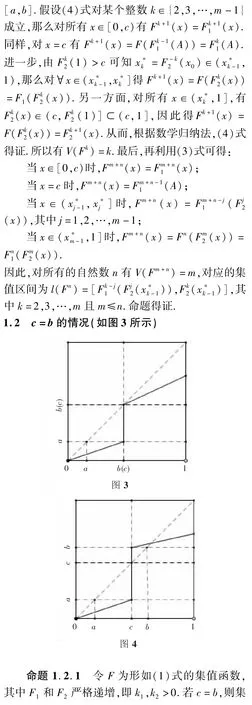



2 F1、F2为严格递减的连续函数





[1]Schröder E.ber Iterate funktionen[J].Math Ann,1871,3:295-322.
[2]Abel N H.Oeuvres completes[J].Christiana,1881,II:36-39.
[3]Dubbey J M.The Mathematical Work of Charles Babbage[M].New York:Cambridge University Press,1978.
[4]Chen J M,Zhang W N.Leading coefficient problem for polynomial-like iterative equations[J].J Math Anal Appl,2009,349:413-419.
[5]Li L,Yang D L,Zhang W N.A note on iterative roots of PM functions[J].J Math Anal Appl,2008,341:1482-1486.
[6]Li L,Zhang W M.Continuously decreasing solutions for polynomial-like iterative equations[J].Sci China,2013,A56:1051-1058.
[7]Li L,Zhang W N.Construction of usc solutions for a multivalued iterative equation of ordern[J].Results Math,2012,62:203-216.
[8]Liu L,Jarczyk W,Li L,et al.Iterative roots of piecewise monotonic functions of nonmonotonicity height not less than 2[J].Nonlinear Anal,2012,75:286-303.
[9]Liu L,Zhang W N.Non-monotonic iterative roots extended from characteristic intervals[J].J Math Anal Appl,2011,378:359-373.
[10]Shi Y G,Li L,Lesniak Z.On conjugacy ofr-modal interval maps with nonmonotonicity height equal to 1[J].J Difference Equ Appl,2013,19:573-584.
[11]Xu B,Zhang W.Construction of continuous solutions and stability for the polynomial-like iterative equation[J].J Math Anal Appl,2007,325:1160-1170.
[12]Zhang W M,Zhang W N.Continuity of iteration and approximation of iterative roots[J].J Comput Appl Math,2011,235:1232-1244.
[13]Yang L L,Yang L,Yu Z H,et al.Real polynomial iterative roots in the case of nonmonotonicity height≥2[J].Sci China,2012,A55:2433-2446.
[14]Yu Z H,Yang L,Zhang W N.Discussion on polynomials having polynomial iterative roots[J].J Symb Comput,2012,47(10):1154-1162.
[15]李林.折线函数与集值函数的迭代与迭代根[D].成都:四川大学,2007.
[16]Zhang W X,Zhang W N.Computing iterative roots of polygonal functions[J].J Comput Appl Math,2007,205:497-508.
[17]金蕾,周喆,刘旭.迭代的计算与估计[J].数学的实践与认识,2004,34(4):170-175.
[18]Li L.Number of vertices for polygonal functions under iteration[J].Korea Soc Math Educ,2007,14:99-109.
[19]孙太祥,蒋运然.区间上平顶单峰自映射的迭代根[J].广西科学,2000,7(2):111-114.
[20]孙太祥,席鸿建.区间上平顶双峰连续自映射的迭代根[J].系统科学与数学,2001,21(3):348-361.
[21]李林,林淑容,李春晔.一个集值映射在迭代下集值点个数不增的条件[J].四川大学学报:自然科学版,2010,47:17-20.
[22]Aubin J P,Frankowska H.Set-Valued Analysis[M].Boston,Basel,Berlin:Birkhauser,1990.
[23]Babbage C.Essay towards the calculus of functions[J].Philosoph Transact,1815:389-423.
[24]Baron K,Jarczyk W.Recent results on functional equations in a single variable,perspectives and open problems[J].Aequationes Math,2001,61:1-48.
[25]Kuczma M.Functional equation in a single variable[C]//Monografie Mat.Warszawa:Polish Scientific Publishers,1968,46.
[26]Kuczma M,Choczewski B,Ger R.Iterative functional equations[C]//Encyclopedia of Mathematics and Its Applications.Cambridge:Cambridge University Press,1990,32.

