输电线路杆塔构件可靠度校准

冯云芬，贡金鑫，李宏男，张子引

(1.大连理工大学建设工程学部，辽宁省大连市 116024；2.国网北京经济技术研究院，北京市 102209)

输电线路杆塔构件可靠度校准

冯云芬1，贡金鑫1，李宏男1，张子引2

(1.大连理工大学建设工程学部，辽宁省大连市 116024；2.国网北京经济技术研究院，北京市 102209)

为确定跨越高速铁路输电线路的可靠度水平，分析计算杆塔构件荷载、抗力的统计参数，对按现行规范设计的输电线路杆塔构件的可靠度进行了校准。分析表明，在永久荷载与风荷载组合下，构件轴心受力强度的可靠指标平均约为3.10，构件轴心受压稳定的可靠指标平均约为2.99；在永久荷载与风荷载和覆冰荷载的组合下，构件轴心受力强度的可靠指标平均约为3.35，构件轴心受压稳定的可靠指标平均约为3.20。永久荷载与风荷载组合时我国输电线路杆塔杆件的可靠度水平比建筑钢结构的可靠度略低；永久荷载与风荷载组合及永久荷载、风荷载与覆冰组合时，我国输电线路杆塔杆件的可靠度水平与美国杆塔构件的可靠度水平相近，比加拿大杆塔构件的高。

输电线路；杆塔构件；可靠度；校准

0 引 言

随着我国经济的高速发展，对电力的需求呈直线增长趋势，因此电力系统的发展成为一种必然趋势。输电线路体系是高负荷电能输送的载体，近年来逐渐趋于向大型化复杂化方向发展。因此，对输电塔线路体系的设计理论、结构安全性都提出了新的要求。与此同时，近年来随着我国高速铁路的迅速发展，输电线路跨越高铁的情况经常出现。为保证高铁的安全运行，对输电线路跨越提出了更高的要求。因为铁路基础设施与输电线路采用不同的设计方法，设计规范中材料强度的取值、分项系数或安全系数的含义不同，单从设计规范出发并不能明确铁路设施与输电线路的安全度。因此，需要采用同一个尺度进行分析和协调。

自20世纪80年代以来，可靠度理论在结构设计和规范中的应用得到了很大发展。结构可靠度理论是用概率方法描述结构的安全性，综合考虑了荷载、材料性能、几何尺寸、计算方法等不确定性，可靠指标能够作为一个统一的尺度衡量不同结构的安全性。从国际范围讲，结构可靠度理论目前在建筑、桥梁等领域的应用相对比较成熟，然而在输电线路体系的应用尚处于启动状态，一些学者已对此进行了探讨[1-8]。国外一些电力系统的设计规范正向基于可靠度理论的设计方法过渡，如美国标准NESC C2—2002《美国国家电力安全规范》[9]和ASCE 74—2009《输电线路结构荷载设计导则》[10]、加拿大规范CSA C22.3 No. 1—2001《高架线路系统》[11]、欧洲规范EN 50341《超AC 45KV架空输电线路》[12]和国际标准IEO 606826—2003《架空输电线路设计标准》等[13]。在铁路工程领域，我国在20世纪90年代颁布了GB 50216—94《铁路工程结构可靠度设计统一标准》，自2011年开始，铁路工程领域启动了铁路工程设计规范由容许应力或安全系数设计法向可靠度设计法转轨的工作。

为适应我国电力系统由传统的高压、超高压输电技术向特高压输电技术发展，满足跨越高速铁路输电线路的安全要求，对跨越高速铁路的输电线路的可靠度进行了研究。本文的目的是确定按现行DL/T 5154—2002《架空送电线路杆塔结构设计技术规定》设计的输电线路杆塔构件的可靠度水平。

1 荷载效应和抗力统计参数

输电线路体系由输电杆塔、绝缘子、金具和导、地线组成。杆塔构件应具有能够承受自身重力、风荷载、覆冰荷载、温度等作用的能力。对输电线路杆塔构件及各组成部分进行可靠度分析和设计，首先要确定线路荷载效应和抗力的概率分布和统计参数。

1.1 荷载效应的统计参数

荷载效应是荷载使结构或构件产生的内力、变形等，一般认为荷载效应与荷载的概率分布是一致的。因此研究荷载效应的概率分布，只需研究荷载的概率分布。荷载的统计参数一般用均值系数(平均值与标准值的比值)和变异系数(标准差与平均值的比值)来表示。

杆塔设计中为便于荷载组合，荷载往往是按方向进行分类的。由于不同荷载的概率特性不同，可靠度分析中是按荷载随时间变化的特性进行分类的，即将荷载分为永久荷载、可变荷载(风荷载和覆冰荷载)[14]。

1.1.1 永久荷载

在输电线路中，永久荷载G包括杆塔构件、绝缘子、导地线等的自重。根据以往的统计资料，自重一般服从正态分布。参考建筑结构的统计分析结果，取自重的均值系数kG=1.06，变异系数δG=0.07。

1.1.2 风荷载

风荷载W是输电线路承受的主要可变荷载之一。风荷载对输电线路的作用机理比较复杂，输电线路采用的风荷载计算方法与建筑结构相同，所以输电线路可靠度分析时风荷载采用与建筑结构相同的概率分布和统计参数。风荷载服从极值I型分布。设计中考虑下面风荷载的2种荷载组合。

(1) 自重与风组合。

当自重与风荷载组合时，采用30 m/s风速作为代表风速，将该风速作为对应于设计基准期的标准值Wk的标准风速。采用建筑结构的统计参数，风荷载均值系数和变异系数为：kWT=0.908、δWT=0.193。

(2) 自重、风荷载和覆冰荷载组合。

当自重与风荷载和覆冰荷载组合时，采用10 m/s的风速作为代表风速，风荷载降低。假定10 m/s的风速为1年中覆冰最大的1个月的最大风速，则风荷载平均值按式(1)估算：

(1)

式中：μWt为永久荷载与风荷载和覆冰组合中风荷载的平均值；μWT和σWT为永久荷载与风荷载组合中风荷载的平均值和标准差；αWT为极值Ⅰ型分布的尺度参数；t取1个月；T为风荷载重现期，取50年。

永久荷载与风荷载和覆冰荷载组合时，风荷载的均值系数为0.034。假定此时的风荷载变异系数仍为0.193。

1.1.3 覆冰荷载

天空中的“过冷却”水滴、湿雪碰到温度较低的导地线或绝缘子等部件时，便会在其表面冻结成冰，称之为覆冰。导线覆冰的机理非常复杂，影响导线覆冰的因素也很多，主要有气象条件、地形及地理条件、海拔高度、凝结高度、导线悬挂高度、导线直径、导线扭转性能、风速风向、水滴直径、电场强度及负荷电流等。

1.2 抗力统计参数

抗力为结构或元件抵抗荷载作用的能力，其不确定性来自于3个方面，即材料性能不确定性、几何尺寸不确定性和计算模式不确定性。同荷载效应一样，抗力的统计参数也用均值系数和变异系数表示。

1.2.1 构件轴心受力

根据DL/T 5154—2002《架空送电线路杆塔结构设计技术规定》，并考虑公式的计算误差，杆塔构件轴心受力时的抗力可表示为

R=ΩP 1mAf

(2)

式中：ΩP 1为轴心受力强度时抗力计算模式不定性系数(随机变量)；m为构件强度折减系数(常数)；A为构件截面面积(随机变量)；f为构件材料强度(随机变量)。

抗力的均值系数和变异系数为：

(3)

(4)

式中：μR、μA和μf分别为抗力、构件截面面积和钢材强度的平均值；kP1、kA、kf和δP1、δA、δf分别为计算模式不定性、截面面积和钢材强度的均值系数和变异系数；Rk、Ak和fk分别为抗力、截面面积和钢材强度的标准值，其中fk按规范DL/T 5154—2002取值。各变量的统计参数见表1[16]。

由式(3)和式(4)确定的杆塔构件轴心受力时抗力的统计参数为kR=1.134，δR=0.117，抗力服从对数正态分布。

表1 构件轴心受力时抗力的统计参数

1.2.2 构件受压稳定

同样，根据DL/T 5154—2002《架空送电线路杆塔结构设计技术规定》，考虑公式的计算误差，杆塔构件轴心受压构件的稳定承载力表示为

R=ΩP2φmNAf

(5)

式中：ΩP2为抗力计算模式不定性系数(随机变量)；φ为轴心受压构件稳定系数(随机变量)；mN为系数(常数)；A为构件截面面积(随机变量)；f为构件材料强度(随机变量)。

抗力的平均值和变异系数为：

(6)

(7)

式中：μφ、δφ和kφ分别为构件受压稳定性系数的平均值、变异系数和均值系数；kP2和δP2分别为轴心受压稳定时抗力计算模式不定性的均值系数和变异系数；φk为稳定性系数的标准值。其中，kφ和δφ是按下述方法确定的，其他变量的统计参数见表1和表2。

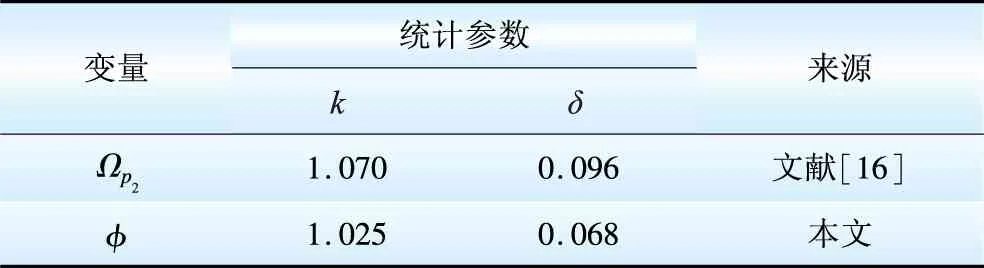
表2 构件轴心受压稳定抗力的统计参数

根据规范DL/T5154—2002[17]附录D，轴心受压构件稳定系数φ按式(8)计算：

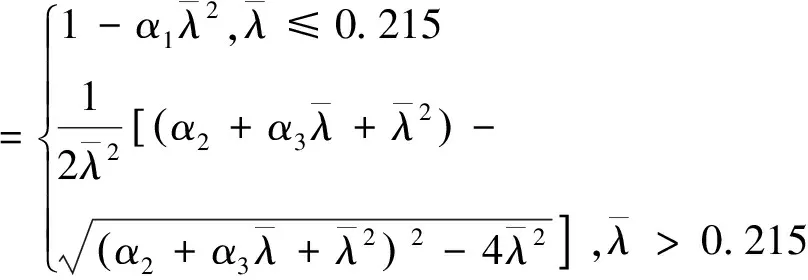
(8)

其中：

(9)

式中：λ为构件长细比；fy为钢材屈服强度；E为钢材弹性模量；α1、α2和α3为系数，根据DL/T 5154—2002附录D中表D3的截面分类按表D4取值[17]。

由于在式(8)中，稳定系数φ是用分段函数表示的，直接采用数学方法确定φ的概率分布函数及平均值和变异系数比较复杂。为了确定参数稳定系数φ的均值系数kφ和变异系数δφ，将钢材屈服强度fy和弹性模量E作为随机变量，根据fy和E的概率分布通过Monte Carlo模拟产生10 000组fy和E的随机数，将其代入式(8)得到φ的样本值。通过统计分析分别确定了构件长细比λ为10、50和100时轴心受压构件稳定系数的统计参数，如表3所示。图1给出了λ=50时b类截面在不同钢号下比值φ/φk的直方图。根据表3的分析结果，φ的均值系数取为kφ=1.025，变异系数δφ取为0.068。

表3 φ/φk的平均值及变异系数

图1 b类截面长细比λ=50时φ/φk的频率直方图

由式(6)和式(7)求得的杆塔构件轴心受力时稳定抗力的统计参数kR=1.185，δR=0.150。

1.3 荷载、抗力统计参数汇总

输电线路荷载及塔杆构件抗力的统计参数和概率分布汇总于表4。

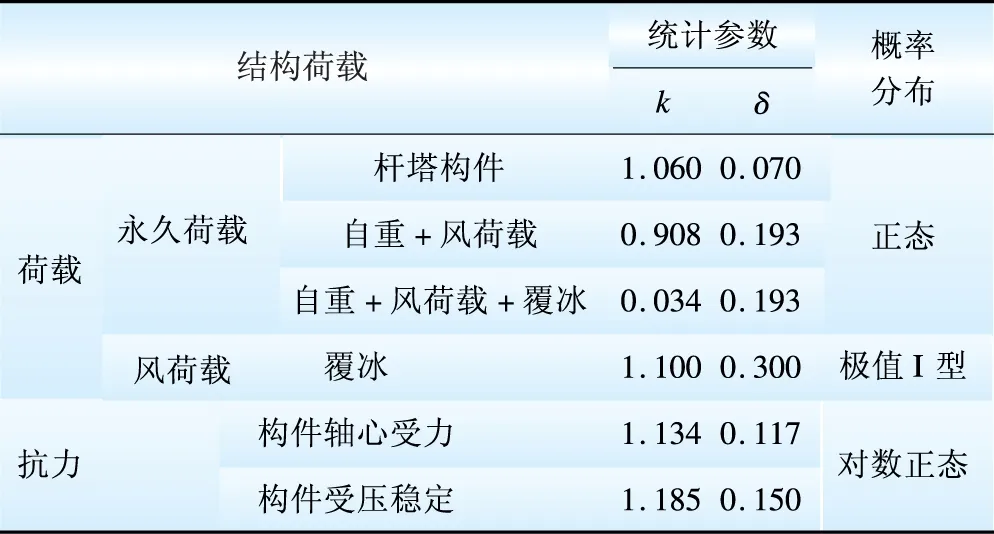
表4 荷载、杆塔构件抗力的统计参数

2 可靠度校准

2.1 基本设计表达式

结构可靠度校准是计算结构或结构构件按规范设计表达式设计，刚好满足规范要求时的可靠度，反映了设计规范的最低安全水平。我国标准GB 50545—2010《110 kV～750 kV架空输电线路设计规范》[18]中采用的分项系数设计表达式为

(10)

式中：γ0为杆塔结构重要性系数，重要线路不小于1.1，临时线路取0.9，其他线路取1.0；γG为永久荷载分项系数，对结构受力有利时不大于1.0，不利时取1.2；γQi为第i个可变荷载的分项系数，取1.4；SGk、SQik分别为永久荷载效应标准值、第i个可变荷载效应标准值；Rd为结构构件的抗力设计值，根据规范GB 50545—2010第8章，不同构件采用不同的抗力表达式；φ为可变荷载组合系数，正常运行情况取1.0，断线情况、安装情况和不均匀覆冰情况取0.9，验算情况取0.75。

根据式(10)，满足规范最低要求的抗力设计值为：

Rd=γ0(γGSGk+φ∑γQiSQik)

(11)

2.2 构件可靠指标计算

2.2.1 抗力计算

(1)构件轴心受力。

我国DL/T 5154—2002《架空送电线路杆塔结构设计技术规定》，构件轴心受力时的强度计算应满足：

(12)

式中：An为构件净截面面积；fd为钢材的强度设计值；m为构件强度折减系数。

满足规范最低要求的轴向力为

N=Rd=mAnfd

(13)

由式(11)和式(13)可得出：

(14)

式中：NGk和NQik分别为永久荷载和第i个可变荷载产生的轴向力标准值。

(2)构件受压稳定。

同样，根据标准DL/T 5154—2002的规定，构件轴心受压稳定的计算应满足：

(15)

式中：φk为铁塔构件轴心受压时的稳定系数，按DL/T 5154—2002确定。

由式(14)和式(15)得：

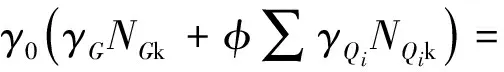
(16)

2.2.2 可靠指标计算

考虑永久荷载与风荷载组合及永久荷载与风荷载和覆冰荷载组合2种情况。构件轴心受压稳定时的分析除抗力统计参数与轴心受力构件不同外，功能函数、荷载和抗力的平均值和标准差与构件轴心受力的表达方式均相同，下面以构件轴心受力的情况为例说明可靠指标的计算过程。

(1)永久荷载与风荷载组合。

可靠度计算时将设计中的变量视为随机变量，构件轴心受力时的功能函数为

Z=R-NG-NW

(17)

式中：R为构件抗力；NG为永久荷载产生的轴力；NW为风荷载产生的轴力。

永久荷载和风荷载的平均值和标准差分别为：

(18)

(19)

抗力的平均值为

(20)

式中：kR为抗力的均值系数，如表4所示。

不同品种和厚度钢材强度的标准值和设计值如表5所示。

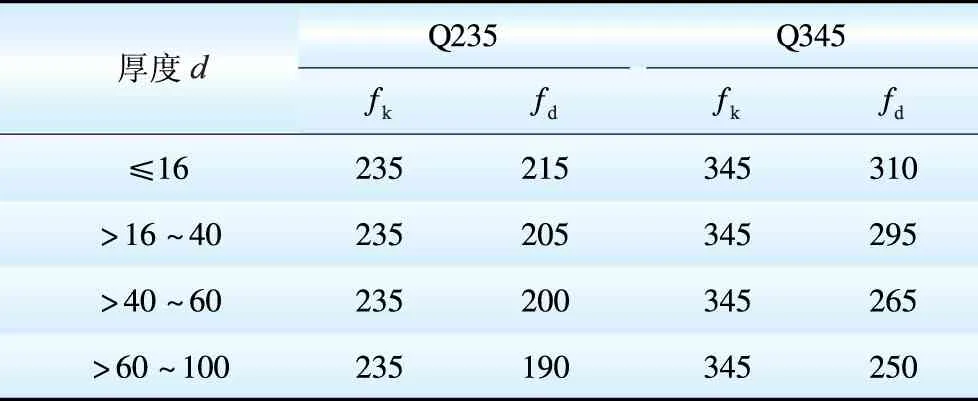
表5 钢材强度的标准值和设计值

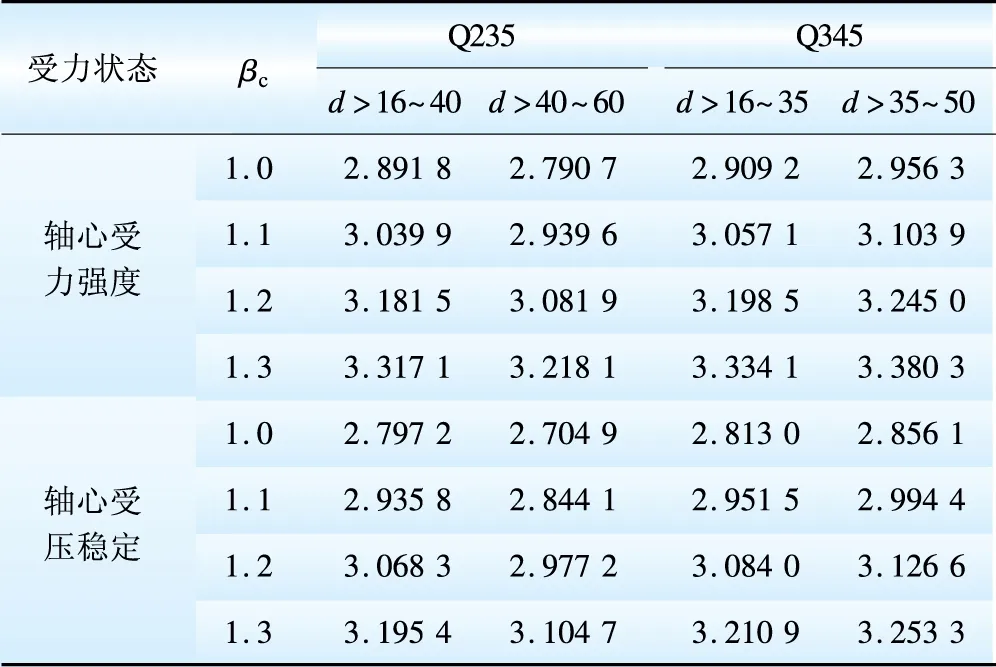
作用在杆塔上的风荷载包括风吹动杆塔构件产生的风荷载和风吹动绝缘子、金具和导地线产生的风荷载。规范GB 50545—2010《110 kV～750 kV架空输电线路设计规范》规定，在计算作用于500 kV和750 kV的杆塔上导地线的风荷载时(不包括导地线张力弧垂计算和风偏角计算)，还需考虑表6中的风荷载调整系数βc。根据设计经验，风吹动绝缘子、金具和导地线产生的风荷载一般为总风荷载的一半，将式(14)代入式(20)得：

(21)

式中γQ1为风荷载的分项系数。

表6 风荷载调整系数βc

由式(18)、式(19)和式(21)可以看出，结构抗力、永久荷载效应和风荷载效应的平均值和标准差均与永久荷载标准值NGk成正比，因此，计算可靠指标时，无需涉及荷载效应和抗力的具体值，仅与风荷载效应比ρW的取值有关。

根据多个实际输电塔的分析，取ρW=0.1～100。当永久荷载与风荷载组合时，采用JC方法计算得到的不同风荷载调整系数时不同钢号杆塔构件可靠指标随ρW的变化趋势，如图2和图3所示，不同钢号和风载调整系数时的平均可靠指标见表7。

由图2和图3可以看出，杆塔构件可靠指标与荷载比值ρW有关。荷载比值ρW≤1.0时，构件轴心受力强度的可靠指标随ρW的增加而增大；而ρW>1.0时，构件轴心受力强度的可靠指标随ρW的增大而减小。由表7可知，构件平均可靠指标随着风荷载调整系数βc的增大而增大，构件轴心受压稳定的可靠指标小于轴心受力强度的可靠指标。

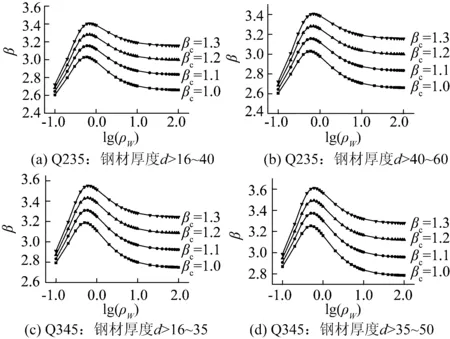
图2 构件轴心受力强度的可靠指标(永久荷载+风荷载)

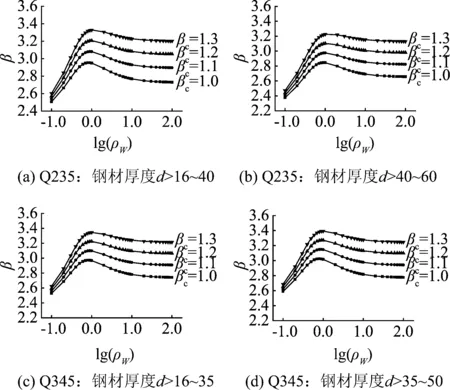
图3 轴心受压稳定的可靠指标(永久荷载+风荷载)

表7不同钢号构件的平均可靠指标(永久荷载+风荷载)

Tab.7Reliabilityindexesofmembersofdifferentsteelgrades(deadload+windload)

(2)永久荷载、风荷载和覆冰荷载组合。

仍以构件轴心受力强度的情况说明。永久荷载、风荷载和覆冰荷载组合时，构件轴心受力强度的功能函数为：

Z=R-NG-NW-NI

(22)

那么，覆冰组合下风荷载效应和覆冰荷载效应的平均值和标准差为：

(23)

(24)

式中：kNWI，δNWI，kNI，δNI分别为覆冰组合下风荷载和覆冰荷载的均值系数和变异系数。

构件轴心受压强度抗力的平均值为

(25)

式中γQ2分别为覆冰荷载的分项系数。

对于永久荷载+风荷载+覆冰荷载组合，覆冰荷载起控制作用。根据对实际输电杆塔的计算分析，覆冰荷载与永久荷载标准值产生的轴力之比ρI可取0.02～5，覆冰工况下风荷载与永久荷载标准值产生的轴力之比ρWI可取0.02～10。采用JC法计算的杆塔构件不同钢号轴心受力强度和轴心受压稳定的可靠指标随ρI和ρWI的变化趋势如图4和图5所示，每种情况下的平均可靠指标如表8所示。

由图4和图5可看出，在永久荷载+风荷载+覆冰荷载的组合下，ρI一定时，不同ρWI对应的可靠指标随ρWI的增大而增大；ρWI一定时，可靠指标随着ρI的增大而降低。从表8可以看出，构件轴心受压稳定的可靠指标也小于轴心受力强度的可靠指标。

图4 构件轴心受力强度的可靠指标

图5 构件轴心受压稳定的可靠指标

文献[19]对国家标准GB 50010—2001《钢结构设计规范》的可靠度进行了校准，永久荷载与风荷载组合时的可靠指标为2.94，小于永久荷载与楼面活荷载组合时的可靠指标。在2006年瑞典斯德哥尔摩召开的第9届概率方法在电力系统应用国际会议上，文献[8]发表了对NESC C2—2002《美国国家电力安全规范》的可靠度校准结果，永久荷载与风荷载组合的可靠指标为2.36～3.01，永久荷载与风荷载和覆冰组合时杆塔构件的可靠指标为2.29～3.91；对加拿大标准CSA C22.3 No.1—2001《高架线路系统》的可靠度校准结果为，杆塔构件永久荷载与风荷载组合时的可靠指标为0.85～2.00，永久荷载与风荷载和覆冰组合时的可靠指标为1.68～2.78。

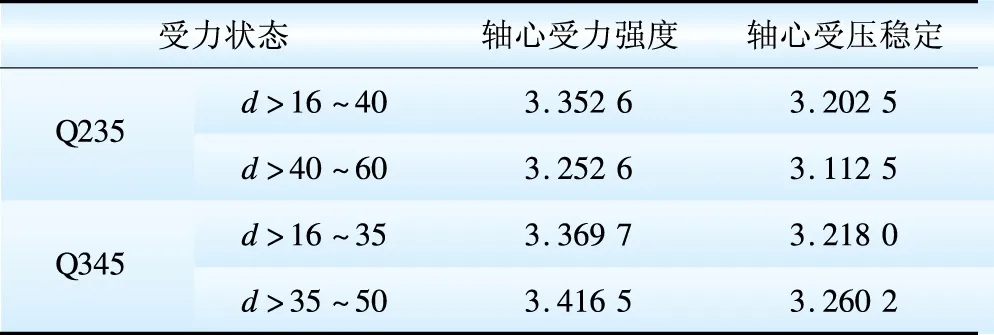
表8 不同钢号杆塔构件的可靠指标(永久荷载+风荷载+覆冰荷载)

由此可见，永久荷载与风荷载组合时我国输电线路杆塔杆件的可靠度水平比建筑钢结构的可靠度略低，与美国杆塔构件的可靠度水平相近，比加拿大杆塔构件的高；永久荷载、风荷载与覆冰组合时我国输电线路杆塔杆件的可靠度水平与美国杆塔构件的可靠度水平相近，比加拿大杆塔构件的高。

3 结 论

本文对按现行国家标准GB 50545—2010和行业标准DL/T 5154—2002规定设计的角钢杆塔进行了可靠度校准，明确了我国角钢杆塔构件的可靠度水平。分析得出如下结论：

(1)在永久荷载与风荷载组合下，构件轴心受力强度的可靠指标平均约为3.102 8，构件轴心受压稳定的可靠指标平均约为2.994 9；在永久荷载与风荷载和覆冰荷载的组合下，构件轴心受力强度的可靠指标平均约为3.347 9，构件轴心受压稳定的可靠指标平均约为3.198 3；

(2)永久荷载与风荷载组合时我国输电线路杆塔杆件的可靠度水平比建筑钢结构的可靠度略低。永久荷载与风荷载组合及永久荷载、风荷载与覆冰组合时，我国输电线路杆塔杆件的可靠度水平与美国杆塔构件的可靠度水平相近，比加拿大杆塔构件的高。

[1]梁德飞. 输电线路大跨越钢管塔的结构可靠度分析[J]. 武汉大学学报：工学版，2009，42(增刊)：249-252.

[2]李峰，袁骏，侯建国，等. 我国输电线路铁塔结构设计可靠度研究[J]. 电力建设，2010，31(11)：18-23.

[3]李茂华，李正，杨靖波，等. 特高压输电线路杆塔可靠度研究[J]. 电网技术，2010，34(5)：21-24.

[4]冯径军，柳春光，冯娇. 输电塔线在覆冰与风载下的可靠性分析[J]. 水电能源科学，2011，29(10)：203-206.

[5]秦力，张学礼，张杰，等. 浅析500 kV输电铁塔结构体系的可靠性[J]. 东北电力大学学报，2008，28(2)：9-12.

[6]侯建国，徐彬，董黛，等. 国内外架空输电线路设计规范安全度设置水平的比较[J]. 武汉大学学报：工学版，2011，44(增刊)：262-171.

[7]Haarlaa L, Pulkkinenb U, Koskinenc M, et al. A method for analysing the reliability of a transmission grid [J]. Reliability Engineering and System Safety, 2008, 93(2): 277-287.

[8]Guori B, Hong L. Achieved reliability of the North American design approaches for transmission overhead structures[C]//9th International Conference on Probabilistic Methods Applied to Power Systems, KTH, Stockholm, Sweden, 2006: 11-15.

[9]NESC C2—2002. National electrical safety code[S]. Institute of Electrical & Electronics Engineers, 2002.

[10]ASCE 74—2009. Guidelines for electrical transmission line structural loading[S]. American Society of Civil Engineers, 2009.

[11]CAN-CSA22.3 No.1. Canadian electrical code：overhead systems[S]. Canadian Standards Association, 2001.

[12]EN 50341-1. Overhead electrical lines exceeding AC 45 kV[S]. European Committee for Electrotechnical Standardization, 2001.

[13]IEC 60826—2003. Design criteria of overhead transmission lines[S]. International Electrotechnical Commission, 2003.

[14]贡金鑫，魏巍巍. 工程结构可靠性设计原理[M]. 北京：机械工业出版社，2007.

[15]蒋兴良，易辉. 输电线路覆冰及防护[M]. 北京：中国电力出版社，2002.

[16]黄兴棣. 工程机构可靠性设计[M]. 北京：人民交通出版社，1992.

[17]DL/T 5154—2002 架空送电线路杆塔结构设计技术规定[S]. 北京：中国电力出版社，2002.

[18]中国电力企业联合会. GB 50545-2010 110 kV～750 kV架空输电线路设计规范[S]. 北京：中国计划出版协会，2010.

[19]戴国欣，刘海鑫. 新钢结构设计规范总体安全度分析[J]. 建筑科学，2002,18(增刊)：73-75.

(编辑：张媛媛)

ReliabilityCalibrationofTowerMembersinTransmissionLine

FENG Yunfen1, GONG Jinxin1, LI Hongnan1, ZHANG Ziyin2

(1. Faculty of Infrastructure Engineering Dalian University of Technology, Dalian 116024, Liaoning Province, China;2.State Power Economic Research Institute, Beijing 102209, China)

To set the reliability level of transmission line crossing high speed railway, the statistical parameters of the load and resistance of tower members in transmission line were analyzed and calculated. The reliability of tower members designed based on the current code were calibrated. It is indicated that the reliability indexes for strength of axially loaded members or the stability of axial compression members are 3.10 and 2.99, respectively, in the combination of permanent load and wind load; and are 3.35 and 3.20 respectively, in the combination of permanent load, wind load and ice load. The reliability of tower member in transmission lines in China is somewhat lower than that of building steel structures, in the combination of permanent load and wind load; but it is close to the reliability of tower members in US, and higher than that in Canada, in the combination of permanent load and wind load, or in the combination of permanent load, wind load and ice load.

transmission line; tower member; reliability; calibration

国家自然科学基金委创新研究群体基金项目(51121005)；国家电网公司科技项目(B3440912K006)；高等学校学科创新引智计划资助项目(B08014)。

编者按

基于上述情况，本刊特邀国网北京经济技术研究院、大连理工大学等单位总结了“国家电网公司科技项目：输电线路跨越高铁关键技术研究”的相关成果，推出了“跨越高铁输电线路可靠度研究”专栏。本期共刊登相关论文5篇，内容涉及输电线路杆塔结构的可靠度校准、输电线路绝缘子、金具和导地线的可靠度校准、跨越高速铁路输电线路的目标可靠指标等。希望此次专栏为从事输电线路可靠度的科研工作人员提供一些参考和借鉴。本专栏得到了大连理工大学贡金鑫教授、李宏男教授以及国网北京经济技术研究院张子引高工、田雷高工的大力支持，在此一并表示感谢！

TM 732

： A

： 1000-7229(2014)05-0013-08

10.3969/j.issn.1000-7229.2014.05.003

2013-11-07

：2014-02-18

冯云芬(1982)，女，博士，主要从事工程结构可靠度与结构耐久性方面的研究工作，E-mail：fengyunfen@126.com；

贡金鑫(1964)，男，博士，教授，博士生导师，主要从事工程结构可靠度、数值分析及钢筋混凝土结构耐久性方面的研究工作，E-mail：gong_jx.vip@eyou.com；

李宏男(1958)，男，博士，长江学者特聘教授，博士生导师，主要从事大跨越输电塔体系的抗震计算理论、结构减震控制、重大工程健康监测与损伤评估等方面的研究工作，E-mail：hnli@dlut.edu.cn；

张子引(1971)，男，本科，高级工程师，主要从事输电线路设计技术研究及电网工程评审和咨询工作，E-mail：zhangziyin@chinasperi.sgcc.com.cn。

随着我国经济的迅猛发展，对电力需求直线增长，输电线路体系日趋大型化、复杂化；与此同时，我国高铁的迅速发展使得输电线路跨越高铁的情况经常出现。为保证高铁安全运行，对跨越高铁输电线路的可靠性提出了更高要求。由于输电线路与铁路基础设施的设计方法不同，设计规范中材料强度的取值、分项系数或安全系数的含义不同，因此，需要建立一个统一的尺度分析跨越高铁输电线路的安全性。