液膜蒸干模型在液态金属CHF预测中的应用
马在勇,仇子铖,巫英伟,田文喜,苏光辉,秋穗正
(西安交通大学 动力工程多相流国家重点实验室 核科学与技术系,陕西 西安 710049)
在反应堆堆芯、加热器等装置的设计中,临界热流密度(CHF)的准确预测具有十分重要的安全和经济意义。CHF总体上包括偏离核态沸腾(DNB)型和烧干型两种,针对这两种类型,已有大量的经验关系式和模型。针对DNB型的有边界层分离模型、气泡壅塞模型、界面抬升模型等,针对烧干型的有液膜蒸干模型、过热层蒸汽补给模型、三流体模型等。然而,这些模型主要是针对水、氟利昂等普通流体开发,模型中包含的大量经验关系式和相关常数的普适性还有待验证。
在已有的反应堆堆型中,水并非唯一的冷却剂,如快堆、钠冷行波堆中的冷却剂采用液态金属。在这些液态金属冷却的反应堆中,CHF的精确预测至关重要。依据实验数据和相似准则原理,研究者已提出一些经验关系式[1-3]。然而,经验关系式在应用时有很大的局限性,更为合理的CHF的预测是采用理论模型进行数值计算。本工作对采用液膜蒸干模型预测液态金属CHF进行尝试,并将数值计算结果与实验数据和经验关系式的计算结果进行比较。
1 模型相关关系式
液膜蒸干模型适于计算弥散环状流下的烧干型CHF。在弥散环状流流型下,液膜的厚度受3方面因素的影响,即液滴在液膜上的沉积、气芯对液膜的夹带和液膜因受热引起的蒸发,文献[4-5]通常假定液膜质量流量为零时即发生了CHF。考虑这些因素的液膜蒸干模型在水等常规流体中已得到成功应用[4-5]。液膜蒸干模型的基本表达式为液膜质量流量的连续方程:
πD(md-me-q/λ)
(1)
式中:Wlf为某一位置处液膜质量流量;D为圆管直径;md、me分别为单位面积的沉积率和夹带率;q为该位置的热流密度;λ为汽化潜热;z为圆管轴向位置坐标。
为获得不同位置处的液膜质量流量,需确定不同位置处的夹带率、沉积率等闭合关系式及环状流起始点和起始夹带份额等边界条件。文献[6]中总结了这几方面的大量经验关系式,这些经验关系式基本上均采用无量纲形式表示。本工作对相关关系式的选取如下。
沉积率使用Kataoka等[7]的关系式计算:
.
(2)
式中:μv、μl分别为流体蒸汽和液态下的黏性系数;Rel为液膜雷诺数;E为该位置处的液体夹带份额。
液膜雷诺数和液体夹带份额按下式计算:
Rel=ρlJlfD/μl
(3)
E=(Jl-Jlf)/Jl
(4)
式中:ρl为液体密度;Jl、Jlf分别为液体和液膜的表观速度。
根据Ishii等[8]的实验结果,夹带作用有4种机制,分别为波的滚动、波的切入、气泡破裂和液体冲击(图1)。在水的夹带研究中,考虑的机制仅包括波的滚动和气泡破裂。对于液态金属,由于流体具有良好的导热作用,同时液膜较薄,液膜内的过热度不足以产生气泡,因此气泡破裂的机制不需考虑[9]。

图1 液体夹带的4种机制
夹带作用并非在所有条件下均发生,而是必须满足一定的条件。对夹带的判定采用Ishii等[8]的准则:
Relfc=(y+/0.347)1.5(ρl/ρv)0.75(μv/μl)1.5
(5)
≥
(6)
≥1.
(7)
式中:ρv为蒸汽密度;Jvc为蒸汽临界表观速度;σ为表面张力系数;下标c表示发生夹带的临界值;Nμ为黏度数,按下式计算:

(8)
在满足夹带准则的条件下,夹带率按照Okawa等[10]的关系式计算:
(9)
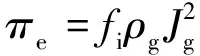
ke=6.8×10-4,n=0.5πe>0.295
ke=1.6×10-3,n=1.2
0.067 5<πe<0.295
ke=3.1×10-2,n=2.3πe<0.067 5
式中:δ为液膜厚度;n为经验常数。
对于液膜厚度δ的计算,很多文献采用冯·卡门速度分布和湍流摩擦系数相结合的方法,这种方法较为复杂且有些情况下不能给出合理结果。本工作采用Okawa等[11]依据气液界面处力的平衡给出的关系式计算:
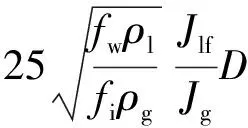
(10)
式中,fw、fi分别为壁面和液面的摩擦系数。
摩擦系数分别采用Wallis[12]关系式和Blasius关系式:
fi=0.005(1+300δ/D)
(11)

(12)
除以上关系式,还需确定环状流起始点和液滴起始夹带份额。环状流起始点通过含汽率xo确定[12]:
(13)
对于起始夹带份额,很多文献中按照平衡夹带份额给出。对于液态金属,按照Ishii等[13]的关系式将给出非常低的起始夹带份额,不能获得与实验数据符合良好的结果。Govan[14]的分析表明,CHF的预测结果对环状流起始夹带份额非常敏感,因此,本工作采用的起始夹带份额将依据对实验数据的最佳预测给出。
2 结果与讨论
为验证本模型对液态金属CHF的预测效果,将模型预测结果与实验数据和经验关系式进行比较。
液态金属CHF的实验数据并不丰富,可获得的实验数据更为稀少。本文采用Kottowski[15]和Aladyev等[16]的142组实验数据。实验工质为钠(仅5组数据)或钾,饱和温度范围为850~1 400 K,进口含汽率为-0.001~-0.45,长径比L/D为30~166,质量流速为40~400 kg/(m2·s)。图2示出本模型的预测结果与实验数据的比较。从图2可看出,模型对实验数据预测的相对误差基本在±30%以内,这表明所用模型在预测液态金属环状流烧干型沸腾临界时是有效的。计算表明,利用实验数据的参数,发生沸腾临界时出口平衡含汽率在0.65~0.85之间,而实验获得的出口含汽率在0.5~1之间,这一方面表明CHF计算中考虑液滴夹带沉积作用的重要性,另一方面也反映出本文模型在预测液态金属CHF方面尚不完备。本文模型中采用的关系式来源于常规流体,这可能对模型预测能力有所限制,为提高模型预测能力,有必要研究出适用于液态金属的相关关系式。

图2 液膜蒸干模型CHF预测值与实验数据的比较
应用最为广泛的Kottowski等[1]的关系式为:
q=0.216G0.807/(L/D)0.807(1-2xi)λ
(14)
式中:q为热流密度;xi为进口平衡含汽率。
采用Baroczy两相摩擦压降关系式和Ledinegg不稳定性准则,Chang等[2]提出如下理论关系式:
q=2.13Ghfg/(L/D)[1+0.352xi-(0.82+
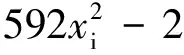
(15)
Katto[3]采用量纲分析和实验数据得到通用关系式:
q=0.25Ghfg/(L/D)(σρf/G2L)0.043(1-1.16xi)
(16)
图3示出上述实验数据与经验关系式的比较。从图3可看出,Kottowski等的关系式整体上高估了实验数据,但对预测结果的离散程度小;Chang等的关系式对实验数据的估计效果最好,特别是在CHF较小的区域,但在CHF较大时,有高估实验数据的趋势;Katto关系式为通用关系式,对实验数据的预测效果较差,在CHF较大时实验数据发散严重。总体而言,Chang等的关系式基于流动不稳定性得到,CHF较低时对应工况为流动不稳定的可能性高,因此在CHF较低时应采用此关系式;Kottowski等的关系式是基于大量实验数据拟合而得的,预测结果在CHF较高时有较高的准确度,因此在CHF较高时应采用此关系式;Katto关系式误差较大,不建议采用。
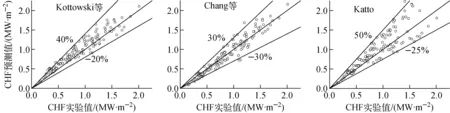
图3 不同关系式CHF预测值与实验数据的比较
由于相关实验数据特别是钠的较少,本文模型的可用性需进一步检验。为此,在一定参数范围内随机产生相关变量,将模型预测结果与经验关系式的进行比较。共生成937组钾的数据点和1 000组钠的数据点,相关变量的参数范围列于表1。在表1所列参数范围内,本文模型对钠、钾出口平衡含汽率的预测结果分别为0.65~0.95和0.55~0.9。
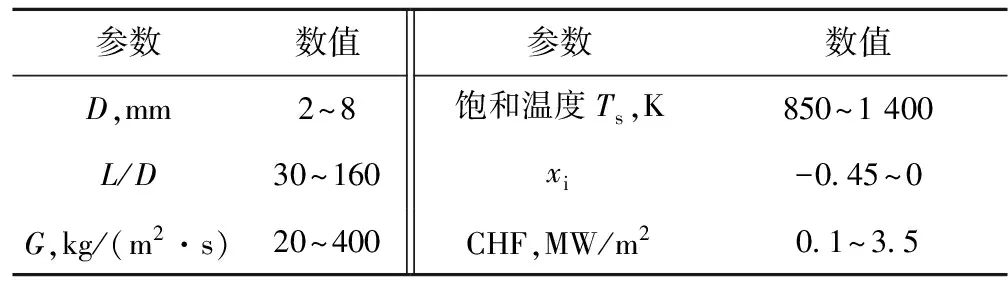
表1 生成的相关变量的参数范围
图4示出本文模型与Kottowski等的关系式预测的CHF的比较。值得注意的是,在CHF较低时,Kottowski等的关系式有时给出高于1的出口平衡含汽率,此时CHF依据出口平衡含汽率为1给出,这也表明Kottowski等的关系式在CHF较低时可能对CHF估计过高。从图4可看出,在CHF较低时,本文模型预测值较Kottowski等的关系式的偏低,且在此范围内钠、钾两种工质区别不大;在CHF较高时,本文模型对钾的预测有发散趋势,但对于钠的预测结果仍较好,但两种工质的预测结果仍在允许范围内。如前所述,Kottowski等的关系式在CHF较高时预测精度较高,由此可推测本文模型在CHF较大时对钠的预测效果较对钾的好,CHF过高时对钾CHF估计的精度可能不高。图5示出本文模型与Chang等的关系式预测的CHF的比较。由图5可看出,本文模型相对该关系式预测值偏高,但CHF较高时与该关系式符合较好。整体上看钠、钾预测结果区别不大,仅在CHF较高时模型对钠的CHF预测值略高。考虑到Chang等的关系式在CHF较低时有较高的准确性,可推测,本文模型在CHF较低时可能高估CHF。

图4 模型与Kottowski等的关系式预测的CHF比较
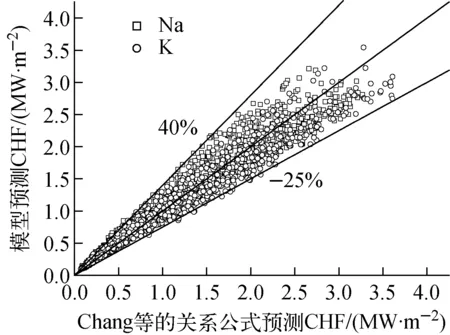
图5 模型与Chang等的关系式预测的CHF比较
3 结论
1) 对于液态金属环状流,必须考虑液滴沉积和夹带作用,由于液滴的沉积夹带作用,液态金属发生沸腾临界时的出口平衡含汽率可在0.55~0.95范围内变化。
2) 常规流体的沉积率、夹带率等相关关系式大体上可应用于液态金属,但在CHF较大时可能引起较大偏差,开发专门针对液态金属的相关关系式是必要的。
3) 依据实验数据,对于液态金属,初始夹带份额的推荐值为0.35。
4) 钠、钾两种液态金属在CHF较低时预测准确度区别不大,但在CHF较高时区别较为明显。
参考文献:
[1] KOTTOWSKI H, SAVATTERI C. Convective heat transfer and critical heat flux at liquid metal boiling[C]∥10th Meeting of the Liquid Metal Boiling Working Group. Karlsruhe: [s. n.], 1982.
[2] CHANG S H, LEE Y B. A new critical heat flux model for liquid metals under low heat flux-low flow conditions[J]. Nuclear Engineering and Design, 1994, 148(2-3): 487-498.
[3] KATTO Y. A generalized correlation of critical heat flux for the forced convection boiling in vertical uniformly heated round tubes[J]. International Journal of Heat and Mass Transfer, 1978, 21(12): 1 527-1 542.
[4] BERGLES A E, COLLIER J G, DELHAYE J M, et al. Two-phase flow and heat transfer in the power and process industries[M]. New York: Hemisphere, 1981: 274-278.
[5] CELATA G P, MISHIMA K, ZUMMO G. Critical heat flux prediction for saturated flow boiling of water in vertical tubes[J]. International Journal of Heat and Mass Transfer, 2001, 44(22): 4 323-4 331.
[6] JIAO Bo, QIU Limin, LU Junliang, et al. Liquid film dryout model for predicting critical heat flux in annular two-phase flow[J]. J Zhejiang Univ Sci A, 2009, 10(3): 398-417.
[7] KATAOKA I, ISHII M. Entrainment and deposition rates of droplets in annular two-phase flow[C]∥Proceedings of the ASME/JSME Thermal Engineering Joint Conference. [S. l.]: [s. n.], 1983.
[8] ISHII M, GROLMES M A. Inception criteria for droplet entrainment in two-phase concurrent film flow[J]. AIChE Journal, 1975, 21(2): 308-318.
[9] ZEIGARNIK Y A. Regenerated boiling and enhancement of heat transfer[J]. High Temperature, 2001, 39(3): 447-454.
[10] OKAWA T, KOTANI A, KATAOKA I, et al. Prediction of the critical heat flux in annular regime in various vertical channels[J]. Nuclear Engineering and Design, 2004, 229(2-3): 223-236.
[11] OKAWA T, KITAHARA T, YOSHIDA K, et al. New entrainment rate correlation in annular two-phase flow applicable to wide range of flow condition[J]. International Journal of Heat and Mass Transfer, 2002, 45(1): 87-98.
[12] WALLIS G B. One-dimensional two-phase flow[M]. New York: McGraw-Hill, 1969.
[13] ISHII M, MISHIMA K. Droplet entrainment correlation in annular two-phase flow[J]. International Journal of Heat and Mass Transfer, 1989, 32(10): 1 835-1 846.
[14] GOVAN A H. Phenomenological prediction of critical heat flux[C]∥Proceedings of the 2nd UK National Heat Transfer Conference. [S. l.]: [s. n.], 1988: 315-326.
[15] KOTTOWSKI H M. Sodium boiling[M]. Washington D. C.: Hemisphere, 1981: 813.
[16] ALADYEV I I. The effect of a uniform axial heat flux distribution on critical heat flux with potassium in tubes[C]∥Proceedings of the 4th International Heat Transfer Conference. Paris: [s. n.], 1970.

