熔岩玻璃体核素衰变热功率的计算

包 敏，王群书，师全林，解 峰，王武尚

(西北核技术研究所，陕西 西安 710024)

地下核试验所释放的能量最终转化为热能，提高了爆心温度。核试验瞬间汽化了核装置及部分围岩介质，汽化物质向外膨胀形成爆炸空腔，在空腔冷却过程中，汽化物中难熔性物质首先发生液化，汇集在空腔底部形成熔岩玻璃体，核试验产生的难熔性放射性核素大部分包裹在熔岩玻璃体中。在空腔低于地下水线的情况下，熔岩玻璃体受地下水长期侵蚀作用发生溶解反应，逐渐释放出放射性核素。温度是影响熔岩玻璃体溶解速度的关键因素之一[1]。为评价熔岩玻璃体内核素衰变热功率对温度的影响，需计算核素衰变释热量。地下水在爆后几小时至几天的时间内回流空腔[2]，本文计算核爆10 d后熔岩玻璃体的核素衰变释热量。

1 源项分析

一次地下核试验产生的放射性核素上千种，大部分核素的半衰期极短，很快衰变为半衰期较长的子核或稳态核素。放射性核素活度衰减服从指数规律[3]，10个半衰期后，核素活度衰减为初始值的0.1%，可忽略其放射性衰变释热量。因此计算核爆10 d后的核素衰变热功率需考虑半衰期大于1 d的核素。

为评估FANGATAUFA核试验场的核环境状况，1998年IAEA估算了100 kt TNT当量地下核试验产生的半衰期大于1 a的放射性核素的总活度[4]，给出了这些核素在熔岩玻璃体中的分布比例，根据这些信息可计算出熔岩玻璃体内核素的初始活度(表1)。

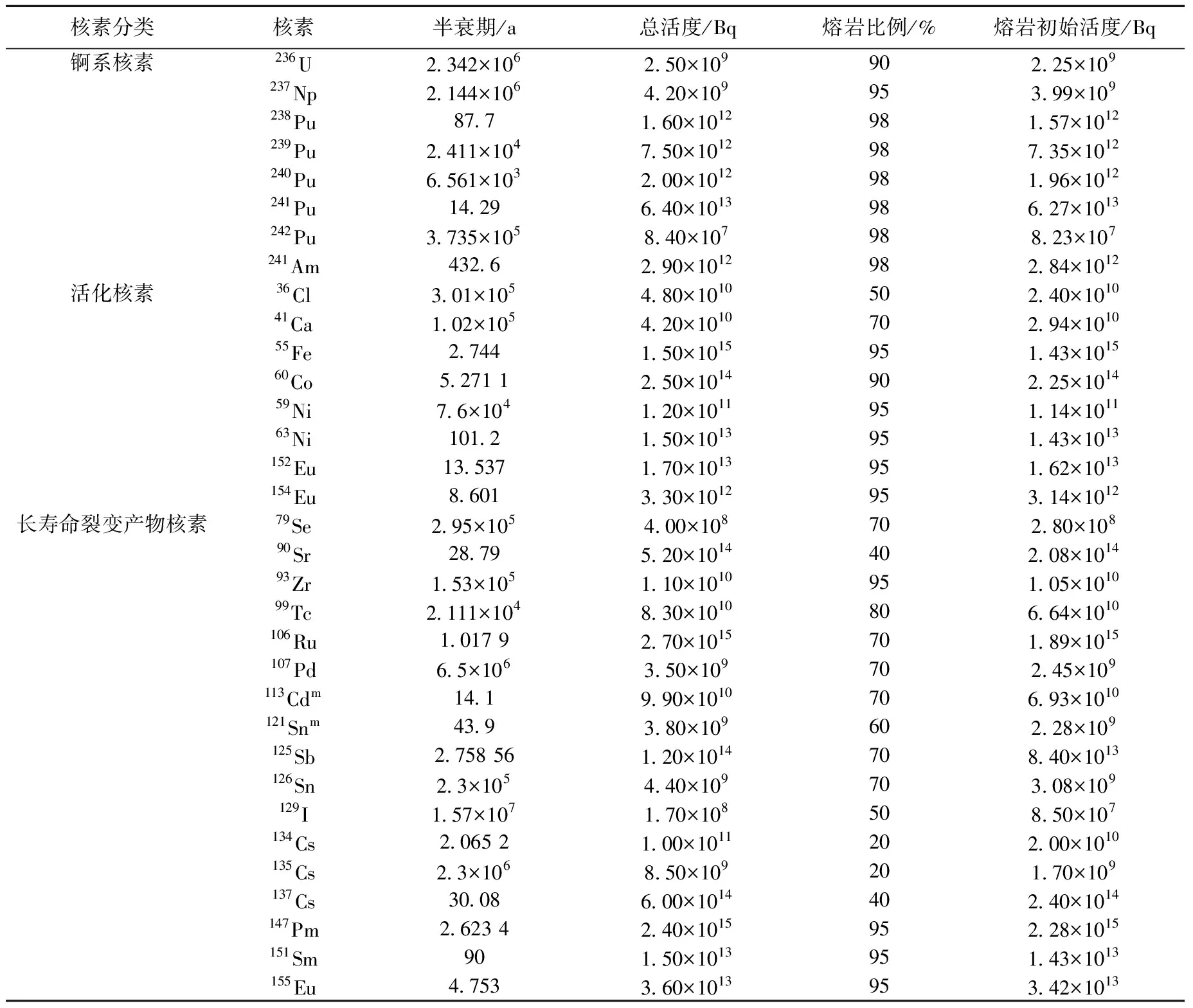
表1 IAEA估算的地下核试验熔岩玻璃体核素活度[4]

半衰期1 d～1 a的放射性核素主要是裂变产物核素，称之为短寿命裂变产物核素。表2列出了累积产额大于0.001的短寿命裂变产物核素，这些裂变产物核素的前驱核的半衰期均很短，远小于1 d，因此核爆10 d后99.9%以上的前驱核衰变为这些裂变产物核素，可采用累积产额估算短寿命裂变产物核素的初始活度。短寿命裂变产物核素的初始总量根据表1中长寿命裂变产物核素的初始总量推算。核试验后裂变产物核素的生成总量与累积产额呈正比，有：

(1)

式中：NA和NB分别为裂变产物核素A和B初始生成的总核数，无量纲；YA和YB分别为核素A和B的累积产额，无量纲。核素的总核数与放射性活度之间满足关系式：

A=λN

(2)

式中：A为核素的放射性活度，Bq；λ为核素的衰变常量，s-1；N为核素的总核数，无量纲。将式(2)代入式(1)，得到：

(3)

已知裂变产物核素A的总活度，由A、B两裂变产物核素的累积产额和衰变常量可推算裂变产物B的总活度。以表1中长寿命裂变产物核素137Cs作为裂变产物核素A，计算表2中各短寿命裂变产物核素的总活度。裂变产物核素的累积产额选用ENDF/B Ⅶ库中的235U在平均能量500 keV中子作用下的累积产额[5]，核素137Cs的累积产额为0.062 2。同一元素各同位素具有相同的物理化学性质，参照表1，表2列出了核素在熔岩玻璃体中的分布比例。

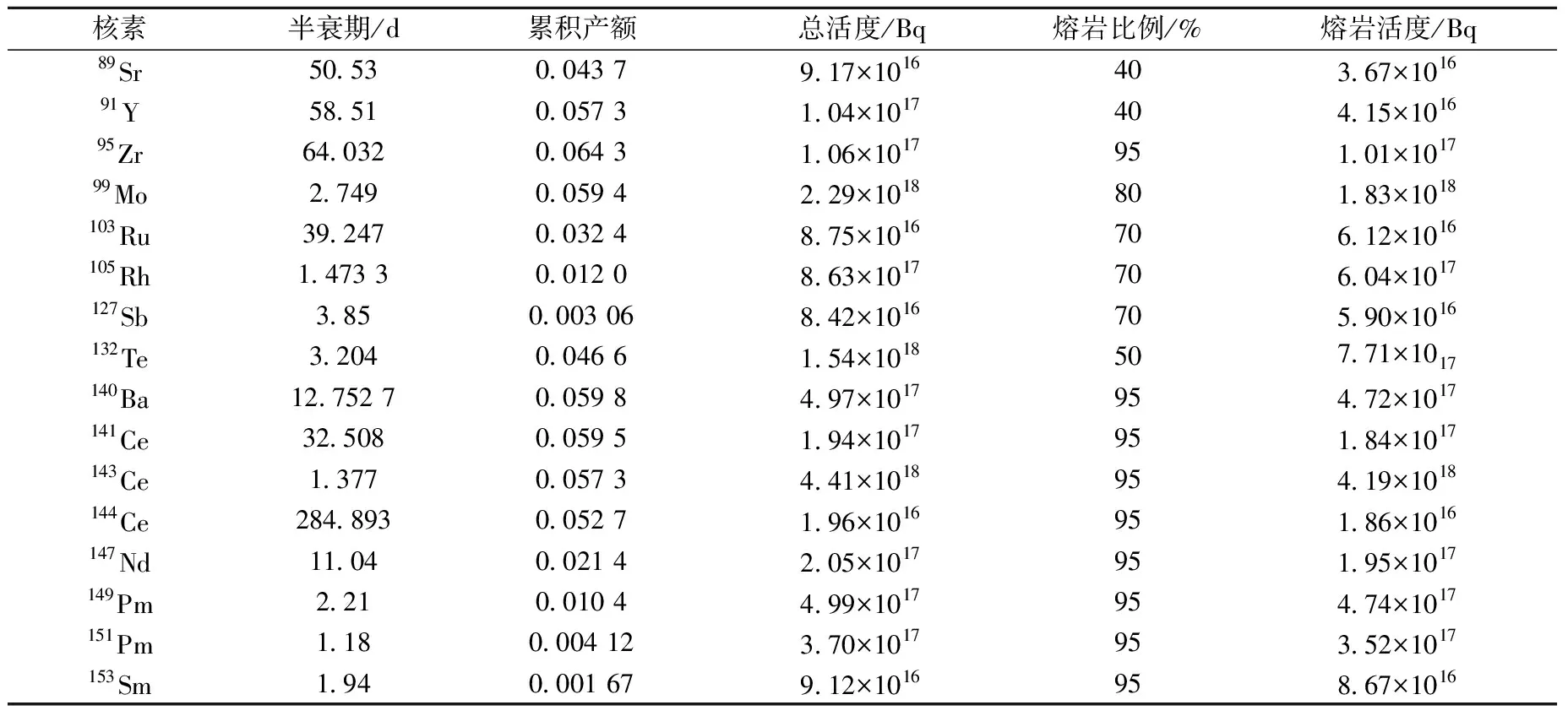
表2 熔岩玻璃体短寿命裂变产物核素含量

2 衰变热功率的计算方法

放射性核素通过向外辐射粒子释放能量，辐射粒子的类型包括α粒子、正负电子、电磁辐射和中微子。熔岩玻璃体的质量和体积均很大。平均1 kt TNT当量地下核试验约产生700 t熔岩玻璃体[1-2]，100 kt TNT当量地下核试验约产生7×107kg熔岩玻璃体。熔岩玻璃体的质量密度约为2.5 g/cm3，对应熔岩玻璃体的体积为2.8×104m3。设放射性核素在熔岩玻璃体内均匀分布，除中微子携带的能量发生逃逸外，其余粒子携带的能量全部沉积在熔岩玻璃体内部，转化为热能。核素衰变热功率采用下式计算：

Hi(t)=1.6×10-16Ai(t)Ei

(4)

式中：Hi(t)为t时刻核素i的衰变热功率，J/s；Ai(t)为t时刻核素i的放射性活度，Bq；Ei为核素i发生一次放射性衰变所释放的除去中微子之外的能量，keV。

2.1 单次衰变

若核素i一次衰变到稳态核，只需考虑核素i的衰变热功率。核素i的放射性活度服从指数衰减规律[3]：

Ai(t)=Ai(0)e-λit

(5)

式中：Ai(0)为核素i的初始活度，Bq；λi为核素i的衰变常量，d-1；t为距初始时刻的时间，d。这类核素及其对应的Ei列于表3，Ei取自ENDF/B Ⅶ库。

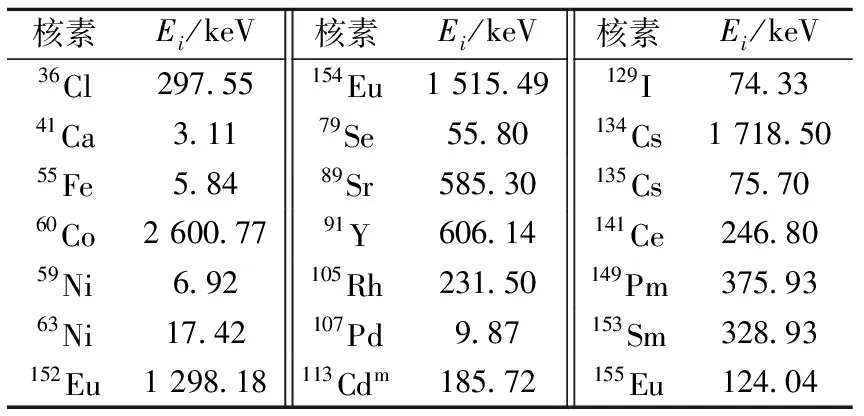
表3 单次衰变核素的衰变热[5]

2.2 级联衰变

有些放射性核素经历若干次级联衰变后最终衰变为稳态核，需计算母核产生的衰变热功率以及各级子核产生的衰变热功率。设母核的初始活度为A1(0)，各级子核的初始活度为0，t时刻母核的活度为A1(t)，1级子核的活度为A2(t)，k-1级子核的活度为Ak(t)，A1(t)采用式(5)计算，A2(t)采用式(6)计算，Ak(t)采用式(7)计算[3]。

(6)

Ak(t)=A1(0)(h1e-λ1t+h2e-λ2t+…+hke-λkt)

(7)

其中：

式中，λ1、λ2、…、λk分别为母核、一级子核、k-1级子核的衰变常量，d-1。表1、2中经历级联衰变的裂变产物核素的母核Ei，子核Ei、衰变方式列于表4。

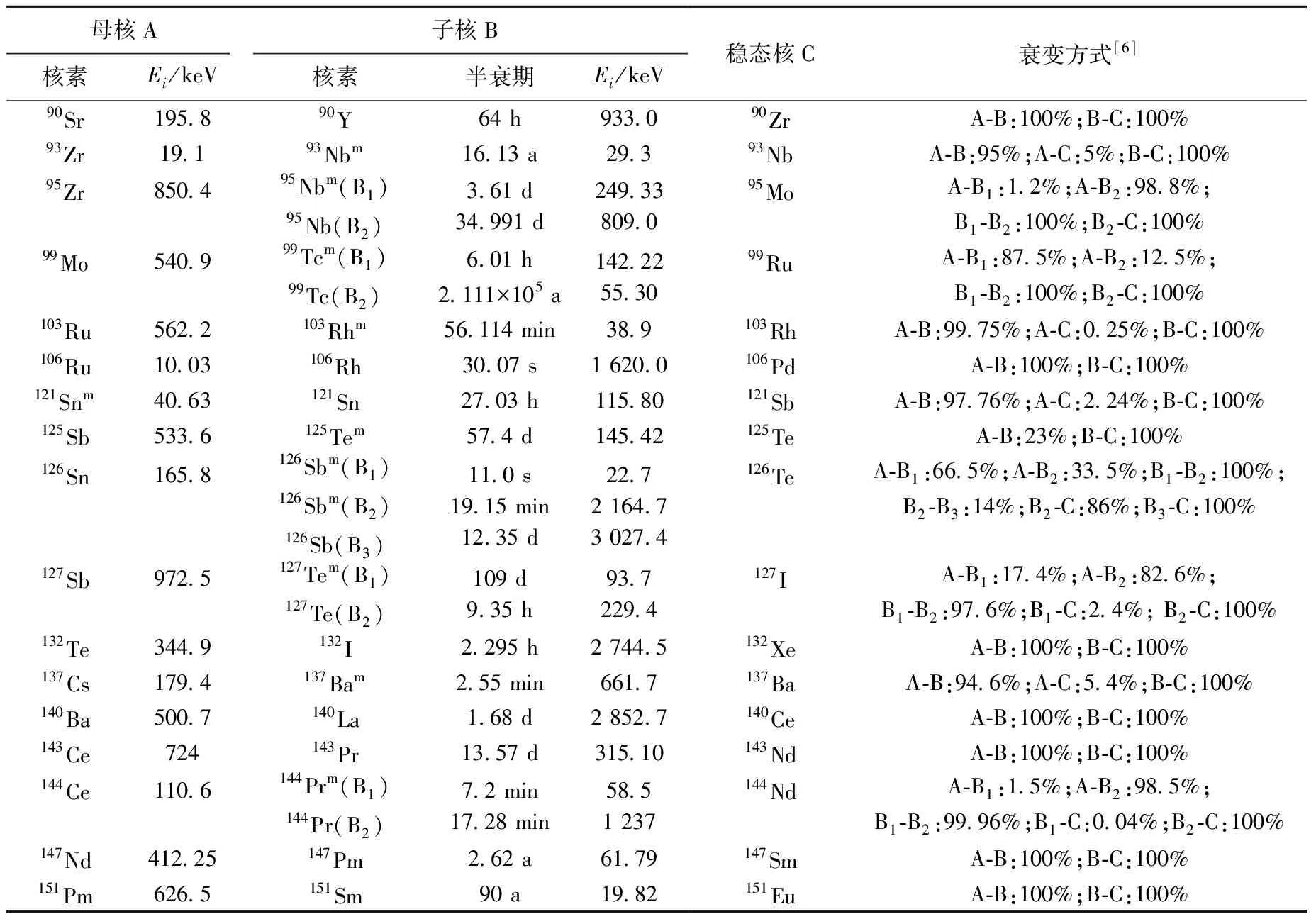
表4 级联衰变裂变产物核素的衰变信息

锕系核素经历多次α衰变和β衰变最终衰变为稳态核素，子核有十几种，按式(7)逐一计算各子核活度非常繁琐。由于在计算时间范围内衰变链尾部子核的活度远小于母核的活度，尾部子核放射性衰变产生的衰变热功率很小，高正明等[7]在计算WgPu材料衰变热功率时只计算每种核素的前1～3次级联衰变热功率。本文采取以下近似措施：在计算时间段内，若某级子核的活度均小于前驱核最高活度的0.1%，则忽略该子核及后续子核的放射性衰变热功率。表5列出锕系核素及其需考虑的各级子核。母核与子核的活度分别采用式(5)、(6)、(7)计算。

表5 锕系核素的衰变信息

3 计算结果

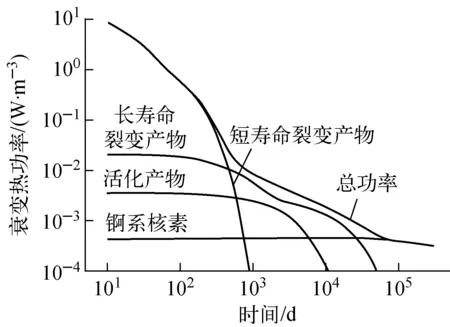
图1 核素衰变热功率计算结果

采用以上方法计算核试验后10～300 000 d时间段内熔岩玻璃体核素衰变产生的热功率，结果示于图1。从图1可见，核素衰变热功率分3个时间段：10～2 000 d、2 000～60 000 d和60 000 d之后。3个时间段内衰变热功率分别近似为直线，说明热功率随时间呈幂函数衰减；各时间段内直线斜率的绝对值依次减小，说明热功率下降速度逐渐变慢。在10～2 000 d阶段，短寿命裂变产物核素的热功率占主要部分，短寿命裂变产物核素的半衰期短，放射性活度衰减快，因此，热功率衰减速度最快。在2 000～60 000 d阶段，长寿命裂变产物核素的热功率占主要部分；60 000 d后锕系元素的热功率占主要部分，锕系元素的半衰期非常长，核素衰变热功率衰减速度很慢。

设熔岩玻璃体的体积比热容为2×106J/(m3·K)，在不考虑热量扩散的情况下，核素每天衰变释放的热量对熔岩玻璃温度的增长量示于图2。

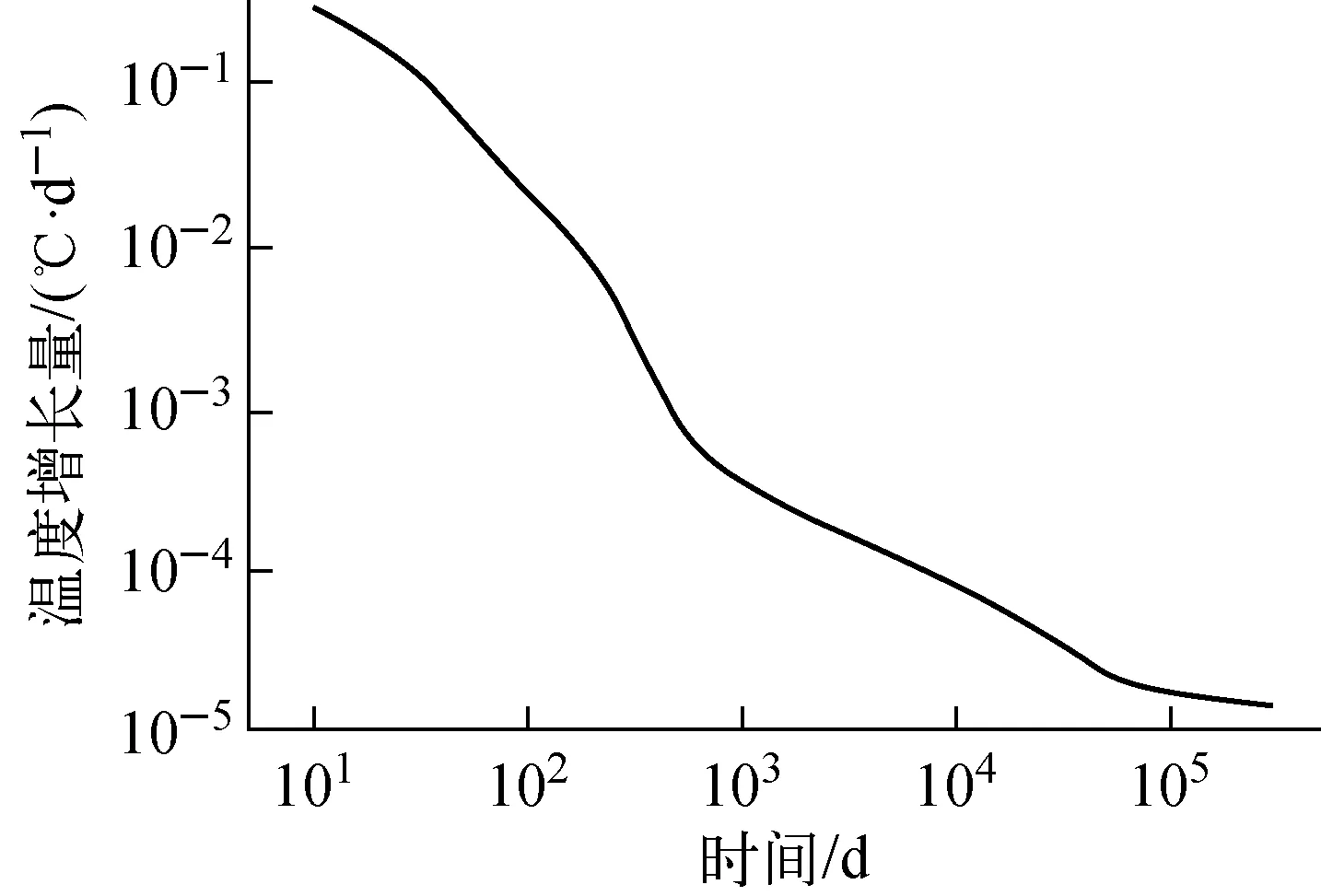
图2 每天熔岩玻璃体温度增长量

根据化学反应动力学公式，温度与熔岩玻璃体溶解速度之间存在以下关系[1，8]：

·

(8)

式中：T1、T2为熔岩的温度，K；L1、L2分别为T1、T2对应的熔岩玻璃体溶解速度，g/(m2·d)；Ea为熔岩玻璃体溶解反应的活化能，cal/mol；R为理想气体常数，1.985 877 5 cal/(mol·K)。熔岩玻璃体的温度为T1，加上核素衰变热功率对熔岩温度的增长量后为T2，通过上式计算核素衰变热功率对熔岩玻璃体溶解速度的相对增长量(L2-L1)/L1(Ea取20 kcal/mol[1]，熔岩玻璃体的温度采用地下核试验场CHESHIRE的熔岩温度的模拟结果[7])，结果列于表6。从表6可知，核素衰变热功率对熔岩温度和玻璃溶解速度的影响不大，且随时间逐渐减弱，1 000 d后影响已非常小。

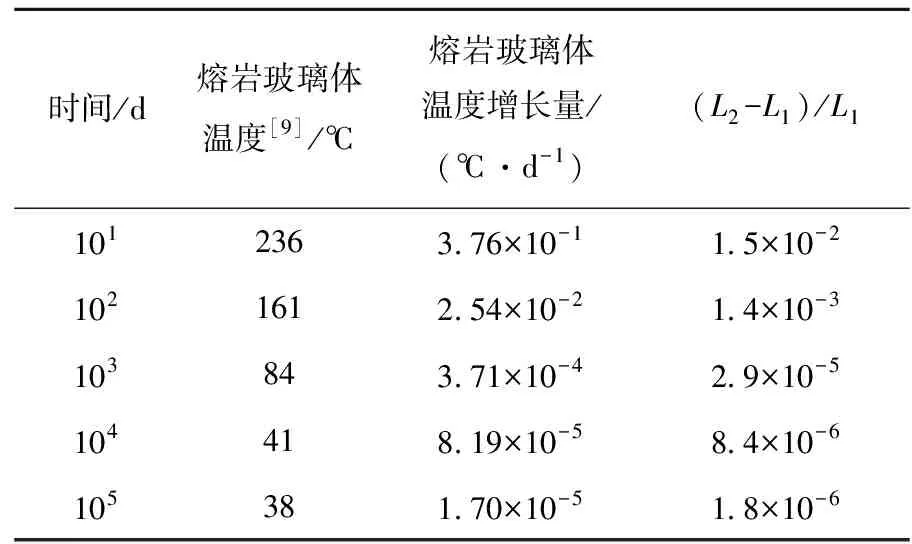
表6 核素衰变热功率对熔岩玻璃体溶解速度的影响

4 结论

综上所述，熔岩玻璃体内核素衰变热功率呈幂函数衰减，且衰减速度逐渐减慢。10～2 000 d，短寿命裂变产物核素衰变热功率占主要部分；2 000～60 000 d，长寿命裂变产物核素热功率占主要部分；60 000 d之后，锕系元素热功率占主要部分。核素衰变热功率对熔岩玻璃体温度和溶解速度的影响不大，且随时间逐渐减弱，1 000 d后影响已非常小。

参考文献：

[1] PAWLOSKI G A, TOMPSON A F B, CARLE S F, et al. Evaluation of the hydrologic source term from underground nuclear tests on Pahute Mesa at the Nevada Test Site: The CHESHIRE test[R]. Livermore: Lawrence Livermore National Laboratory, 2001.

[2] TOMPSON A F B, BRUTON C J, PAWLOSKI G A. On the evaluation of groundwater contamination from underground nuclear tests[J]. Environmental Geology, 2002, 42: 235-247.

[3] 卢希庭，江栋兴，叶沿林. 原子核物理[M]. 北京：原子能出版社，2000：23-25.

[4] IAEA. The radiological situation at the atolls of mururoa and fangataufa technical report, volume 3: Inventory of radionuclides underground at the atolls[R]. Vienna: IAEA, 1998.

[5] HERMAN M, PRITYCHENKO B, SONZOGNI A A. Evaluated nuclear data file (ENDF) retrieval & plotting ENDF/B-Ⅶ.1 library[DB/OL]. 2011[2012-09-01]. http:∥www.nndc.bnl.gov/sigma.

[6] NICHOLS A L. Nuclear data requirements for decay heat calculations[R/OL]. Vienna: IAEA, 2002[2012-03-11]. http:∥ www.ictp.it/～pub_off/lectures/lns020/Nichols/Nichols.pdf.

[7] 高正明，何彬，赵娟，等. 武器级钚材料衰变热功率数值计算与分析[J]. 原子能科学技术，2010，44(2)：240-242.

GAO Zhengming, HE Bin, ZHAO Juan, et al. Numeric calculation and analysis of decay heating power of WgPu[J]. Atomic Energy Science and Technology, 2010, 44(2): 240-242(in Chinese).

[8] 包敏，王群书. 熔岩玻璃体核素239Pu和90Sr释放量的计算[J]. 辐射防护，2013，33(3)：151-157.

BAO Min, WANG Qunshu. Calculation of radionuclides90Sr and239Pu releasing amount from melt glass[J]. Radiation Protection, 2013, 33(3): 151-157(in Chinese).

[9] 包敏，王群书. 地下核试验近场水-热运移数值模拟[J]. 原子能科学技术，2013，47(8)：1 445-1 449.

BAO Min, WANG Qunshu. Water and heat flow simulation after underground nuclear test[J]. Atomic Energy Science and Technology, 2013, 47(8):1 445-1 449(in Chinese).