温度影响下箔片动压止推轴承分析

陈汝刚,陈韬,2

(1.西安交通大学能源与动力工程学院, 710049, 西安; 2.上海电气电站设备有限公司上海汽轮机厂, 200240, 上海)

温度影响下箔片动压止推轴承分析

陈汝刚1,陈韬1,2

(1.西安交通大学能源与动力工程学院, 710049, 西安; 2.上海电气电站设备有限公司上海汽轮机厂, 200240, 上海)

为了探讨高温、高转速透平机械中影响箔片轴承性能的温度及气膜压力场分布等因素,对以弹性支撑结构刚度为常数的箔片动压止推轴承建立了雷诺方程和能量方程,并对轴承内部的气流速度进行了分析;通过将气膜的温度、压力以及箔片的变形进行流固热多场耦合,采用有限差分法进行数值计算,得出了内部气膜温度和压力分布,由此分析了轴承结构刚度和轴承数的变化,以及气膜压力、温度和承载力的变化趋势。研究结果表明:支撑结构刚度增大,轴承间气膜的平均压力减小,平均温度上升;轴承数增大,气膜的平均压力和温度升高。设计气体轴承时弹性支承结构的刚度与转子的转速应予以考虑。

动压;气体轴承;有限差分法;温度;刚度

气体轴承具有高转速、低功耗、无污染、工作温度范围宽等优点,摆脱了液体润滑轴承在转速、温度方面的限制,且应用前景广阔。尽管气体具有较低的黏度,但是在高转速、长时间连续工作的情况下,高温可能导致支撑材料软化,由此影响支撑结构的刚度,进而对承载力造成影响。不仅如此,在高转速或高负载情况下,气膜中不均匀的黏性摩擦也会产生热量而造成局部过热,这种高温、热量的积累问题[1]不能忽视。

1 弹性箔片动压止推轴承的理论分析

弹性箔片动压止推轴承的结构如图1所示,图中顶层箔片底部为刚度均匀的弹性支撑结构。箔片在气膜压力和弹性支撑结构的作用下将发生变形。

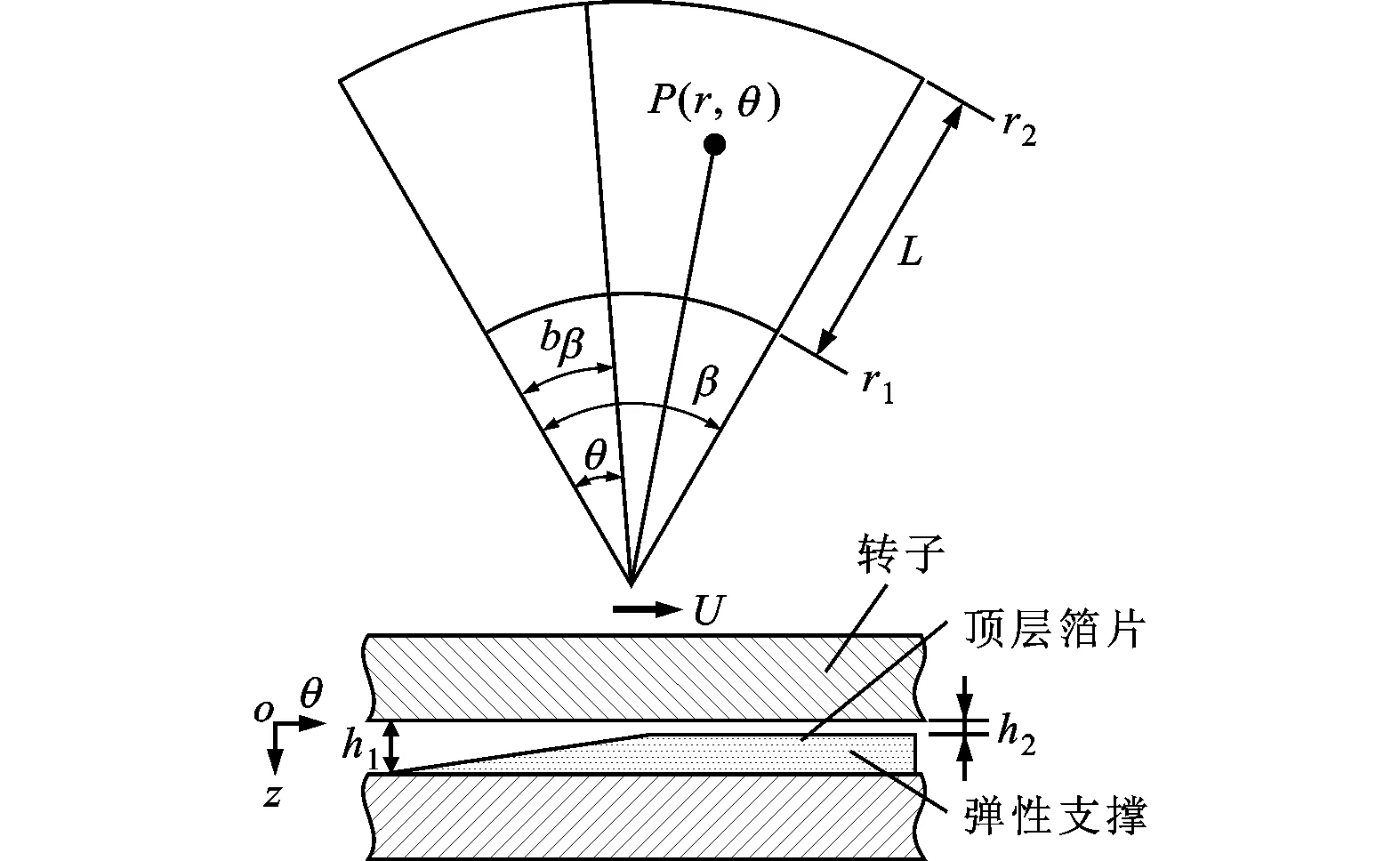
图1 弹性箔片动压止推轴承结构

与液体润滑过程相比较,气体轴承的热量传递或耗散小,但是由于工作转速极高,所以会产生较高的热量而影响轴承的性能。为分析不同刚度和转速下轴承内部的压力和温度状况,在考虑温度的影响下,将雷诺方程和能量方程相结合得

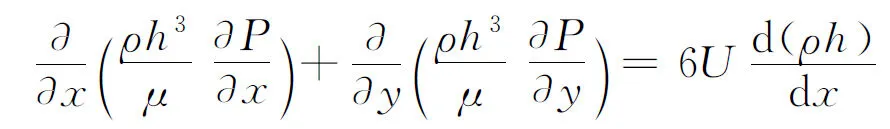
(1)

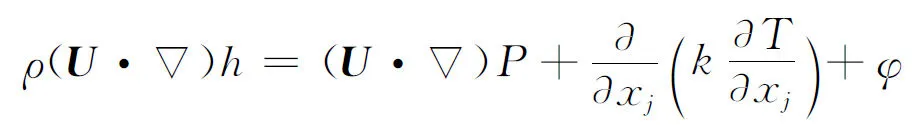
(2)

式中:P为气膜压力;ρ为气体的密度;h为气膜的厚度;μ为气体的动力黏性系数;U为转子的线速度;φ为耗散函数,是流体变形时黏性应力的做功功率。

1.1 压力场分析

将式(1)由直角坐标转换为极坐标时得

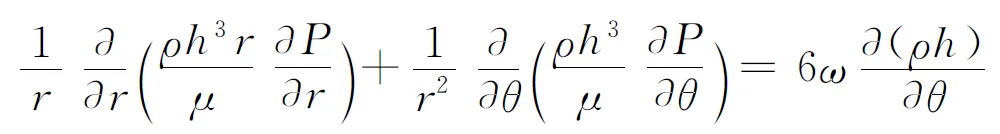
(3)

式中:ω为转子的角速度。

气膜间隙为

h=h2+g(r,θ)+u

(4)

(5)

式中:u为箔片的弹性形变量;g(r,θ)为箔片楔形处增加的间隙厚度;h1、h2分别为气体进入楔形入口和出口的高度;b为节距比;β为单块箔片的张角。

箔片形变为

P-Pa-Ku=0

(6)

式中:Pa为环境压力;K为箔片与支撑结构的刚度。

定义δ=h1-h2,引入无量纲量分别为

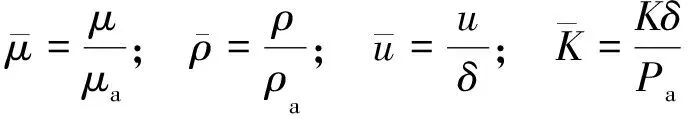
式(1)经无量纲化得

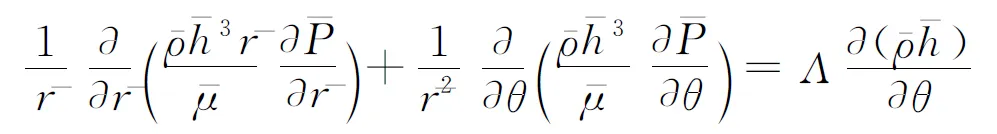
(7)

则箔片形变为

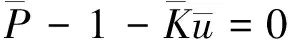
(8)

边界条件为

(9)

1.2 温度场分析

在气体轴承中热量的传递主要有两种方式:热传导和热对流。因热传导相对于对流和黏性产生的热量小,故可以忽略;因气膜厚度极薄,其轴向与径向尺度比极小,故为气膜在轴承间隙中的流动引入活塞流的概念,旨在气膜厚度方向上保持着相同的物理性质。另一方面,将气膜与转子和箔片间的传热量集中到一个单一的变量参数Qs(x,y)中,将其看作内热源项[2],则式(1)可以简化为

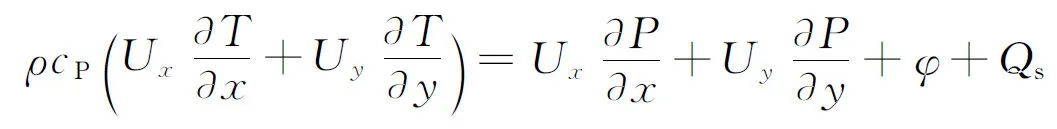
(10)

耗损函数为

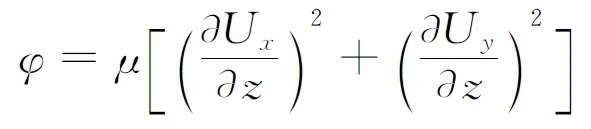
(11)

对能量方程沿气膜厚度方向z积分得

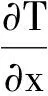
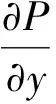
(12)

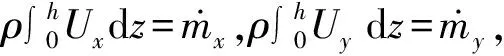
对耗损函数积分得

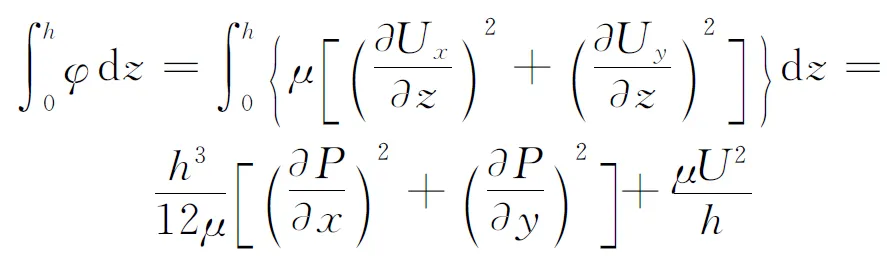
(13)

将式(13)代入式(12)中,并转换为极坐标得

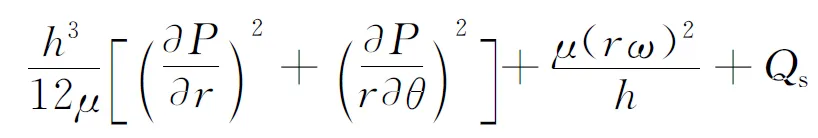
(14)

引入无量纲量分别为

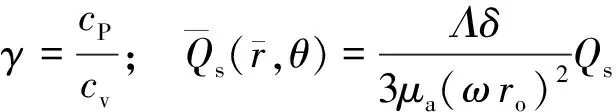
再将式(14)无量纲化得

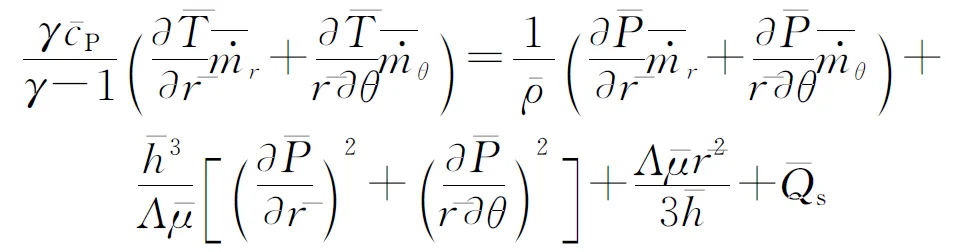
(15)

式(15)的边界条件为

(16)

1.3 轴承内的气流速度分析

模拟流体流动时通常采用连续假设或者分子假设,采用连续假设与否可以通过克努森数Kn来判断,此处计算得出Kn<0.001,故可以采用无滑移边界条件下连续流动来处理[3]。

轴承间隙内的气流速度为

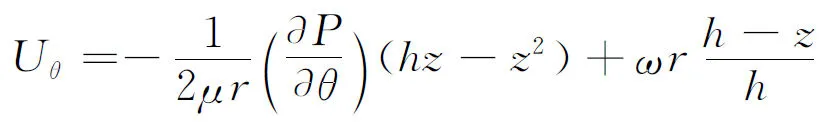
(17)

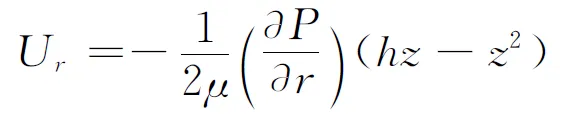
(18)

所以,沿周向的质量流量和沿径向的质量流量分别为

(19)

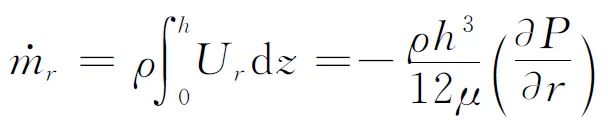
(20)

其经无量纲化得

(21)

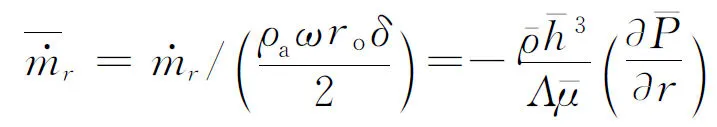
(22)

2 弹性箔片空气动压轴承内流场求解

2.1 程序编制

转子高速旋转时带动流体运动,流体进入转子与轴承之间的楔形区间产生压力,从而使转子浮起,同时在压力的作用下轴承的顶层箔片发生变形,而气膜厚度的变化又会对压力场产生影响。被带动流动的气体在膨胀和压缩时会产生热量,同时转速较高造成的黏性摩擦也会产生较高的热量,由此引起的温度变化又会通过改变气体的物理性质来影响压力,所以说这是一个多重的相互耦合过程。温度、压力耦合计算程序流程如图2所示。

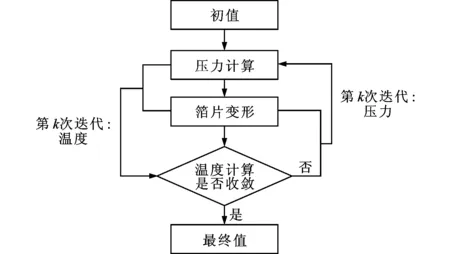
图2 温度、压力耦合计算程序流程

2.2 网格划分

雷诺方程与能量方程的求解采用有限差分法,箔片网格划分如图3所示。压力场和温度场求解时采用相同的网格,这样便于传送节点数值。箔片网格坐标经过转换后如图4所示。

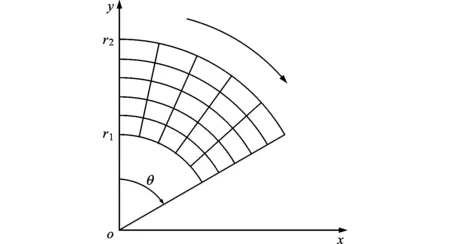
图3 有限差分法计算压力时的网格划分

图4 箔片网格坐标转换后的结果

2.3 气膜压力场求解

采用有限差分法对式(7)离散化,差分项的表达式为

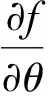
(23)

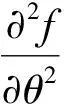
(24)

2.4 气膜温度场求解

对式(15)进行化简得

(25)

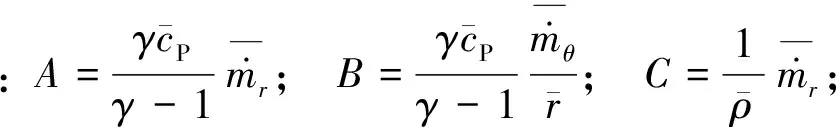
式(25)中,A～G项的值均取第k-1次迭代结果下(i,j)所对应的温度值,压力取第k次的压力计算结果。分别对式(25)中温度和压力的导数项离散,结果见式(23)。

3 结果分析

(1)轴承内部热能主要有:气体压缩和膨胀产生的热能;气体通过自身黏性摩擦转换的热能。气体轴承散热的主要方式有:轴承内气体通过与轴承外冷却气体进行混合;轴承壳体和转子通过与周围环境进行对流换热[4]。

由实验[5]可知,气体轴承产生的热量中75%～85%通过与轴承壳体和转子的对流换热散失掉。所以,本文假设通过良好的散热,压缩膨胀和黏性摩擦产生的80%热量已散失,轴承内部气体温度和压力的分布如图5所示。

(a)平均压力变化

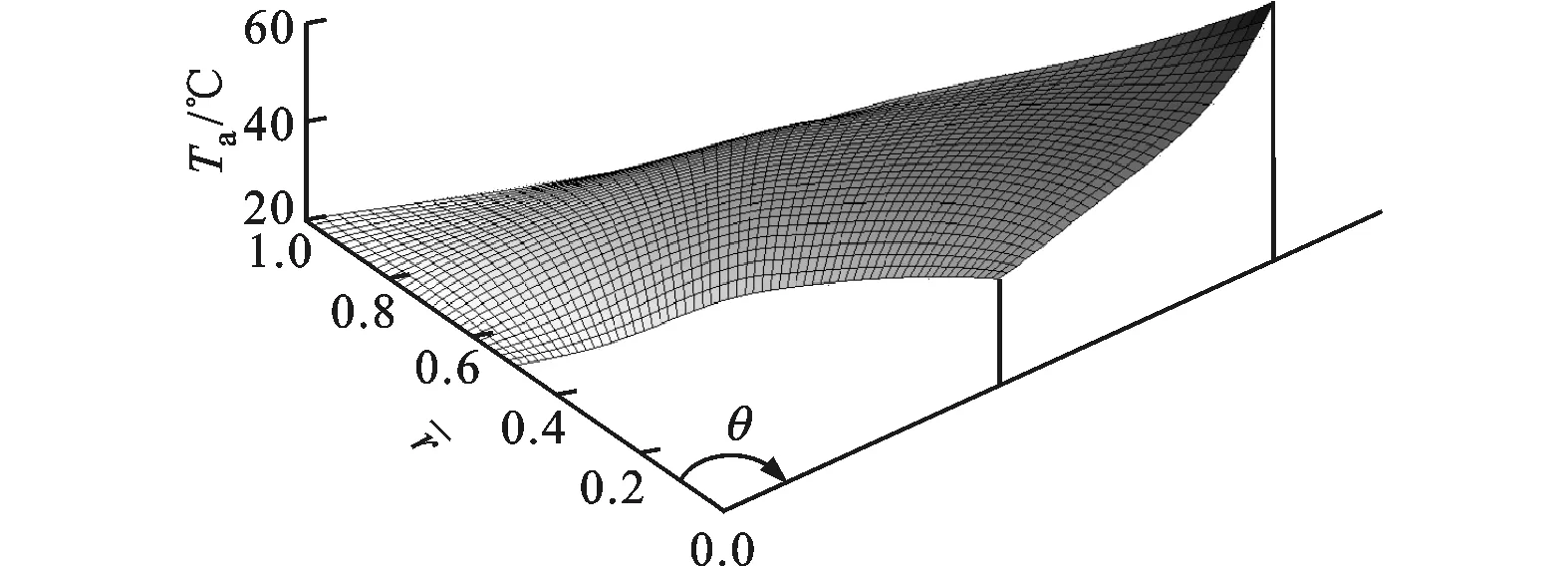
(b)平均温度变化

(2)从图6a可知,在低刚度时,轴承中后部压力较大,造成箔片局部变形较大;随着刚度的增大,轴承中后部压力变化逐渐平缓;随着刚度的继续增大,轴承趋近于刚性轴承,使得最大压力在斜面和平面的交界处。从图6b可知,平均压力随着刚度的增大而增大,随着轴承逐渐接近刚性轴承,刚度增长梯度减小。根据图7,随着刚度的增大,温度逐渐升高。从图8可知,承载力的走势与图6b中平均压力变化相一致。

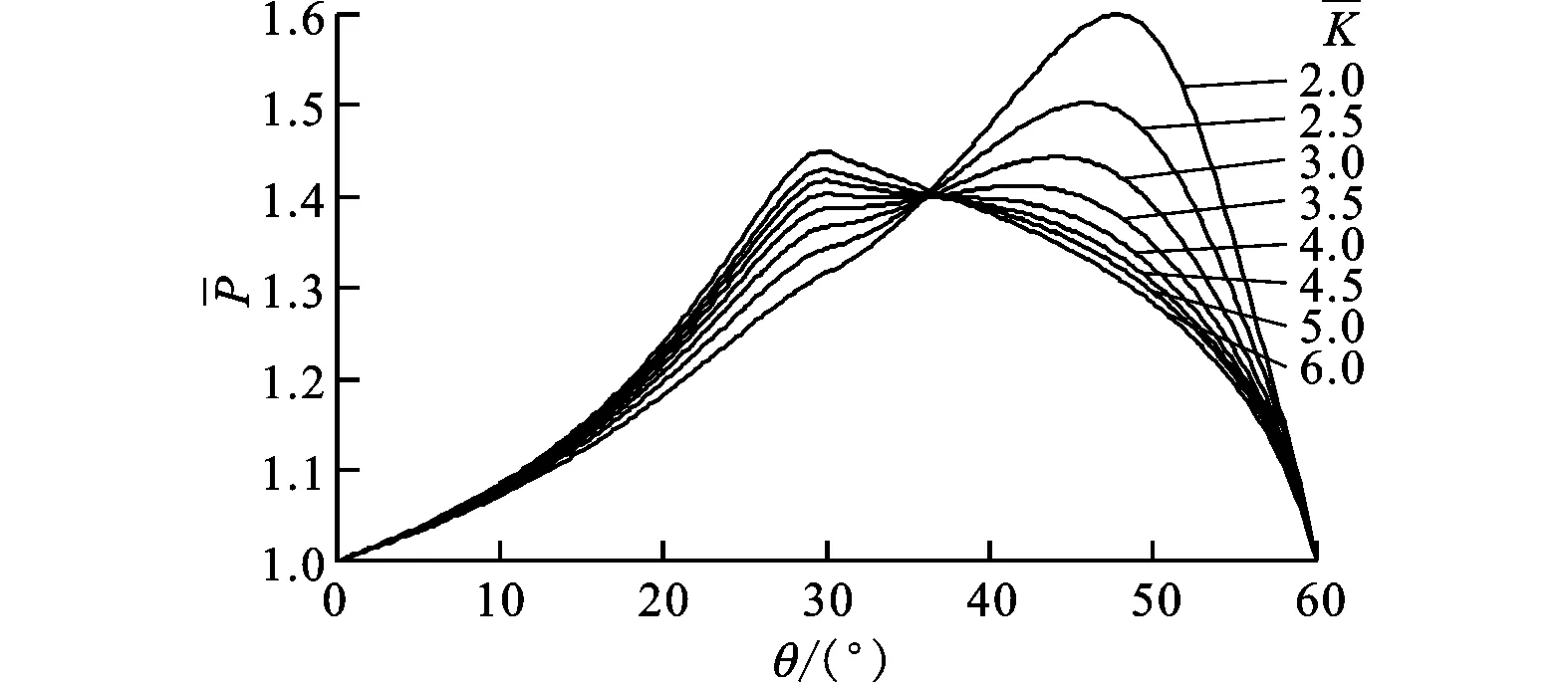
(a)轴承中线处压力变化

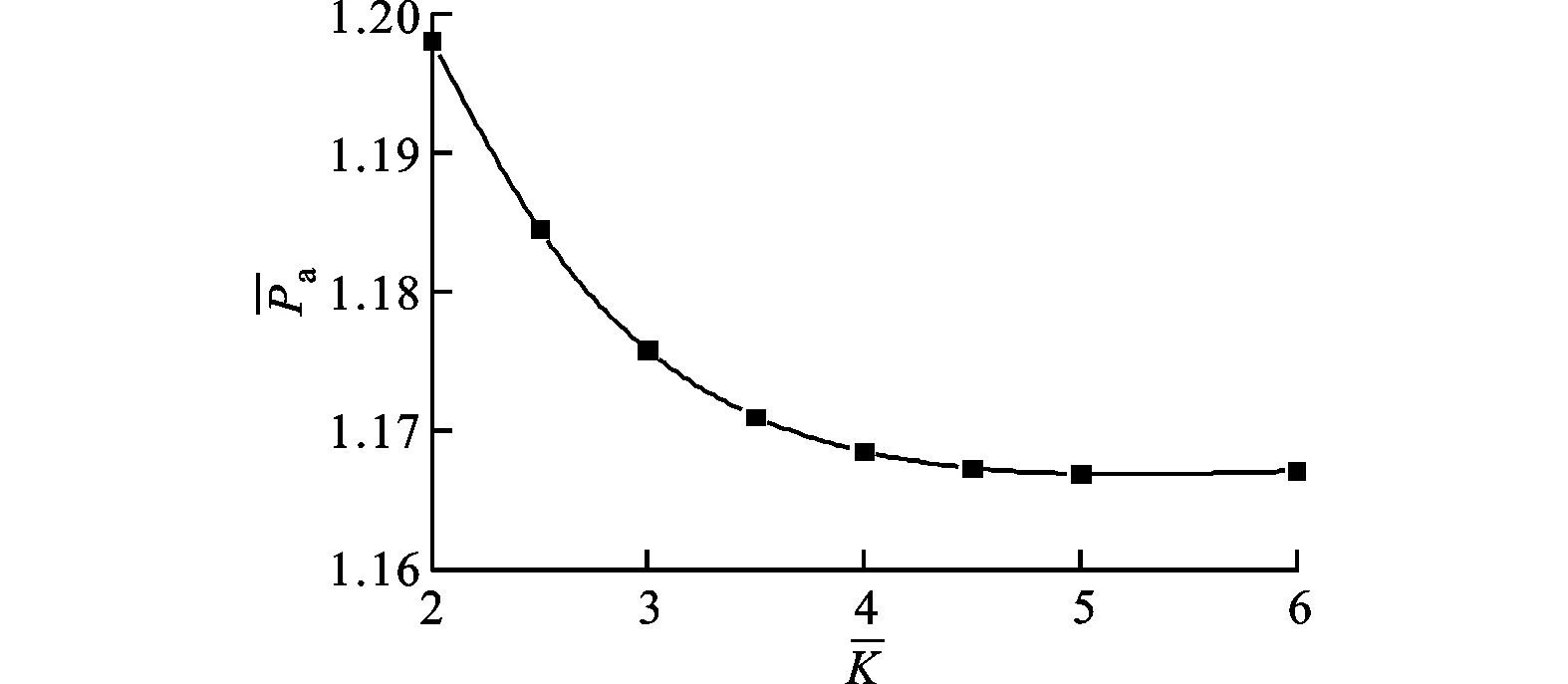
(b)平均压力变化

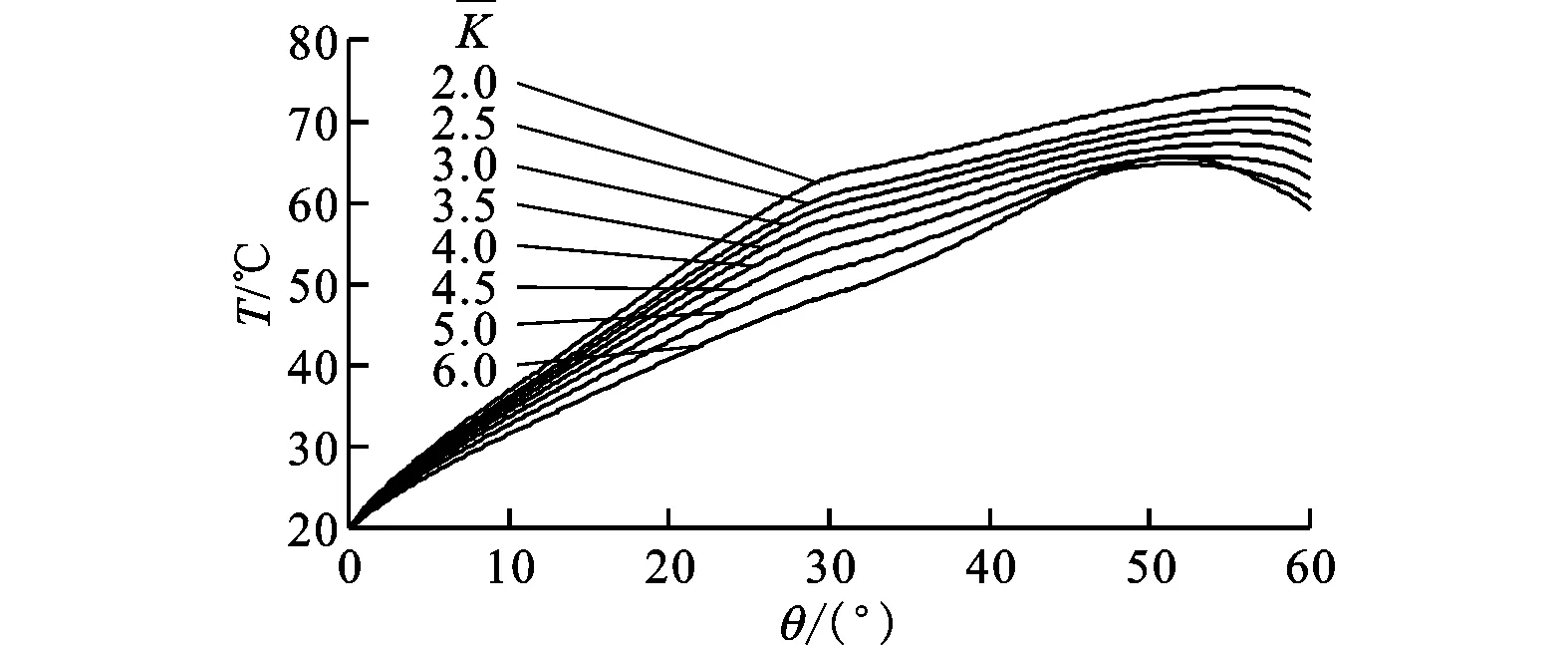
(a)轴承中线处温度变化

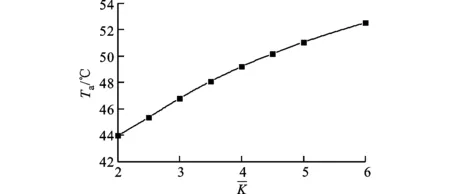
(b)平均温度变化

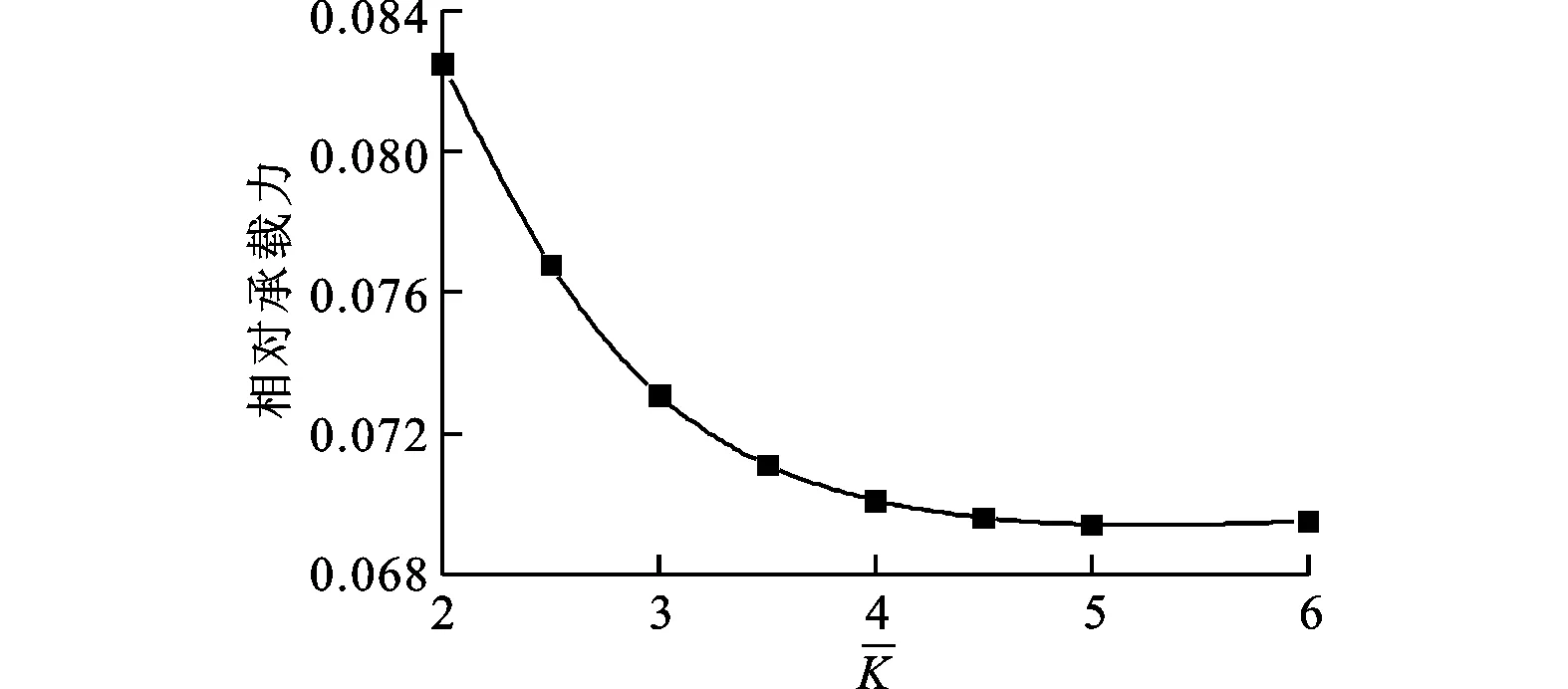
图8 相对承载力随刚度变化

气体轴承设计时需要考虑弹性箔片的刚度,在保证支撑结构不为过度变形失效的情况下,适当地降低刚度要求既可以提高承载力和适应性,又可以降低温度。

(3)从图9可知,轴承数对压力的影响较大,随着轴承数的增加,压力增大且主要在轴承的中后部。在一定的轴承数下,平箔处的压力可以达到均匀分布,超过这一数值后,平均压力和平均温度的增长梯度都会增大,如图10所示。

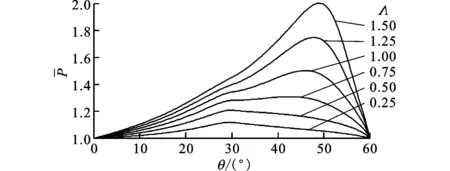
(a)轴承中线处压力变化

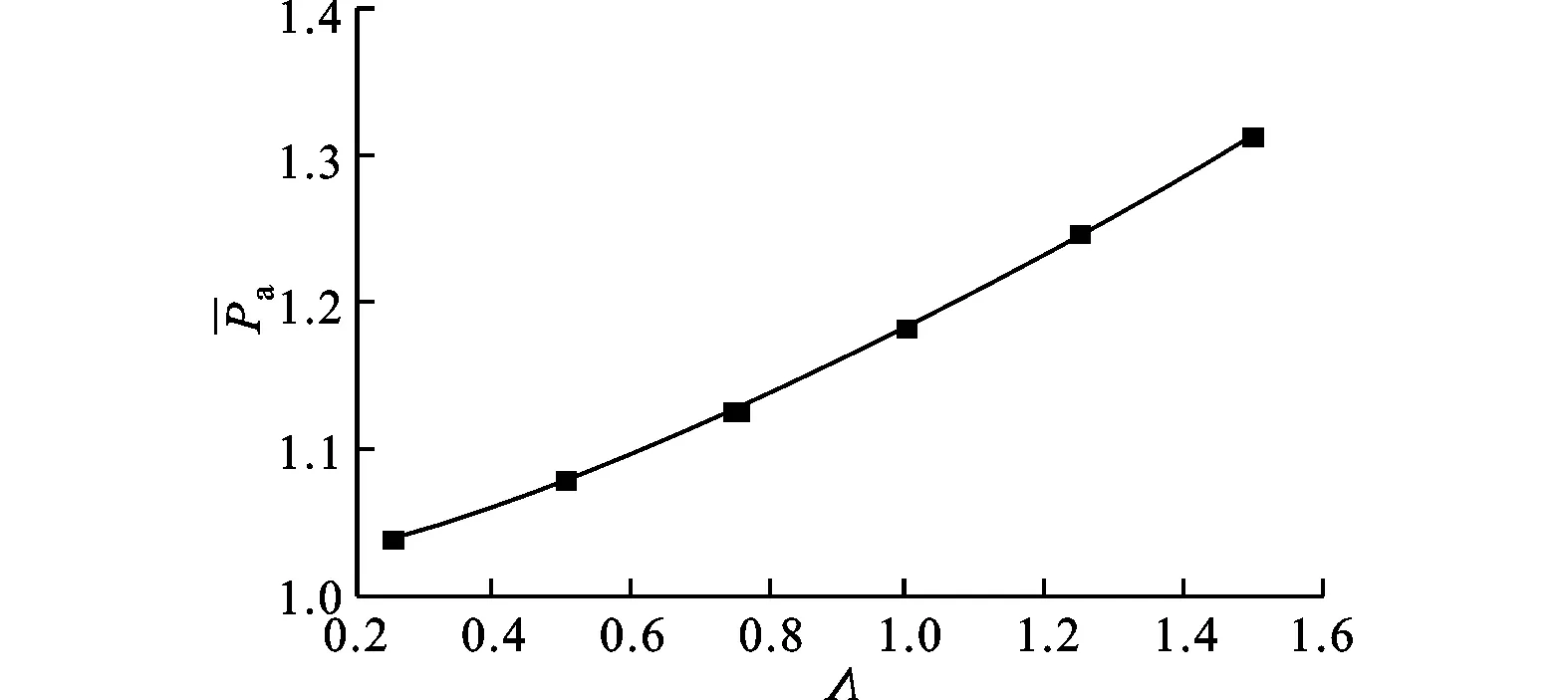
(b)平均压力变化

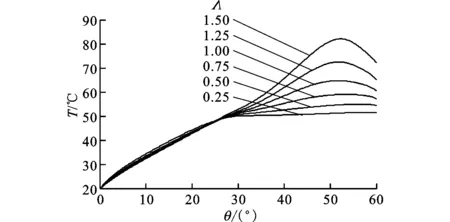
(a)轴承中线处温度变化

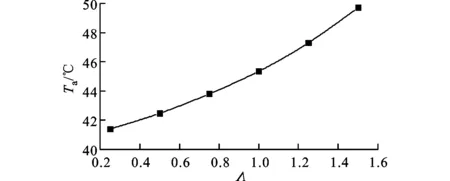
(b)平均温度变化

从图11可知,承载力随轴承数的变化趋势与平均压力变化一致,摩擦力矩与轴承数成正线性相关。

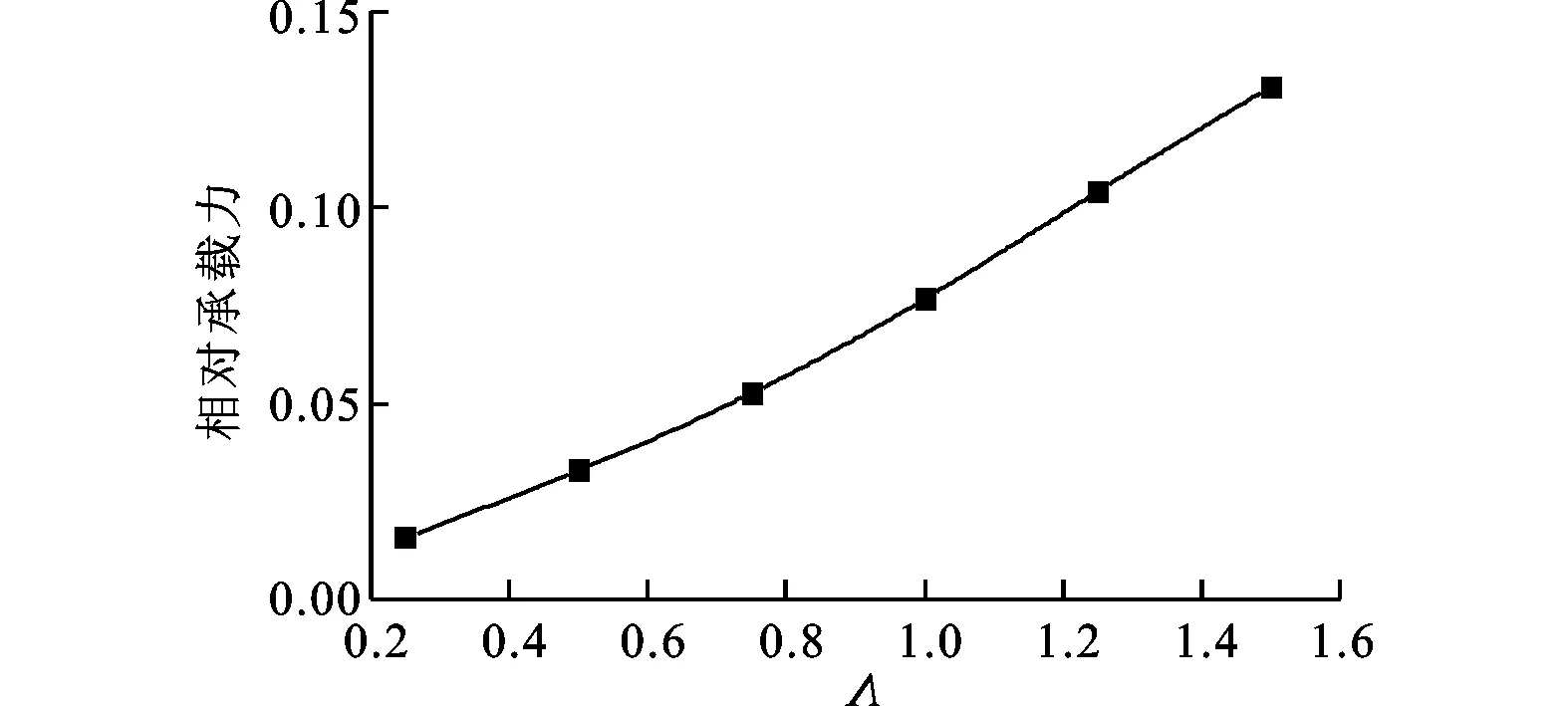
图11 相对承载力随轴承数变化

4 结 论

本文为气体止推轴承建立了热流动力学模型,其中气体润滑介质为可压缩的,其黏性随温度而变化,同时采用有限差分法对气膜的压力、温度和箔片形变进行了耦合求解,得到了气膜压力和温度的三维分布图,以及不同参数对轴承性能影响的走势图,研究结论如下。

(1)气膜的最高温度位于箔片出口端的外径边缘,热量产生的主要原因是黏性摩擦。

(2)在实际运行中,温度过高会造成弹性结构刚度下降,箔片变形增大,气膜压力下降,从而使轴承失效。

(3)转子转速的提高可以增大气膜的平均压力,从而提高轴承的承载力,但是随着转速的进一步提高,气体黏性摩擦会造成温度升高,所以高转速的气体轴承要重视轴承的散热。

(4)支撑结构刚度的下降或者转子转速的提高会使得气膜压力增大,从而造成箔片中后半部的局部区域形变问题凸显,影响轴承的承载性能,所以在进行支撑结构设计时应适当加大该部位的刚度。

[1] PENG Z C, KHONSARI M M.A thermohydrodynamic analysis of foil journal bearings [J].Journal of Tribology, 2006, 128(3): 534-541.

[2] BRUCKNER R J.Simulation and modeling of the hydrodynamic, thermal, and structural behavior of foil thrust bearings [D].Cleveland, Ohio, USA: Case Western Reserve University, 2004.

[3] 虞烈, 戚社苗, 耿海鹏.可压缩气体润滑与弹性箔片气体轴承技术 [M]: 北京: 科学出版社, 2011.

[4] 池长青.气体动静压轴承的动力学及热力学 [M]: 北京: 北京航空航天大学出版社, 2008.

[5] SALEHI M, SWANSON E, HESHMAT H.Thermal features of compliant foil bearings: theory and experiments [J].Journal of Tribology, 2001, 123(3): 566.

(编辑 苗凌)

AnalysisforHydrodynamicFoilThrustBearingsConsideringTemperatureEffects

CHEN Rugang1,CHEN Tao1,2

(1.School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2.Shanghai Turbine Works, Shanghai Electric Power Generation Equipment Co.Ltd., Shanghai 200240, China)

To investigate the influences of pressure and temperature distribution of gas film on the performance of foil bearings applied to turbomachineries at high temperature and speed, the Reynolds equation and the energy equation are established for a hydrodynamic foil bearing with constant stiffness of structural support, and gas velocity in the bearing is analyzed.Coupling the fields of temperature, pressure and deformation of top foil, finite difference method (FDM) is adopted to solve the equations, and pressure and temperature distribution of gas film are obtained.In the analysis, the variation tendency of pressure and temperature of gas is obtained with the changed dimensionless stiffness of support structure and bearing number.It is found that when the dimensionless stiffness of the support structure increases, the gas pressure decreases, however, the gas temperature behaves oppositely, and when the bearing number increases, the pressure and temperature of gas increase, thus the dimensionless stiffness of support structure and bearing number ought to be taken into account in gas foil bearing designing.

hydrodynamic; gas bearing; finite difference method; temperature; stiffness

2014-03-13。

陈汝刚(1970—),男,博士,副教授。

国家自然科学基金资助项目(51076129);中央高校基本科研业务费专项资金资助项目(SYSPZ2011030)。

10.7652/xjtuxb201411006

TH117.21

:A

:0253-987X(2014)11-0032-05