与圆有关的试题分类探究
●
(杭州文海实验学校 浙江杭州 310018)
圆是各地中考和竞赛的重要知识之一,且遍布各种题型,既涉及计算、论证,又涉及探索以及操作题等,考查的知识点侧重于与圆有关的角、计算等.近几年的竞赛或中考试题中,与圆有关的试题在沿袭传统的题型外,还加大了探索、创新的力度,特别是增加了与圆有关的动态问题、圆与代数的综合题等.
在解决与圆有关的问题时,除了要能灵活运用所学知识外,还要注意与其他知识的联系,注意数学思想方法的运用.圆是数学中思想方法比较集中的知识点之一,如转化思想、方程思想、分类思想、整体思想等.本文仅对近几年全国各地区初中数学竞赛及中考中与圆有关的试题进行分类研究,以供参考.
题型1与圆有关的角
圆心角、圆周角、弦切角以及它们的大小与所对(或所夹)弧的度数之间的关系是圆中最基本的数量关系,也是解决与角有关的几何问题的重要知识点,是证明与圆有关结论的常用工具.
例1如图1,在ABCD中,E为对角线BD上一点,且满足∠ECD=∠ACB,AC的延长线与△ABD的外接圆交于点F.证明:∠DFE=∠AFB.
(2014年全国初中数学联赛福建赛区试题)
解在ABCD中,AD∥BC,从而
∠ACB=∠DAF,∠BDC=∠ABD.
因为∠ABD=∠AFD,∠ECD=∠ACB,所以
∠DAF=∠ECD,∠BDC=∠AFD,
于是
△DCE∽△FAD,
因此
由∠BAF=∠BDF,得
△ABF∽△DEF,
故
∠DFE=∠AFB.
点评本题图形比较复杂,关键是根据圆中角的相等关系,并结合平行四边形的性质找出相似三角形,再根据相似三角形的性质判定角的等量关系.圆中角的等量关系给解决图形的相似或全等提供了条件.

图1 图2
题型2垂径定理的应用
圆是轴对称图形,根据这一特征可以得到“垂径定理”这一应用非常广泛的重要定理.利用垂径定理可以解决有关线段长度的计算、比例关系的证明以及其他与圆有关的综合性问题.
例2如图2,点A在半径为20的⊙O上,以OA为一条对角线作矩形OBAC,设直线BC交⊙O于点D,E.若OC=12,则线段CE,BD的长度差是______.
(2012年全国初中数学联赛试题)
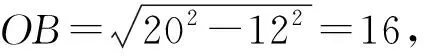
从而
故CE-BD= (EM-CM)-(DM-BM)=
点评对于圆中有关线段长度的计算或比较,垂径定理是常用方法之一.应用垂径定理的关键在于有效利用弦、弦心距和圆的半径(直径)之间的关系,其中勾股定理以及直角三角形的其他性质是解决此类问题的辅助工具之一.
题型3圆的切线
直线与圆的位置关系是圆的重点知识,尤其是直线与圆相切时更具大量有用信息.切线的判定与性质、弦切角与圆周角的关系、切线长定理、圆幂定理等都是竞赛数学的常用知识.

图3

(2011年全国初中数学联赛试题)
解设CE=4x,AE=y,则
DF=DE=3x,EF=6x.
联结AD,BC,因为AB为⊙O的直径,AF为⊙O的切线,所以
∠EAF=90°,∠ACD=∠DAF.
又因为D为Rt△AEF斜边EF的中点,所以
DA=DE=DF,
从而
∠DAF=∠AFD,
于是
∠ACD=∠AFD,
因此
在Rt△AEF中,由勾股定理得
EF2=AE2+AF2,
即
36x2=y2+320.
设BE=z,由相交弦定理得
CE·DE=AE·BE,
即
yz=4x·3x=12x2,
从而y2+320=3yz.
(1)
由AD=DE,得
∠DAE=∠AED,
又∠DAE=∠BCE,∠AED=∠BEC,从而
∠BCE=∠BEC,
于是
BC=BE=z.
在Rt△ACB中,由勾股定理得
AB2=AC2+BC2,
即
(y+z)2=320+z2,
从而y2+2yz=320.
(2)
联立式(1)和式(2),解得y=8,z=16,故
AB=AE+BE=24.
点评“切线与经过切点的半径垂直”这一性质可以将切线与直角联系起来,将圆的问题与直角三角形联系起来.切线的性质、勾股定理的应用和方程思想是本题的主要考查内容.
题型4四点共圆
四点共圆有3个性质:(1)共圆的4个点所连成同侧共底的2个三角形的顶角相等;(2)圆内接四边形的对角互补;(3)圆内接四边形的外角等于内对角.这3个性质提供了圆中角之间的数量关系,为解决与角有关的计算或证明提供了条件.
例4设△ABC的外心、垂心分别为O,H,若点B,C,H,O共圆,则对于所有的△ABC,求∠BAC所有可能的度数.
(2013年全国初中数学联赛试题)
解分3种情况讨论:
(1)如图4,若△ABC为锐角三角形,则
∠BHC=180°-∠A,∠BOC=2∠A.
由∠BHC=∠BOC,得
180°-∠A=2∠A,
于是
∠A=60°.

图4 图5
(2)如图5,若△ABC为钝角三角形,则
①当∠A>90°时,∠BHC=180°-∠A,∠BOC=2(180°-∠A),由∠BHC+∠BOC=180°,得
3(180°-∠A)=180°,
于是
∠A=120°.
②当∠A<90°时,不妨设∠B>90°,则
∠BHC=∠A,∠BOC=2∠A.
由∠BHC+∠BOC=180°,得
3∠A=180°,
于是
∠A=60°.
(3)若△ABC为直角三角形,则
①当∠A=90°时,因为O为边BC的中点,B,C,H,O不可能共圆,所以∠A不可能等于90°.
②当∠A<90°时,不妨设∠B=90°,此时点B与点H重合,于是总有B,C,H,O共圆,因此∠A可以是满足0°<∠A<90°的所有角.
综上可得,∠A所有可能取到的度数为所有锐角及120°.
点评分类讨论是本例的重要思想方法,分类之后图形中根据四点共圆得到角与角之间的数量关系是解决本题的基础知识.
题型5三角形的内切圆
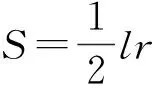
例5在△ABC中,AB=7,BC=8,CA=9,过△ABC的内切圆圆心I作DE∥BC,分别与AB,AC相交于点D,E,则DE的长为______.
(2013年全国初中数学联赛试题)
解如图6,设△ABC的3条边长为a,b,c,内切圆I的半径为r,边BC上的高为ha,则
从而
因为△ADE∽△ABC,所以
于是
点评本题主要通过三角形面积的不同计算方法推导出三角形高与内切圆半径的关系,然后利用相似三角形的比例关系得到未知线段与已知线段之间的数量关系,从而求解.

图6 图7
题型6圆与圆的位置关系
2个圆的位置关系问题一般都是通过辅助线进行转化.圆的基本性质、直线与圆的位置关系等知识在2个圆问题中的应用极为广泛,相切2个圆经过切点的公共切线,相交2个圆的公共弦以及联结2个圆心的直线是常用的辅助线.
例6如图7,⊙O的直径为AB,⊙O1过点O,且与⊙O内切于点B,C为⊙O上的点,OC与⊙O1交于点D,且OD>CD.点E在OD上,且DC=DE,BE的延长线与⊙O1交于点F,求证:△BOC∽△DO1F.
(2012年全国初中数学联赛试题)
证明联结BD.因为OB为⊙O1的直径,所以∠ODB=90°.又因为DC=DE,所以△CBE是等腰三角形.
设BC与⊙O1交于点M,联结OM,则∠OMB=90°.又OC=OB,从而
∠BOC= 2∠DOM=2∠DBC=
2∠DBF=∠DO1F,
而∠BOC,∠DO1F分别是等腰△BOC、等腰△DO1F的顶角,故△BOC∽△DO1F.
点评分别在2个圆中应用圆周角的性质、等腰三角形的性质,尽可能地将角的等量关系挖掘出来,为证明三角形相似提供足够的条件.
题型7与圆有关的比例线段
圆中有关等积式、等比式及混合等式等问题主要与圆的相交弦定理、切割线定理以及三角形的相似等知识相关.这类问题难度较大,在中考中不常出现,但在数学竞赛中仍作为常考内容出现.
例7如图8,PA为⊙O的切线,PBC为⊙O的割线,AD⊥OP于点D.证明:AD2=BD·CD.
(2012年全国初中数学联赛试题)
证明联结OA,OB,OC.因为OA⊥AP,AD⊥OP,所以由射影定理,得
PA2=PD·PO,AD2=PD·OD.
由切割线定理,得
PA2=PB·PC,
从而
PB·PC=PD·PO,
于是点D,B,C,O共圆.
由∠PDB=∠PCO=∠OBC=∠ODC,∠PBD=∠COD,得
△PBD∽△COD,
从而
故
AD2=PD·OD=BD·CD.
点评要证明乘积式,一般将乘积式转化为比例式,然后将比例式中的4条线段组成相似三角形即可.如果线段不能组成三角形,就想办法找等量关系,将其中的一条或几条线段替换,再确定相似三角形.

图8 图9
题型8与圆有关的综合题
圆作为初中数学的重要内容之一,在中考中也常常以综合题的形式出现.这类问题一般以圆为问题背景,综合了几何和代数的大量知识点,融合了分类讨论、数形结合、转化化归、方程函数等重要数学思想方法,全面考查学生分析问题、解决问题的能力.

(1)求∠COB的度数.
(2)求⊙O的半径R.

(2012年浙江省杭州市数学中考试题)
解(1)因为AE切⊙O于点E,所以
AE⊥CE.
由OB⊥AT,得
∠AEC=∠CBO=90°,
又∠BCO=∠ACE,从而
△AEC∽△OBC.
因为∠A=30°,所以
∠COB=∠A=30°.

即
EC=AE·tan30°=3.


在△COB中,∠BOC=30°,即
从而
于是
又OC+EC=OM=R,得
整理得
R2+18R-115=0,
即
(R+23)(R-5)=0,
解得R=5或R=-23(舍去).故R=5.

图10
(3)在EF的同一侧,△COB经过平移、旋转和相似变换后,2个顶点分别与点E,F重合的三角形有6个(如图10所示).
如图9,延长EO交圆O于点D,联结DF.因为EF=5,直径ED=10,所以∠FDE=30°,从而
则
点评本题综合性较强,重点考查了切线的性质、垂径定理、勾股定理、相似三角形的判定与性质、含30°直角三角形的性质、平移及旋转的性质以及锐角三角函数定义.
与圆有关的竞赛题或中考题题型丰富,本文只就几类问题举一些典型例子来说明如何有效利用圆的基本性质、直线与圆、圆与圆的关系及性质来充分挖掘问题条件与结论之间的关系,以达到解决问题的目的.

