一道中考格点题解法探求
●
(温州第十七中学 浙江温州 325028)
格点题是浙江省湖州市近几年数学中考试题的一大特色,其在数学探究性学习方面有着积极的导向作用,试题本身也具有较高的研究价值.笔者撷选2013年浙江省湖州市数学中考试题中的格点题与大家共赏.

图1
原题呈现
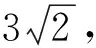
( )
A.7 B.14 C.24 D.28
(2013年浙江省湖州市数学中考试题)
1 解法举例
1.1 构图法
在解决问题之前先来研究抛物线上横坐标间距相同的点的纵坐标所具有的特征.
引理
点(xi,yi)(n取正整数)是二次函数y=ax2+bx+c(a≠0)图像上的点,若有x2-x1=x3-x2=x4-x3=…=xi+1-xi=…=d,设Δyi=yi+1-yi,则Δyi+1-Δyi=2ad2.
证明Δyi+1-Δyi= (yi+2-yi+1)-(yi+1-yi)=

(xi+2-xi+1)[a(xi+2+xi+1)+b]-(xi+1-xi)[a(xi+1+xi)+b]=
d[a(xi+2+xi+1)+b-a(xi+1+xi)-b]=
d[a(xi+2-xi+1)+a(xi+1-xi)]=d(2ad)=2ad2.
特别地,当d=1时,Δyi+1-Δyi=2a,即当横坐标每增加1个单位时,纵坐标的增量每次增加2a,是一个定值[1].
再看试题,如图2,先研究过点O(0,0),D(3,3)的开口向下且顶点也落在格点上的抛物线,可分成2类讨论:
(1)当抛物线与OB的2个交点位于对称轴的2侧时(以点O,D为例),此时对称轴有2种可能:

①对称轴为直线x=1.如图2作出点D与O关于直线x=1的对称点D′和O′,则DD′>OO′,这与抛物线开口向下矛盾,因此,以直线x=1为对称轴,过点O(0,0),D(3,3)的开口向下且顶点也落在格点上的抛物线不存在.
②对称轴为直线x=2.如图3所示,设此时过点O,D,D′,O′的顶点为格点、开口向下的抛物线的顶点为E(2,k),则它们的纵坐标如表1所示:

表1 格点O,D,E,D′,O′的对应值
由引理可知,k-6=6-2k,解得k=4,其中二阶增量2a=-2,于是a=-1,此抛物线方程为y=-(x-2)2+4.

(2)当抛物线与OB的2个交点位于对称轴的同侧时(仍以点O,D为例).
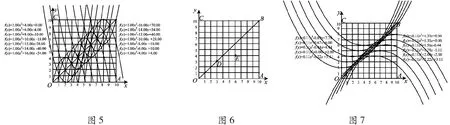
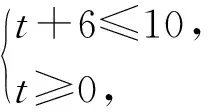
综合(1)(2)可知符合题意的抛物线共有24条.故选C.
1.2 待定系数法
假设符合试题条件的抛物线顶点坐标为(-m,k),则抛物线解析式为y=a(x+m)2+k.以过点O,D的抛物线为例,将O(0,0),D(3,3)代入,得y=a(x+m)2+k,从而


通过计算可得符合题意的t和(-m,k)对应值如表2所示:

表2 t和(-m,k)的对应值
由表2可知,符合条件的抛物线条数为2+3+3+4+4+3+3+2=24.故选C.
2 解后语
本题既可以通过形的特征来构图解决,也可以利用数的角度分析求解,2种解法各有特色.第1种解法利用构造基本图形法来求解需要了解“引理”这一性质,学生在利用构造图形解题时常忽视2个与OB的交点位于对称轴同侧这种类型,往往容易错选成B;第2种解法可以避免按对称轴分类不全的情况,同时也不需要“引理”的铺垫,但计算较为繁杂,如果中考中不允许使用计算器,较浪费时间;在允许使用计算器的地区,学生可以利用计算器的函数生成数字表格功能进行列表.此外,也可以将2种解法结合解决本题,如先用解法2分析出经过点O,D的抛物线,再按解法1的方法构造出基本图形,结合平移等方法亦可分析出正确结果.总体而言,本题在中考中对学生函数与格点综合分析能力要求较高,而作为课外探究学习素材更有利于提高学生的数学分析能力,拓宽学生问题解决的视野.
参 考 文 献
[1] 叶茂恒.一道中考题解法新探[J].中学数学教学参考:中旬,2010(6):57-58.

