优化的梯度最短路径骨架提取算法
杨晨晖,刘 聪
(厦门大学信息科学与技术学院,福建 厦门 361005)
骨架的概念最早是由Blum在1967年提出的,当时他称骨架为“中轴”(medial axis)[1],Blum还分别给出了2种骨架典型定义[1-2].二维图像的骨架提取方法大体可分为4大类:
1) 基于拓扑和几何分析的方法;2) 细化的方法;3) 基于距离场的方法;4) 基于广义势场的方法.这些方法提取的结果依然不理想,主要表现在骨架的不稳定性和骨架的连通性方面,Bai等[3]引入边界离散曲线演化(discrete curve evolution)在保证骨架连通性的前提下,剪除对视觉不重要的骨架分枝;Golland等[4]利用物体模型的拓扑先验知识,提出用固定拓扑骨架(fixed topology skeleton)来减少骨架的冗余分枝,消除骨架的不稳定性.Choi等[5]引入尺度因子,提出距离场内基于连续准则的骨架提取算法,在一定程度上解决了骨架的连通性问题;丁颐等[6]提出一种基于种子生长的方法来连接断裂的骨架.
本文引入刘俊涛等[7]提出的梯度最短路径的算法,得到连通的、准确的物体模型骨架,并在此基础上提出基于梯度的优化方法,大大地减少了程序运行的时间.
1 基于距离变换的梯度最短路径算法
1.1 图像梯度
本文利用欧氏距离变换对二值化的人体图进行距离变换,然后利用一阶微分形象化的定义,在行和列方向上各自构建一个简单的3×3算子(如图1所示),计算图像的梯度.
图1 自定义的行方向和列方向上的算子
Fig.1 Custom operators in the row and column
如图2(c)可知,距离变换(DT)的梯度图(|DT|)突出显示了图2(b)中灰度值变化比较显著像素点(图2(c)中前景点中黑色的部分).实际这些像素点的集合已经组成了原人体图的中脊线.由于梯度化的结果也突出模型轮廓边缘的像素点,很难用阈值来消除非脊点的影响;即使消除这些影响,提取出的骨架也难以保证单像素性和连通性.因此单纯依靠梯度图来获取模型的骨架不能满足要求.

图2 二值化人体、距离变换、梯度和局部极大值点示意图Fig.2 The binary image of human body, the image of distance transformation, the grads image, the local maximum points image
1.2 关键点
设p是物体A内的任意一个像素点(或体素点),表示p点的距离变换值,S是点p邻域点组成的集合.对任意的像素点(或体素点),都有DT(q)≤DT(p),则称p为物体A的距离变换局部极大值点[7].
本文是基于8邻域搜索得到的距离变换局部极值点.
观察图2(b)发现,潜在骨架点的距离变换值应该比邻域的距离值大.因此通过寻找距离图中的局部极大值点,可以得到潜在的骨架点.如图2(d)所示,粗点表示距离变换图的局部极大值点,而且可以看到,局部极大值点全部落在梯度图的脊线上.
由于最短路径算法是按照梯度方向连接每个骨架点,局部极大值点必然会在最长的连接曲线上.利用这一性质,本文用一个极大值点来取代连通的所有局部极大值点,称这一替代的极大值点为关键点.关键点是连通的局部极大值点中梯度最小的那一个像素点(体素点)[7].
易知,关键点也是局部极大值点,所以关键点都坐落在梯度图的脊线上,可以认为这些关键点是物体骨架的一个子集.之后的工作就是寻求一种方法把这些关键点按照梯度的方向连接起来,得到物体的曲线骨架.
1.3 基于梯度的最短路径
本文采用的最短路径算法是迪杰斯克拉(Dijkstra)算法.根据该算法的需要,必须根据梯度图中的像素点来构建邻接矩阵.
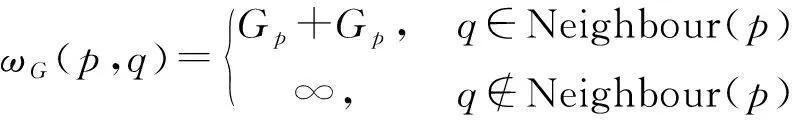
因此可以根据梯度权的定义,来构建图像的一个无向图和邻接矩阵.值得本文关注的是如果图像的两个点不相邻,他们边的权值是无穷大的.这就要求必须保证新构建的无向图所有顶点都处在同一个连通的分支,否则只要有孤立点出现,就会造成算法的死循环.
2 基于梯度的优化方法
基于梯度的最短路径算法关键在于构建邻接矩阵.邻接矩阵的大小直接决定了算法时间的开销.希望找到一种方法,在保证最终骨架效果的前提下,减少前景点的数量,降低邻接矩阵的大小,从而提高算法运行效率.
由1.1中的图像的梯度可知,对图像求梯度能突出图像的边缘.针对距离变换图,能突出潜在骨架点.根据梯度的这一特性,可以对距离图求多个方向的梯度,找出所有潜在的骨架点,以达到减少搜索点的数量.这种方法特别在细节较多的情况时,更能起到好的效果.
根据实际效果和时间开销的考虑,本文只从0°、45°、90°和135° 4个方向求距离图的梯度.然后结合4个方向的梯度图,取每个梯度图对应位置灰度值最大的值作为当前像素点灰度值,形成新的梯度图.
对比图3和图2(d)容易发现,图3包括了所有潜在的骨架点和局部极大值点(连同无法用阈值消除的轮廓边界点),而且中间的脊线更加的“粗”,这样有利于最短路径算法的搜索.观察图3,容易发现,在脊线的周围有很多“毛刺”,这不利于邻接矩阵的构建.通过研究每个像素的灰度值发现,周围的“毛刺”的灰度值与中间脊线的灰度值相差较大.因此,本文利用阈值来消除大部分的“毛刺”.
本文图像的梯度是利用卷积实现的,而卷积是基于浮点操作的.因此阈值的选取也应该根据浮点的结果来选取.因为本文只是去除部分像素点,阈值越小,原图的拓扑结构保存得就越完整.通过实验的统计,阈值的取值范围为ε∈[0,8)为宜.图4是阈值为5的结果图.
虽然通过阈值的方法消除了大部分的“毛刺”点,但还有部分的离散点分布在脊线的位置.本文通过对阈值后的结果图进行取轮廓操作,脊线即为轮廓最大的那些像素点所组成的闭合集合.
虽然中间的脊线能正确的提取,但所包含的像素点还是相对较多.优化的目的是在保证拓扑结构的前提下,尽量减少最短路径搜索的像素点的数量.通过研究发现,拓扑细化的方法能够满足要求,图5为用轮廓法消除“毛刺”的结果图.简单的细化过程类似“烧草”模型[1],虽然细化的操作不能保证得到的骨架接近中轴,但本文通过梯度化的处理等操作后,细化能保证得到的初步骨架与梯度化距离图中的脊线位置重合.同时,为了保证关键点在细化过程中不丢失,本文在细化过程中,关键点被定义是端节点,不会被删除.实验证明,关键点都会落在细化的初步骨架上.
由于本文提出的优化方法在整个过程始终保持着连通性,能满足构建最短路径算法中邻接矩阵的要求.

图3 综合4方向梯度图形成的新的梯度图
Fig.3 New grads image which is conbined the grads in four directions
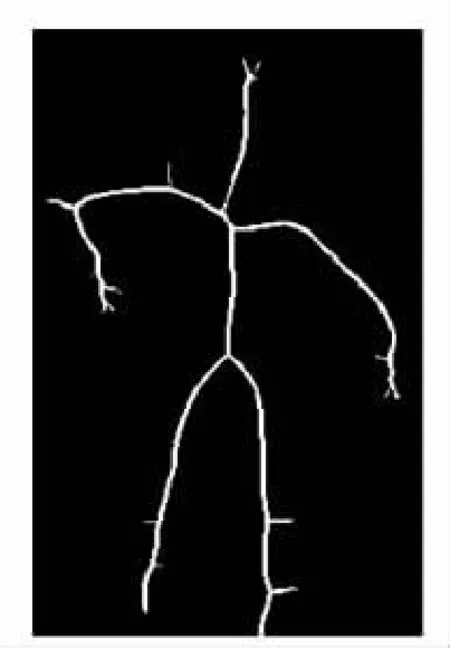
图4 阈值为5的结果图
Fig.4 Image of the result when the threshold is 5

图5 用轮廓法消除“毛刺”点的结果图
Fig.5 The result of eliminating burr by the contour method
3 算法描述
为了获得物体的曲线骨架,本文从二值图像的物体模型出发,计算其二值图的距离变换,然后梯度化距离图,寻找潜在的骨架点;之后用基于梯度的优化方法构建最短路径算法的邻接矩阵;最后用基于梯度的最短路径算法,连接所有的关键点,得到最后的骨架.算法步骤如下:
1) 计算输入二值图像I的距离变换DT,得到距离变换图SDT;
2) 求SDT中所有距离变换局部极大值点所组成的集合C={c1,c2,…},并求SDT中距离变换值最大的点s∈C;
3) 应用图3所定义的算子计算距离图SDT的梯度DT,得到梯度图S;
4) 根据集合C={c1,c2,…}和梯度图S寻找关键点集合K={k1,k2,…}⊆C;
5) 应用基于梯度的优化方法,得到点集G;
6) 根据点集G构建邻接矩阵,以s为起始点,应用基于梯度的最短路径算法,找到s到K的所有路径集合Ps→K={p1,p2,…},其中pi为s到关键点ki的最短路径;
7) 以Ps→K为基础构建一幅图像,该图像即为I的骨架图.
4 实验结果与分析
本文是在Pentium(R) Dual-Core,E6500 @2.93 G,内存2.0 G,操作系统为Window XP的PC机上,利用OpenCV2.3.1库和Visual Studio 2008实现算法.选取MPEG-7 CE Shape-1 Part B、Kimia99和Kimia216[8]中部分有代表性的二值图像,如棍形物体、多边物体、非刚性物体等,应用本文的优化算法.同时对比分析了未优化前的刘俊涛等[7]人提出基于梯度的路径算法(简称优化前算法).
4.1 误 差
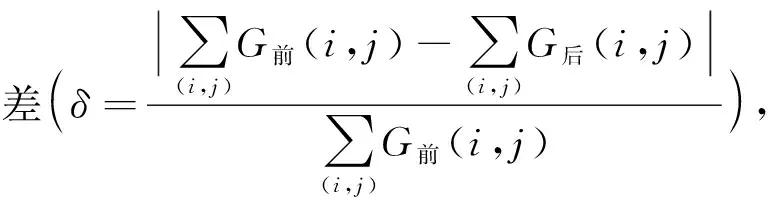
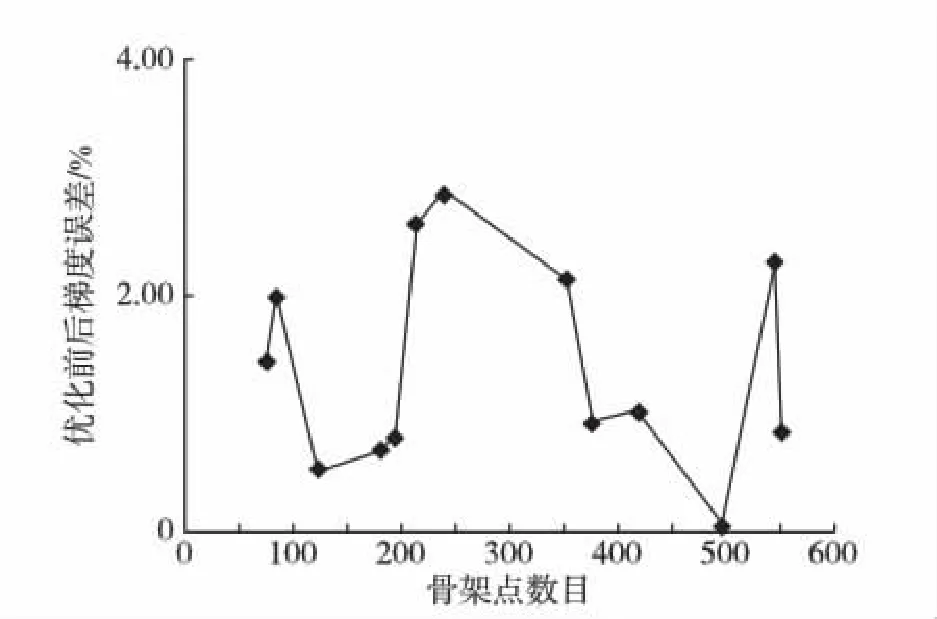
图6 优化前后梯度误差和骨架点数目关系图(ε=3)Fig.6 The connection between the number of skeleton point and gradient error before and after optimization
4.2 时 间
虽然优化前后提取的骨架效果一致,但在时间的消耗上相差很大.本文通过提取马、手掌、锤子、人体、5角图案和铅笔6种典型物体的曲线骨架,对比说明了本文优化的方法在时间开销上的优势.表1列出了6种物体运用优化前和优化后算法的时间开销.其中前4种中阈值ε=4,后2种ε=6,保证优化前后算法提取的结果是一致的.

表1 优化前和优化后时间开销对比Tab.1 Time consuming compared before and after optimization
显然,本文提出的优化方法大大地减少了基于梯度的最短路径算法的轮廓内前景点数量,减少了程序运行的时间.
4.3 阈 值
优化方法中,阈值ε的大小决定着算法时间的开销.本文在不影响提取效果的基础上,分析了4种典型刚性与非刚性、规则与不规则物体的时间开销与ε的关系.图7表明,当阈值ε达到某个临界值时,继续增大其值,将不会明显地减少程序的运行时间.
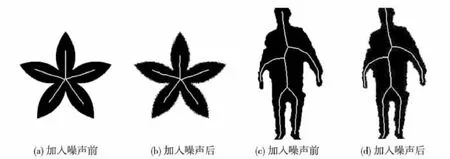
图8 加入边界噪声前后效果图对比Fig.8 The result of the image before and after joing the counter nosiy

图7 程序运行时间与阈值ε关系图Fig.7 The connection between the running time of program and the threshold
4.4 边界噪声
本文利用距离变换和图像的梯度来获取物体的骨架,由于其固有的特性,在一定程度上克服了边界噪声对骨架的影响.图8显示了不同类型物体加入噪声后,本文的优化算法提取的骨架结果图.可以发现,加入边界噪声前后的骨架图在拓扑结构上没有发现大的变化,仅在形状上有细微的差别,如线状的平滑度.
4.5 算法复杂度分析
本文假设图像大小为m×n,邻域为8邻域.下面主要从时间方面来分析本文算法的复杂度.
根据第3节所述的过程,算法时间的消耗主要表现在:1) 距离变换的计算;2) 图像梯度的计算;3) 图像轮廓的寻找;4) 细化;5) 最短路径的寻找.
距离变换是基于欧氏的变换,算法的时间复杂度控制在O(m×n).若采用基于边界跟踪的算法,虽然不能改变总体的复杂度,但大大地减少了计算的时间开销.
图像的梯度是利用图像的卷积计算得到的结果,给定一个k×k的卷积核(即本文所提到的算子),卷积计算的时间开销O((k×k)×(m×n)),其中k一般取3或5等奇数常数.因此,计算图像梯度的时间复杂度为O(m×n).
本文利用openCV提供的findContours函数来获取二值图像的轮廓.而findContours是根据suzuki85实现的,时间复杂度不会超过O(m×n).
细化是扫描图像的每一个像素,通过8邻域的关系判定每个像素是否为简单点.本文只迭代的做一次细化,因此细化的时间的复杂度为O(1×8×(m×n))=O(m×n).
搜索两个关键点之间的基于梯度的最短距离,引用Dijkstra算法,其时间复杂度为O(N2)(其中N为第3节优化后的轮廓内前景点数量).

5 结 论
本文详细介绍了基于梯度最短路径算法相关定义、原理、算法流程和复杂度分析.针对算法中邻接矩阵过大,导致算法时间开销过大的问题,提出了基于梯度的优化方法.并且采用阈值去噪和轮廓细化的方法进一步提高算法的效率,选取了MPEG-7和Kimia中部分有代表性的图片,分析对比了优化前后算法的时间开销和骨架效果.结果证明:在很好的得到单像素连通骨架的同时,本文的算法效率得到很大的提高.最后还研究了优化方法中阈值ε的大小对算法时间开销的影响.
[1] Blum H.A transformation for extracting new descriptors of shape[M].Boston:MIT Press,1967:362-380.
[2] Blum H.Biological shape and visual science(part I)[J].Journal of Theoretical Biology,1973,38(2):205-287.
[3] Bai X,Latecki L J,Liu W.Skeleton pruning by contour partitioning with discrete curve evolution[J].IEEE transactions on Pattern Analysis and Machine Intelligence,2007,29(3):449-462.
[4] Golland P,Eric W,Grimson L.Fixed topology skeletons[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Hilton Head Island,South Carolina,USA:IEEE Computer Society Press,2000:10-17.
[5] Choi W P,Lam K M,Siu W C.Extraction of the euclidean skeleton based on a connectivity criterion [J].Pattern Recognition,2003,36(3):721-729.
[6] 丁颐,刘文予,郑宇化.基于距离变换的多尺度连通骨架算法[J].红外与毫米波学报,2004,24(4):281-285.
[7] 刘俊涛,刘文予,吴彩华,等.一种提取物体线形骨架的新方法[J].计算机学报,2008,34(6):617-622.
[8] MPEG MPEG7 CE Shape-1 Part B[EB/OL].2004.http:∥www.imageprocessingplace.com/root_files_V3/image_databases.htm.
——2018年全国高考Ⅲ理科数学21题别解

