盾构法通缝隧道收敛测量的计算方法探讨

郭春生

(上海岩土工程勘察设计研究院有限公司，上海 200438)

0 引言

由于盾构法通缝隧道的自身结构、周边水土压力、行车动荷载等因素的影响，随着时间的推移，盾构隧道大多产生“横鸭蛋”形变形，为了了解这种变形量的大小，上海地区多采用全断面收敛测量的方法.全断面扫描收敛测量作为评价圆形盾构隧道断面变形情况的重要指标，与沉降、平面位移、渗漏水调查等方法一起，从不同侧面评价盾构隧道健康状况［1］.

目前，全断面扫描收敛测量数据采集一般采用全站仪、附以机载程序、沿隧道剖面按20cm左右的步长自动逐点采集，数据处理一般采用以椭圆为数据模型进行全断面整体拟合，以拟合的椭圆长轴和短轴与设计半径的较差的大小来评价变形量［2］.本文针对椭圆模型的不足，提出多弧段拟合法的数据处理改进.

1 椭圆模型拟合算法及不足

地铁隧道的拱顶下沉、两侧外扩的形变趋势，剖面呈近似的椭圆;即使隧道未发生变形，以椭圆拟合也能得到长、短相等的特殊椭圆(标准圆).因此，前些年多家测绘同行单位建立了基于椭圆模型的全断面拟合算法［3-4］.

图1基于测站仪器中心为原点、铅垂向上为Y轴、剖面内水平为X轴的数据采集坐标系内，坐标与观测量(距离D、垂直角ele)之间的关系为:

以椭圆圆心为原点、长轴为X、短轴为Y的坐标系下，各极坐标点的坐标与数据采集坐标系的转换关系:

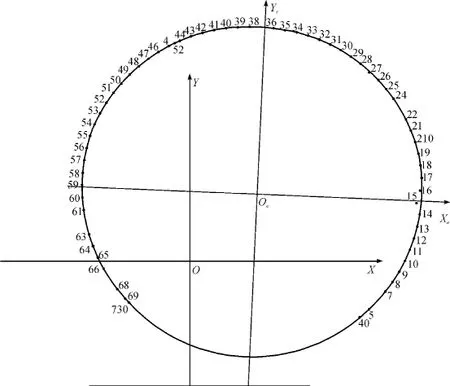
图1 椭圆模型基于圆心的坐标系

亦即(X0+RX)TΛ(X0+RX)-1=0

以所有采集点为观测值，以椭圆的参数a、b及坐标转角参数x0、y0、α为待求量，建立椭圆误差方程如下:

按最小二乘法拟合，即可求解出圆心坐标XO、长半轴、短半轴及其相对数据采集系的旋转角，进而可基于拟合的椭圆计算剖面上各位置的变形量.

长期测量数据处理实践中发现，上述处理方式存在以下不足:

(1)观测数据剔除粗差的阀值设置困难.拟合前需要剔除管线、手孔等非管片环上的粗差点，一般以实测点偏离拟合椭圆距离为阀值.粗差剔除阀值不能设得太大，其起不到自动数据处理的效果，很多点要手工删除.另一方面，由于盾构环结构特性，变形较大时，剖面内变形通常表现为相邻管片错台、相对转角，其几何特性实际已不是椭圆，较大时与椭圆偏离2 cm以上，因此粗差剔除阀值不能设得太小.断面内测距精度一般能达到2 mm以内，理想的阀值宜设置为4 mm左右，但基于椭圆模型，对于变形大的断面这个阀值将剔除很多有效观测点，显然不合适，因此观测数据自动剔除粗差的阀值设置困难.

(2)变形较大时与水平直径的直接测量值相关较大，不能提供相邻管片的错台、旋转等信息.基于椭圆模型，总体变形较小时求解的变形量与CAD中展点量测的变形量基本一致;对局部变形量较大的区段，椭圆模型把隧道剖面描述为连续的曲线，不能反映现状管片的错台、旋转情况，求解的水平直径常常与实际值相差超过10 mm，损失了较大的测量精度.

2 多弧段拟合法

大量收敛测量断面测量数据表明，由于封顶块周围土压力的分布特点，相对拱底块而言，封顶块在变形过程中容易发生竖向位移.在其变形发展过程中，各管片之间的关系(见图2).由于隧道对称，取一半隧道剖面考虑，如果封顶块向下移动，隧道管片将绕着图2所示的A点、B点、C点转动(A'、B'、C'为对称点，假定对称位移).在A点处，隧道接缝外部张开，B点处，隧道接缝内部张开，C点处，隧道接缝内部张开.由于管片钢度相对接口部位强度较大，同一管片的形态变形较小.

通过对关键成功领域进行解析与细化，明确了每个关键成功领域包含的内容、最主要因素、达成每一个成功领域的标准。如质量安全的关键绩效要素为医疗质量和医疗安全，运营管理为资产效益、成本控制和管理运营，创新发展为学科人才、新医疗新技术、教学成果、科学研究。

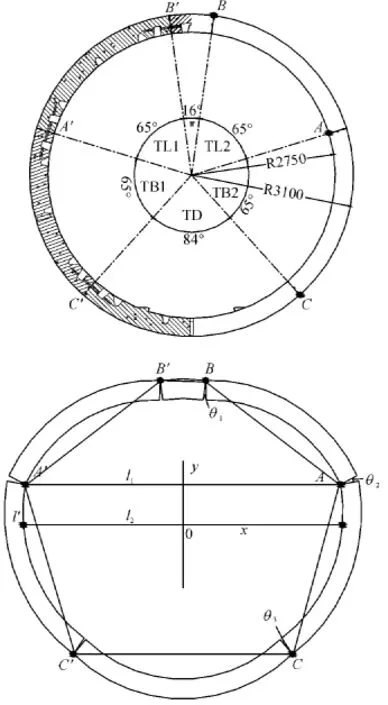
图2 通缝隧道变形特点

由于基于椭圆模型的算法存在上述不足，本文提出多弧段断面拟合的方法.本文将圆形盾构隧道看作由若干个弧段拼接而成，通过弧段各自的拟合，并把拟合后的各弧段连接成一不规则剖面，与设计断面比较，从而计算断面上各位置的变形量、横向及竖向等典型位置变形量、相邻弧段间的相对错台量与相对旋转量，实现对圆形盾构隧道的精确变形测量.观测和数据处理顺序如下.

(1)测量时，采集观测数据时应保证每个管片不少于6点，并加测相邻管片拼缝的信息(见图3).

图3 数据采集时加测拼装缝的信息

(2)把观测数据以所述管片间的拼接缝作为分界点，将圆形盾构隧道断面划分为若干弧段;按弧段模型逐一对各管片采集的数据点进行最小二乘法拟合［5-7］:

式中:(x0)T是圆心坐标，R是圆的半径对于测得点(xi)T，列出误差方程:

式中:vi相当于i点与圆周的距离.

圆心坐标的迭代初值可以取为所有测定点的坐标均值，半径初值可取为任意正数.

(3)对5个弧段逐一作为一圆形弧段模型进行拟合，计算每个采集点与拟合园心的距离Ri，并与拟合半径比较计算偏离度δi，以之为统计量、以置信度95%(大于2倍中误差)为阀值，剔除偏离度较大的粗差点后进行再次拟合.实践证明剔除粗差的阀值一般可设为4 mm，能较好地自动完成粗差点剔除;

(4)对拱底块则采用两侧最下部的观测点及拟定半径计算理论弧段，所有弧段拼接成一个全断面;

(5)在由上述5个实测数据拟合的弧段、及其拱底块按理论计算的弧段组成的剖面内，以拱底块的圆心为原点建立剖面坐标系，从而可得到:

①各观测点至原点的距离与设计半径的较差可计算隧道圆周各角度处的径向变形量;

②根据6个拼接缝观测点可确定各弧段的分界点，分界点两侧的两个弧段与分界点到原点连线平面内相交可求两个交点，两个交点的距离即为相邻块的错台量L;

③上步中两个交点处两段弧的切线之间的夹角即为相邻弧段相对旋转角a;

④计算弧段最大横向距离可求解水平向直径、计算弧段最大竖向距离可求解竖向直径.

图4 相邻管片的旋转角、错台量计算

3 算例

某圆形盾构隧道的变形量在CAD中展点后，其横径变形为0.141，其纵径变形为 -0.167，针对此圆形盾构隧道分别采用椭圆拟合算法(1)以及本文拟合方法(2)来计算其变形程度.

(1)采用传统椭圆模型解算，按每15°计算圆周上各点与圆心的距离跟理论半径比较、以向下为角度零方向、顺时针为角度正方向展开(见图5).

根据上图，采用传统的椭圆模型时:可解算出横向变形(90°处变形量+270°处的变形量)、竖向变形(180°处变形量)，且变形量与CAD展点成果相差约6 mm;但不能解算相邻管片的错台量、旋转角，使其无法全面地测量出该圆形盾构隧道的变形情况.

图5 基于椭圆模型的断面变形展开图

(2)按照本文方法，根据实测的数据，可解算出:

①5个弧段(代表上述的管片2-6)的参数(见表1).

表1 各拟合弧段参数表

②根据表1中各个弧段的拟合数据，计算相邻弧段的错台量、旋转角(见表2)，其中后管片相对前管片向外错台为正，反之为负;旋转角以外凸为正，反之为负.

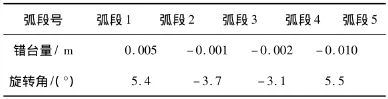
表2 相邻管片错台量、旋转角成果表

③按每15°计算圆周上各点与圆心的距离跟理论半径比较，同时纳入管缝位置点，同样以向下为 角度零方向、顺时针为角度正方向展开(见图5).

图5 基于多弧段拟合法的断面变形展开图

4 结语

实际数据处理成果表明，采用多弧段拟合法与采用传统椭圆模型解算成果图比较，更明显说明每片管片内部线性较好，变形、错台主要发生在管片与管片之间的接口部位.采用本文方法的成果与实际CAD展点图比较，除突出或凹入隧道表面的粗差点以外，各观测点偏离拟合园的距离基本不超过2 mm，并且能够通过横径变形、纵径变形、相对错台量、相对旋转角这四个方面综合评定圆形盾构隧道多弧段断面的变形程度.

［1］华锡生，黄 腾.精密工程测量技术及应用［M］.南京:河海大学出版社，2005.

［2］王解先，季凯敏.工业测量拟合［M］.北京:测绘出版社，2008.

［3］孙 昊，姚连璧，谢义林.隧道断面收敛测量与数据处理［J］.工程勘察，2010(11):44-46.

［4］黄茂华，义林谢.隧道收敛测量方法研究［J］.北京测绘，2009(4):14-16.

［5］胡龙华，王继宇，刘双成.全站仪无定向自由设站隧道收敛测量方法与精度分析［J］.华北科技学院学报，2010，7(3):40-43.

［6］宗玉玉.上海地铁隧道长期收敛测量方法研究［J］.淮海工学院学报:自然科学版，2011(S1):132-134.

［7］赵兵帅，黄 腾，欧 乐.基于椭圆拟合的隧道断面监测及其应用［J］.水利与建筑工程学报，2013(1):126-129.