基于蚁群算法的配电网谐波量测点优化配置

王艳松,孙桂龙

(中国石油大学信息与控制工程学院,山东青岛266580)

对配电网进行谐波状态估计可指导谐波治理。谐波状态估计的精度与PMU数量和位置有关，研究量测点PMU的优化配置对提高谐波状态估计的精度具有重要意义。王家林等[1-4]以潮流方程直接可解为约束；郭佩英等[5-6]以系统完全可观和冗余度最大为约束，但PMU量测冗余不一定能提高系统的精度[7]；彭春华等[8-12]研究了正常状态和N-1条件下可观测的PMU配置方法；Aminifar等[13]考虑各种突发情况(包括量测值丢失、线路中断等)规划PMU优化问题，也有学者针对PMU与SCADA系统并存且互为补充的状况[13-15]，提出了PMU优化配置方法；蒋正威等[16-18]则以提高状态估计精度为目标，研究PMU最优配置方法。上述研究主要以环式拓扑结构的输电网为研究对象，分别应用遗传算法、免疫算法和模拟退火算法、整数规划法和克隆算法等求解优化模型。笔者结合配电网的辐射状拓扑特性，确定配电网量测装置配置原则，基于配电网拓扑数学模型计算电力系统状态的可观性，提出应用蚁群算法求解配电网量测配置最优方案。

1 PMU配置的基本理论

1.1 量测配置原则

配置电能质量的量测装置一般考虑配电网节点类型和负荷类型，不要求配电网全局可观，只要满足一定可观性即可。因此，配置PMU原则如下：

(1)安装在某条母线i上的同步相量量测单元除可测量该条母线的电压外，还具备量测与该节点相关联的所有支路电流的数据通道。

(2)某条母线i装设有PMU量测，则与节点i相关联的所有节点电压相量可以通过支路欧姆定律计算得到；如果一条支路两端电压都已知，则该支路电流可通过欧姆定律计算得到。

(3)对于无配置PMU量测的零功率注入节点，该节点的所有相邻节点电压相量全部已知时，可由节点方程求出该零注入节点电压相量。该节点的相关支路电流仅一个未知，则由KCL方程可求出该未知支路电流。

(4)由于配电网的辐射状特性，若某一元素所带子代元素越多，其被选为量测点位置的概率就越大。

(5)对于支路量测来说，应将量测点设置在被量测支路的首端，以保证被量测支路处于量测装置的覆盖范围之内。

(6)配电网只对PCC节点安装量PMU量测装置。

1.2 可观测度

根据量测配置原则，配电网的可观性分为直接量测可观、直接量测间接可观和间接量测可观。直接量测可观对应着PMU安装节点(符合配置原则(1)；直接量测间接可观对应着由PMU安装节点根据配置原则(2)间接计算可观的节点；间接量测可观对应着配置原则(3)计算可观的节点。

根据配电网的拓扑结构分析量测配置的可观性。如图1所示，节点-支路关联矩阵为

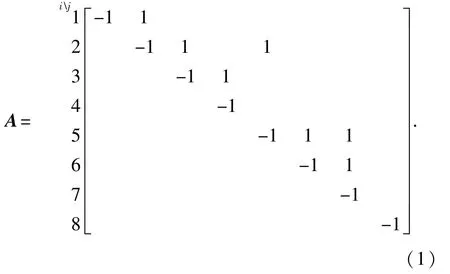
其稀疏存储格式为按行存非零非对角元素列号JU；按列存非零非对角元素行号IU；记录每行第一个非零元列号在JU中的位置IA；记录下一个非零元列号在JU中的位置LINK，对每行最后一个非零元列号的该值赋0。则在A的稀疏存储格式中，JU表示节点i的下游直连支路，IU表示点i的上游直连支路。

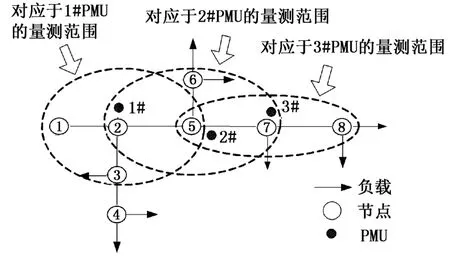
图1 安装3台PMU的配网简化图Fig.1 Installation of 3 PMUs simplified distribution network diagram

配电网中在某点i安装PMU量测覆盖范围的节点集合为Pi，集合中各节点的可观测值设为1，可用以下流程体查找在某点i安装PMU量测覆盖范围的节点集Pi：

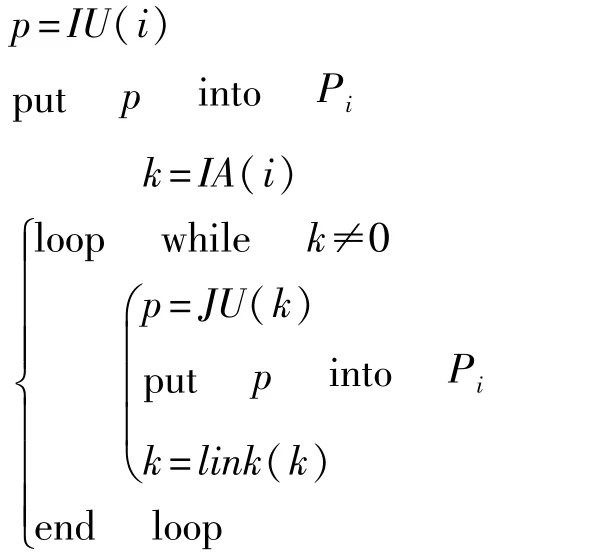
可观测度是衡量PMU系统的全局可观测性能的重要指标，定义为在当前量测配置情况下，所有可量测的节点数目相对于系统所有节点数目的比例。

1.3 冗余度

冗余度是衡量PMU量测点优化配置的重要指标，用来描述量测系统中的数据重复量测情况(含直接量测和间接量测)。冗余度定义为在当前量测配置情况下系统中各个节点被重复量测的次数之和，用∑R(i)表示。如图1所示，第2号节点被重复量测1次；第5号节点被重复量测2次；第7号节点被重复量测1次。因此，该量测系统的冗余度为4。

2、5、7号母线分别安装了PMU装置，其量测范围和系统可观测范围如表1所示。

表1 系统可观测度和冗余度Table 1 Observability and redundancy of system

2 量测点优化配置模型

在配电网配置有限个PMU可用于状态估计和谐波源定位，首先要考虑量测系统的全局可观测性水平最高，其次要考虑配置有限个PMU时，应使被重复观测的节点数目和次数最小。

量测系统的全局可观测性水平最高，可表示为可观测节点数目最多，其目标函数为

式中，n为系统的节点数；F(i)=1表示节点i可观，F(i)=0表示节点i不可观。

当存在一部分节点不可观时，应限制另一部分节点被多次重复可观。用R描述系统中各节点被重复量测的次数，如R(i)=k表示第i个节点被重复测量了k次。因此，在给定PMU配置数量的情况下，应减少量测系统的数据冗余度，即

因此，给定PMU安装数量，应减少系统可观的冗余度，增大系统可观测度，多目标最优配置数学模型为

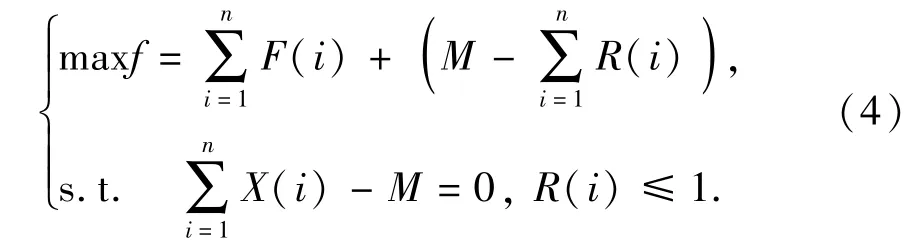
式中，n为配电网的节点数；X(i)=1表示节点i安装了PMU，X(i)=0表示节点i没有安装PMU；M为给定的PMU量测装置配置数量。

3 量测点优化配置的蚁群算法

3.1 蚁群基本原理

假设有n个城市，m只蚂蚁，城市i与城市j之间的距离用dij表示，τij表示两城市间的信息素，Jk表示第k只蚂蚁允许访问的城市，第k只蚂蚁由城市i转移到城市j的概率为

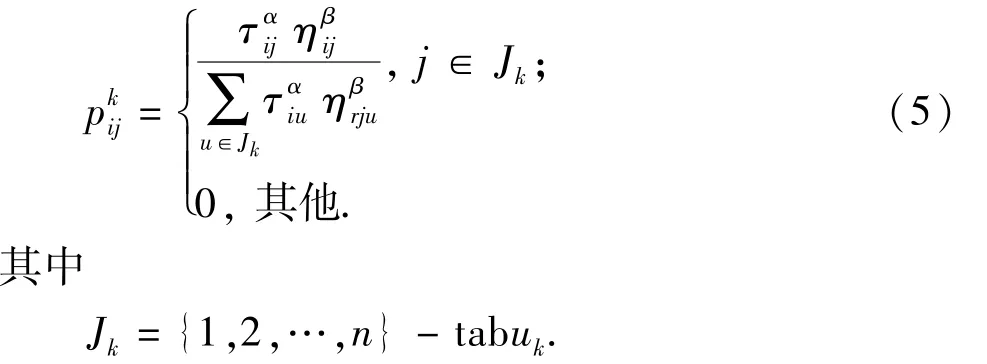
式中，tabuk用于记录蚂蚁k当前所走过的路径，此集合随着进化过程作动态调节；ηij=1/dij为线路ij的长度倒数；α、β分别表示蚂蚁在运动过程中所积累的信息素及启发式因子在蚂蚁选择路径中所起作用的大小。

随着时间的推移，各路径上以前留下的信息素逐渐消逝，用ρ参数表示信息素消逝程度，即挥发系数，蚂蚁完成一次循环，各路径上的信息素τij根据下式进行调节：

式中，Δτij为本次循环中路径ij上信息素的增加。

3.2 PMU配置的蚁群算法

将给定的PMU数目作为蚂蚁旅游的阶段数，将配电网所有节点作为蚂蚁的候选城市。根据PMU量测配置特点，状态转移和信息素更新原则如下。

3.2.1 状态移动规则

位置i的蚂蚁选择下一个节点j的公式为

式中，ηiu为节点u的可观测度F(u)；argmax{}返回的是{}取最大值时所对应的u值；q0是一个参数(0≤q0≤1)；q是(0，1)中均匀分布的随机数。每当蚂蚁要选择向哪一个节点转移时，就在[0，1]之间产生一个随机数q。根据这个随机数确定用哪种方法产生蚂蚁转移方向，然后用对应的方法产生转移。

3.2.2 信息更新规则

信息更新分为局部更新和全局更新。信息素的变化量为

式中，f为PMU优化配置的目标函数，R(j)为节点j的冗余度。每一只蚂蚁完成一次旅游，进行局部信息更新；一群蚂蚁完成一次旅游进行全局信息更新，全局更新只对每一次循环中最优解的蚂蚁所记录的路径进行全局信息更新。

在PMU安装数目一定的前提下，寻求一种能够满足系统可观测度最大、量测数据冗余度最小的优化配置蚁群算法的步骤如下：

(1)初始阶段。随机确定m只蚂蚁的初始位置，设路径上各支路的信息素都等于一常数τij=C，Δτij=0。

(2)派出蚂蚁阶段。每一只蚂蚁以一种随机策略完成一次旅游，蚂蚁从节点i选择下一节点j都依据两节点之间的转移概率pij。所有蚂蚁(m只)重复该过程。

(3)评价阶段。对每只蚂蚁完成一次旅游后进行旅游方案的评价，其评价函数即目标函数，并记录本次旅游的蚂蚁群最优旅游方案即最优解。

(4)更新信息素。按更新规则更新每条边上的信息素，每点上信息素受可观测度和冗余度两个因素影响。

(5)收敛判断。①旅行次数达到预先设定的最大次数；②所有蚂蚁都选择了同一条路径。

4 算例分析

以文献[19]所示的IEEE37节点电网为例进行分析，根据量测点配置原则，只以PCC节点作为寻优范围来研究PMU的优化配置方案。

将IEEE37系统中的非公共节点的末端负荷节点进行简化，网络简化后重新进行节点优化编号，如图2所示。根据配电网节点数，按经验PMU配置数目通常为网络节点数目的1/3～1/5，根据配电网节点类型和负荷的性质，不需要完全可观。因此，该算例给定5台PMU，优化算法所求得的最优配置方案结果并非唯一的，但对配电网可观测度均达到90.9%，如表2所示。五种配置方案都在14和18号节点处配置了PMU，说明14和18号节点为枢纽量测点；不同的配置方案虽然实现了相同的最大可观测度，但其量测范围不尽相同，这为电网规划提供了多种选择，可以结合配电网负荷性质和电网的实际框架特点选择一种符合实际的规划方案。

图2 IEEE37节点电网的简化拓扑图Fig.2 Simplified network diagram for IEEE 37-node system

表2 5台PMU的多种可供选择的配置方案Table 2 Several alternative optimal allocation results of 5 PMUs

5 结 论

(1)根据配电网的节点-支路关联矩阵数学模型的稀疏存储技术，可以分析谐波量测点覆盖的节点可观测性。

(2)以节点可观测度和冗余度为目标建立数学模型，减少节点不必要的可观冗余度，增大可观节点数目。

(3)配电网节点多分支多，各节点用户性质不同，不要求全局可观，给定PMU配置经验数目，应用蚁群算法的个体寻优和群体寻优交互进行的优点能得到多个合理的规划方案。算例分析验证了算法的有效性。

[1] 王家林，夏立，吴正国，等.采用量子遗传算法的电力系统PMU最优配置[J].高电压技术，2010，36(11)：2838-2842.WANG Jia-lin，XIA li，WU Zheng-guo，et al.Optimal PMU placement of the power system using quantum genetic algorithm[J].High Voltage Engineering，2010，36(11)：2838-2842.

[2] 李新振，滕欢.考虑潮流方程直接可解的PMU最优配置[J].电力系统保护与控制，2009，37(16)：63-67.LI Xin-zhen，TENG Huan.Optimal configuration of PMU considering direct solvable power flow[J].Power System Protection and Control，2009，37(16)：63-67.

[3] 王家林，夏立，吴正国，等.船舶电力系统相量测量单元多目标优化配置问题[J].高电压技术，2012，38(5)：1267-1273.WANG Jia-lin，XIA li，WU Zheng-guo，et al.Optimal phasor measurement units placement considering multiobjectives in shipboard power system[J].High Voltage Engineering，2012，38(5)：1267-1273.

[4] 王家林，夏立，吴正国，等.电力系统PMU最优配置新方法[J].电力系统及其自动化学报，2011，23(6)：1-5.WANG Jia-lin，XIA li，WU Zheng-guo，et al.New method of optimal PMU placement of the power systems[J].Proceedings of the Chinese Society of Universities for Electric Power System and its Automation，2011，23(6)：1-5.

[5] 郭佩英，郝红艳，邓颖，等.考虑测量冗余度最大的电力系统PMU最优配置[J].东北电力大学学报，2010，30(2)：31-35.GUO Pei-ying，HAO Hong-yan，DENG Ying，et al.Optimal configuration of PMU in power system considering the biggest measurement redundancy[J].Journal of Northeast Dianli University，2010，30(2)：31-35.

[6] CHAKRABARTI S，KYRIAKIDES E.Optimal placement of phasor measurement units for power system observability[J].IEEE Transactions on Power System，2008，23(3)：1433-1440.

[7] 王艳松，韩美玉，谭志勇.基于遗传算法的PMU配置对谐波状态估计质量影响的研究[J].电力系统保护与控制，2010，38(21)：33-36.WANG Yan-song，HAN Mei-yu，TAN Zhi-yong.Study on the effect of PMU allocation on the quality of harmonic state estimations[J].Power System Protection and Control，2010，38(21)：33-36.

[8] 唐岚，吴军基.基于电网脆弱性和经济性评估的PMU最优配置新方法[J].电网技术，2012，36(8)：260-264.TANG Lan，WU Jun-ji.A new method for optimal PMU configuration considering vulnerability of power system and economy[J].Power System Techonology，2012，36(8)：260-264.

[9] 彭春华.用免疫BPSO算法和N-1原则多目标优化配置 PMU[J].高电压技术，2008，34(9)：1971-1976.PENG Chun-hua.Multi-objective optimization for PMU placement based on immune BPSO algorithm and N-1 reliability test principle[J].High Voltage Engineering，2008，34(9)：1971-1976.

[10] 陈刚，唐毅.基于田口法考虑N-1情况的PMU优化配置方法[J].电力系统自动化，2010，34(13)：28-32.CHEN Gang，TANG Yi.Optimal PMU placement based on Taguchi method considering N-1 condition[J].Automation of Electric Power Systems，2010，34(13)：28-32.

[11] 刘新东，江全元，曹一家.N-1条件下不失去可观测性的PMU优化配置方法[J].中国电机工程学报，2009，29(10)：47-51.LIU Xin-dong，JIANG Quan-yuan，CAO Yi-jia.Optimal PMU placement to guarantee observability under N-1 condition[J].Proceedings of the CSE，2009，29(10)：47-51.

[12] 蒋正威，曹一家，孙维真.基于01整数规划的多目标最优PMU配置算法[J].电力系统保护与控制，2008，36(21)：12-17.JIANG Zheng-wei，CAO Yi-jia，SUN Wei-zhen.Multiobject PMU optimization placement algorithm based on 01 integer program[J].Power System Protection and Control，2008，36(21)：12-17.

[13] AMINIFAR F，KHODAEI A，FOTUHI-FIRUZABAD M，et al.Contingency constrained PMU placement in power networks[J].IEEE Transactions on Power System，2010，25(1)：516-523.

[14] 李虹，李卫国.基于提高系统可观测性和状态估计精度的PMU配置[J].华北电力大学学报，2011，38(1)：31-34.LI Hong，LI Wei-guo.A new method of PMU placement for improving network observability and state estimation precision[J].Journal of North China Electric Power U-niversity，2011，38(1)：31-34.

[15] 乔立慧，孔红，薛辉，等.考虑SCADA量测的PMU优化配置研究[J].华北电力技术，2010(4)：5-9.QIAO Li-hui，KONG Hong，XUE Hui，et al.Study on optimal configuration of PMU with SCADA measurements[J].North China Electric Power，2010(4)：5-9.

[16] 蒋正威，李继红，孙维真.基于不可观测深度的分阶段PMU配置算法[J].电网技术，2008，32(16)：81-85，90.JIANG Zheng-wei，LI Ji-hong，SUN Wei-zhen.Staged PMU placement algorithm based on depth of unobservability[J].Power System Technology，2008，32(16)：81-85，90.

[17] 李虹，李卫国，彭书涛，等.WAMS中的PMU最优配置新方法[J].高电压技术，2009，35(2)：415-419.LI Hong，LI Wei-guo，PENG Shu-tao，et al.New method of optimal PMU placement in WAMS[J].High Voltage Engineering，2009，35(2)：415-419.

[18] ABBASY N H，ISMAIL H M.A unified approach for the optimal PMU location for power system state estimation[J].IEEE Transactions Power Delivery，2009，24(2)：806-813.