不同流变模式钻井流体圆管层流压耗的通用精确算法

樊洪海,彭 齐,腾学清,周号博,李朝玮,汤化沙

(1.中国石油大学石油工程学院,北京102249；2.中国石油塔里木油田分公司,新疆库尔勒841000)

非牛顿流体管流压耗计算是钻井水力学的基础，涉及到钻井、压井、注水泥顶替等相关工艺过程。随着油气钻探向深层和深水的发展，钻遇的复杂地层越来越多，钻井液及水泥浆体系也越来越复杂，常用的流变模式(宾汉、幂律、卡森等)[1-3]已不能满足钻井工程需要。近些年一些更为复杂的流变模式被用于描述钻井液和水泥浆的流变性，如三参数(赫-巴、罗-斯，Sisko等模式)模式[4-7]和四参数模式[8]等，这些模式的引入提高了钻井液与水泥浆实际流变性描述的精度，但依据传统研究方法将这些流变模式用于水力计算仍然存在一定的难度。笔者利用通用圆管流量方程[9]，提出一种适用于不同流变模式钻井流体圆管层流压耗的通用精确算法，并给出部分流变模式圆管层流计算压耗的具体方程。

1 求解圆管层流压耗的传统方法

钻井液和水泥浆大都属于非牛顿流体，研究非牛顿流体圆管层流传统方法的基本步骤如下。

(1)假设流体在圆管内流动满足：黏性层流(或结构流)；稳定流动；均匀流；沿管壁无滑动。在上述假设条件下，根据压耗Δp与剪切应力τ的平衡关系建立圆管均匀流控制方程，表达式为

式中，τ为速梯区任意半径r处的切应力；Δp为L流程长度的压耗；L为圆管长度。在管壁r=R处有

式中，τw为管壁切应力；R为圆管半径。

(2)将给定的流变方程与圆管均匀流控制方程(1)联立，获得该非牛顿流体圆管层流的速度微分方程，考虑边界条件并积分得到圆管层流的速度分布方程u=u(Δp)。

(3)在圆管断面上对速度分布方程u=u(Δp)进行面积积分，对于某些流变模式情况略去部分高次项后得到流量表达式Q=Q(Δp)，进而求得平均流速方程v=v(Δp)。

(4)求平均流速方程v=v(Δp)的反函数得到压耗计算模型Δp=v-1(v)。

表1列出了使用传统分析方法获得的常用流变模式的圆管层流压耗计算公式。为了得到显式的压耗计算公式，求解过程中对于大部分流变模式需进行简化处理，导致计算结果存在误差。在某些特殊情况下误差可能会很大。因此，有必要研究更精确的压耗计算方法。

表1 传统方法压耗计算模型Table 1 Pressure drop equations of conventional methods

2 圆管层流压耗的通用精确算法

2.1 通用圆管流量方程

管流的流量表达式为

对式(3)进行分部积分，可写成

在管壁处有，因此。由流变方程知，剪切速率可表示为，于是式(4)化简为

由式(1)和式(2)可得

将式(6)代入式(5)，得

式(7)为Herzog和Weiseenberg[10]给出的描述流量和管壁切应力关系的一般性方程，称为通用圆管流量方程[9-12]。从推导过程可以看出，通用圆管流量方程与流变模式无关，可适用于任意与时间无关的非牛顿流体。

对于带屈服值的黏塑性流体圆管结构流(存在流核)，式(7)可写为

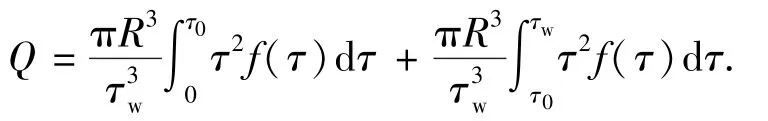
因流核内剪切速率f(τ)=γ=0，有，则黏塑性流体结构流圆管流量方程为

2.2 通用精确算法压耗模型的建立

由通用圆管流量方程式(7)和式(8)可以看出，若流体的类型已知，即给定流体的流变方程f(τ)的具体形式，通过积分就可导出该流变模式流体圆管层流(或结构流)时流量Q与管壁切应力τw的具体关系式。已知流量Q，可解出管壁切应力τw，进而通过式(2)求得压耗Δp。这就是通用精确算法计算压耗的基本思路。下面分别以罗-斯和Sisko模式为例详述分析过程。

(1)罗-斯模式。因罗-斯模式流体具有屈服值，故将其流变方程τ=A(γ+C)B代入式(8)，得

积分并整理，得

若流量Q已知，可通过数值方法(二分法、牛顿迭代法等)求解式(9)得到管壁切应力τw，再由式(2)的第二式计算压耗Δp。

(2)Sisko模式。Sisko模式流体没有屈服值，将Sisko模式的流变方程τ=aγ+bγn和 dτ=(a+bnγn-1)dγ代入式(7)，得

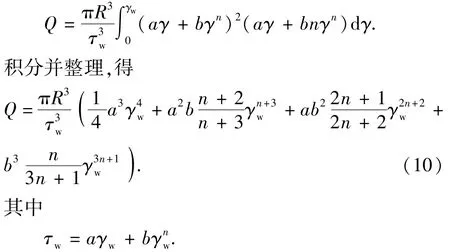
式(10)中管壁剪切速率γw同样可以通过数值方法迭代求解得到，然后通过Sisko流变方程即可得到管壁处切应力τw，最后由式(2)的第二式计算压耗 Δp。

常用流变模式的流量精确关系式见表2。

表2 圆管流量公式对比Table 2 Contrast of flow formulas in pipe

传统算法相对于通用精确算法存在的误差主要来源于其在推导流量关系式过程中略去的某些高阶项，如宾汉模式省略了，卡森模式和罗伯逊斯蒂夫模式省略了以及更高次项等。

对于流变方程比较复杂的Sisko模式及四参数模式，由于流变方程的反函数无法表示，因此无法通过积分得到流量计算表达式；而通用精确算法则可直接通过通用圆管流量方程得到管壁切应力τw与流量Q的关系式，进而求解压耗，具有普适性。

3 传统方法的误差分析

为了分析传统方法压耗计算结果的误差，将传统方法与精确算法的流量分别记为Qc和Qa，以表示流量计算结果的误差，分析其随流体屈服值与管壁切应力之比τ0/τw的变化情况。宾汉模式和卡森模式的分析结果见图1，赫-巴模式的分析结果见图2。

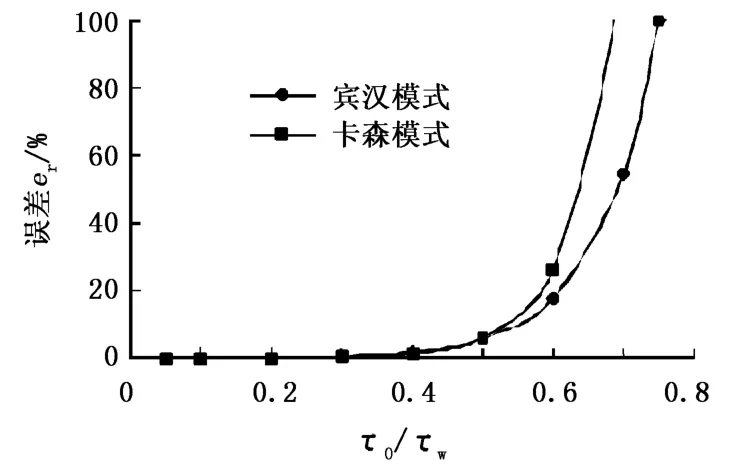
图1 二参数模式误差分析Fig.1 Error analysis of two parameters model

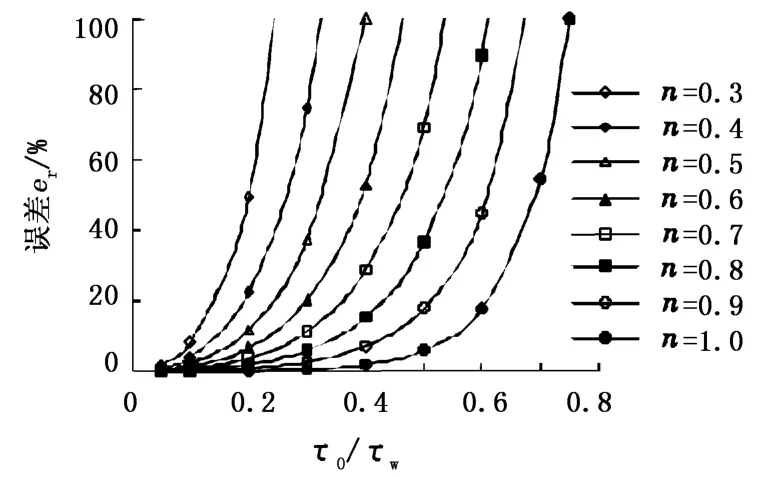
图2 赫-巴模式误差分析Fig.2 Error analysis of H-B model

由图1可以看出，τ0/τw＜0.5时(对应于低屈服值流体或较高流速情况)，误差很小；τ0/τw＞0.5时(对应于高屈服值流体或较低流速情况)，误差较大，而且随τ0/τw的增加，误差逐渐增大。另外，由卡森模式和宾汉模式对比看出，不同流变模式误差变化的趋势有一定差异。

分析赫-巴模式时发现关系式与流性指数n(0＜n≤1)有关，图2中列举了部分n值下的赫-巴模式误差变化曲线。图2中揭示的规律与图1一致，即传统算法相对于精确算法的计算误差随着流体屈服值的增大而增大，只不过这种增大的程度随着赫-巴模式流性指数n的增大而变得迟缓。

4 试验验证

通过两组来源于怀俄明大学[13]试验数据对两种压耗计算方法做进一步的说明。试验采用的钻井液由水、黏土、重晶石及聚合物组成，具有较高的屈服应力值及较强的剪切稀释性，其密度为1 036.5 kg/m3。圆管长10.973 m，图3为卡森模式5.08 cm圆管计算结果，图4为赫-巴、罗-斯、四参数3种模式2.54 cm圆管计算结果，详细数据参考文献[13]。

图3 卡森模式压耗对比Fig.3 Pressure drop contrast of Casson model

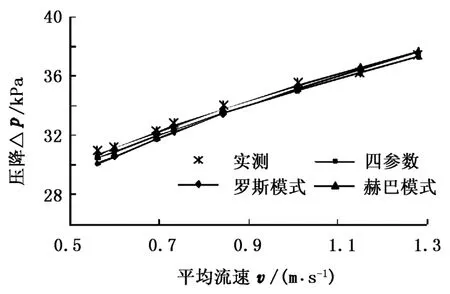
图4 精确算法压耗分析Fig.4 Pressure drop analysis of accurate method

由图3可知，精确算法得到的压耗不论是在低排量还是在高排量条件下都能够较好地与实测结果相吻合。传统方法在圆管排量很低(管内平均流速小于0.6 m/s)的情况下得不到圆管压耗，在中低排量(管内平均流速为0.6～0.9 m/s)条件下与实测结果相差较大，但随着排量增大传统算法的误差不断减小，且趋近于实测结果。

图4表明采用3种不同模式精确算法计算结果都非常逼近实测结果，其中以赫-巴模式与实测结果吻合最好，罗-斯模式和四参数模式吻合程度稍差一些。从理论上讲，精确算法得到的是圆管层流压耗的精确解。不同模式计算结果存在差异，主要是因为试验用钻井液的实际流变性与不同流变模式的吻合程度有差异，该组试验用钻井液的流变性更符合赫-巴模式，故赫-巴模式的压耗计算结果与实测数据吻合最好。

5 结 论

(1)在已知非牛顿流体流变方程的条件下，可以利用通用圆管流量方程建立流量与管壁切应力或管壁剪切速率的精确关系式，通过该关系式由给定的流量求解管壁切应力，进而获得圆管层流压耗精确值。这种方法适用于所有流变模式钻井流体圆管层流，具有普适性好、建模过程简单、模型精度高等特点。

(2)圆管层流压耗传统算法的误差主要取决于流体屈服值与管壁切应力比值，或者说取决于流体屈服值和平均流速。流速一定时，流体屈服值越大则计算误差越大；流体的屈服值一定时，流速越大，计算误差越小。另外，赫-巴模式、罗-斯模式等的计算误差还与其流性指数相关。

(3)对于一些相对复杂的流变模式，传统方法无法建立压耗计算模型，而利用本文的精确算法可以很容易地建立起这些流变模式的压耗计算模型。该方法为一些复杂的流变模式在钻井工程及其他工程领域的推广应用提供了良好的基础。

[1] 陈家琅.钻井泥浆的管流公式集[J].大庆石油学院学报，1981，4(3)：99-111.CHEN Jia-lang.The formulary for pipe flow of drilling mud[J].Journal of Daqing Petroleum Institute，1981，4(3)：99-111.

[2] 西南石油学院泥浆流变学研究组.适合于钻井液的流变模式的初步评价[J].西南石油学院学报，1983，5(4)：17-37.Mud-Rheology Research Group.Evaluation of the rheologic models of drilling fluids[J].Journal of Southwest Petroleum Institute，1983，5(4)：17-37.

[3] WANG Zhong-ying，TANG Song-ran.Casson rheological model in drilling fluid mechanics[R].SPE 10564，1982.

[4] 刘崇建.带屈服值的幂律流变模式在钻井泥浆中的应用[J].天然气工业，1982，2(3)：46-55.LIU Chong-jian.Application of yield power-law model in drilling muds[J].Natural Gas Industry，1982，2(3)：46-55.

[5] HERSCHEL W H，BULKLEY R.Measurement of consistency as applied to rubber-benzine solutions：Proc 29thAnnulal Meeting of the American Society of Testing Materials，Atlantic City，1926[C].Atlantic，1926：621-633.

[6] ROBERTSION R E，Jr STIFF H A.An improve mathematical model for relating shear stress to shear rate in drilling fluids and cement slurries[R].SPE 5333，1976.

[7] SISKO A W.The flow of lubricating greases[J].Industrial&Engineering Chemistry，1985，50(12)：1789-1792.

[8] 樊洪海，王果，张辉，等.四参数流变模式及其水力计算模型[J].石油学报，2010，31(3)：511-515.FAN Hong-hai，WANG Guo，ZHANG Hui，et al.A four-parameter rheological model and its hydraulic calculation formulas[J].Acta Petrolei Sinica，2010，31(3)：511-515.

[9] GOVIER G W，AZIZ K.The flow complex mixtures in pipes[M].New York：Van Nostrand Reinhold，1972：183-185.

[10] HERZOG R O，WEISSENBERG K.Ueber die thermische，mechanische und röntgenoptische analyse der quelling[J].Kolloid-Zeitschrift，1928，46：277-289.

[11] RABINOWITSCH B.Verber die viskositat und elastizital von solen[J].Phisik Chemistry，1929，145：1-26.

[12] MOONEY M.Explicit formulas for slip and fluidity[J].Journal of Rheology，1931，2(2)：210-222.

[13] OKAFOR M N.Experimental verification of the roberston-stiff model for drilling fluids[D].Laramie：University of Wyoming，1982.