利用径向成层介质的Green函数和积分方程模拟含金属套管井间电磁场的响应

魏宝君,陈 涛,侯学理,冯琳伟,党 峰,陈章龙

(1.中国石油大学理学院,山东青岛266580；2.中国石油集团测井有限公司,陕西西安710077)

井间电磁探测技术由于具有更大的横向探测范围而成为油气藏研究的重要手段之一，数值模拟方法和成像方法是该技术的重要组成部分。传统的井间电磁数值模拟方法和成像方法研究均基于无金属套管的井眼环境[1-6]，而在很多情况下井间电磁测量可能在发射井或接收井中有金属套管的井眼环境下进行[7]，其测量数据与无金属套管环境下的测量数据存在较大差别，因而有必要研究金属套管对井间电磁场的影响。笔者将求解积分方程的BCGS算法[8-9]与径向成层介质Green函数的递推矩阵方法[10]相结合，将金属套管作为一层特殊介质包含到Green函数中，计算区域为井间地层，模拟发射井含金属套管时轴对称二维井间电磁场的响应，分析金属套管对井间电磁场的影响规律。

1 积分方程

所采用的轴对称二维井间地层模型见图1，该模型包含了井眼、发射井金属套管、井间均质背景地层和电导率异常区域。采用圆柱坐标系，忽略位移电流的影响并假设地层是非磁性的，其磁导率取真空中的数值μ0，均质背景地层的电导率设为σb。将发射线圈视为磁偶极子并假设发射源随时间的变化关系为exp(iωt)，其中ω为角频率，则接收井中接收线圈处磁感应强度的轴向分量可表示为如下积分方程的形式[5]：

式中，rT、rR分别为发射线圈和接收线圈的位置坐标，D为电导率异常区域；(rR，r′)为径向成层地层r′处的单位圆电流元在接收点rR处的Green函数；Δσ(r′)为异常区域与背景地层电导率之差，Δσ(r′)=σ(r′)-σb(r′)；A(r′，rT)为发射线圈在电导率异常区域内产生的总磁矢势(只有φ分量)；Bb(rR，rT)=μ0NTIT(rR，rT)为发射线圈在径向成层地层中产生的磁感应强度的轴向分量，NT为发射线圈匝数，IT为发射线圈电流强度。式(1)称为数据方程，若电导率异常区域内的总磁矢势A(r′，rT)已知，由该式可获得接收线圈处磁感应强度的轴向分量。

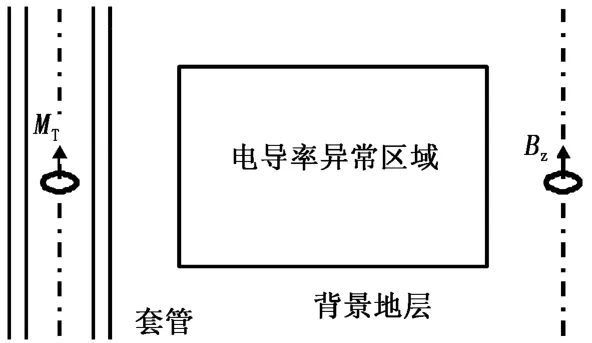
图1 含套管轴对称二维井间地层模型简图Fig.1 Schematic configuration of axial symmetric 2-D cross-hole formation model with metal casing

在异常区域D内，总磁矢势A(r，rT)满足如下积分方程[5]：

式中，Ab为磁矢势的背景值；Γ(r，r′)为径向成层地层磁矢势Green函数。

将电导率异常区域D分成N个小单元Dj，每个小单元内地层电导率恒定，设为σj，并假设在每个小单元内磁矢势恒定，并由其中心点的值代替，则式(1)可离散为

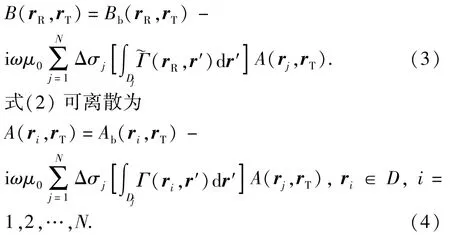
式(4)可表示为如下线性形式：

其中I为线性算子，定义为

式(6)可采用稳定型双共轭梯度(BCGS)方法进行迭代求解[8-9]，从而得到总磁矢势在区域D内的分布。求解式(6)时先对所有小单元给定任意初始猜测值A0(例如A0=0)，并计算下列残差：

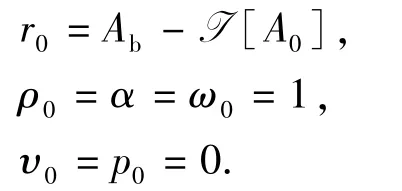
选择任一量0满足(0，r0)≠0，比如0=r0，第k步的迭代顺序为

当小于给定的误差标准时，迭代终止。

2 径向成层地层的Green函数及其对空间坐标的积分

2.1 径向成层地层的Green函数

在上述积分方程表达式中，含有对径向成层地层 Green 函数(rR，rT)、Γ(r，rT) 及积分的计算，可采用文献[10] 的递推矩阵方法。设径向成层地层共有n+1层，由里向外的编号为l=0，1，…，n，各层半径为r0，r1，…，rn-1，单位圆电流发射源在第j层，各层电参数分别为μl、εl。任意第l层内的 Green函数Γl(r，r′) 可表示为如下形式：

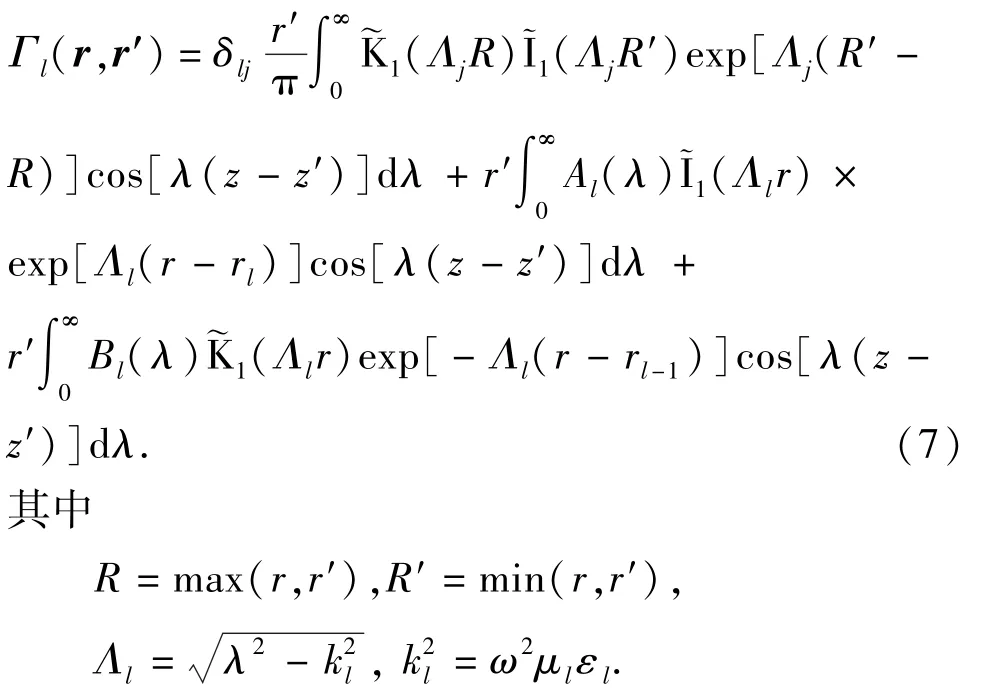
式中，ν和ν分别为扣除指数项后的第一类和第二类ν阶复宗量变型Bessel函数。将变型Bessel函数的指数项单独列出计算可避免上溢现象[10]。其中，Al(λ)和Bl(λ)为待定系数，由圆柱形层界面处电场和磁场的连续性条件确定，可采用递推矩阵方法快速求解[5，10]。

由式(7)利用变型Bessel函数对径向坐标的微分关系可得到l(r，r′)，若r＞r′，有

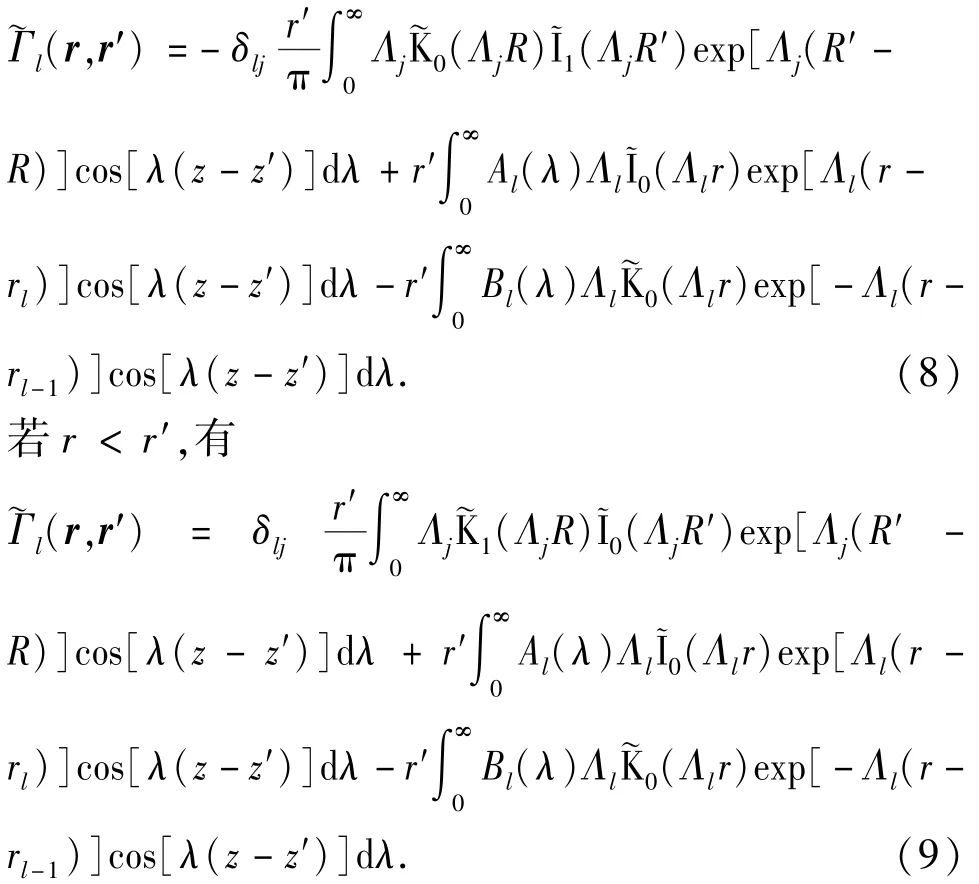
利用式(8)可计算井间无电导率异常体时接收线圈处磁感应强度的轴向分量Bb(rR，rT)。

2.2 Green函数对空间坐标的积分

设某一矩形小单元De中心点的坐标为(rc，zc)、其径向和轴向宽度分别为Δr、Δz，在该单元内对Green 函数Γl(r，r′) 积分，有

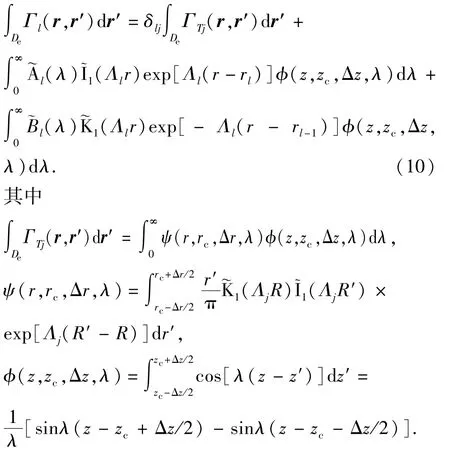
待定系数由下列方程得到：

其中，，矩阵M的表达式见文献[10]。结合文献[10]经推导可得到的各非零元素为

在该单元内对 Green 函数l(r，r′) 积分，有

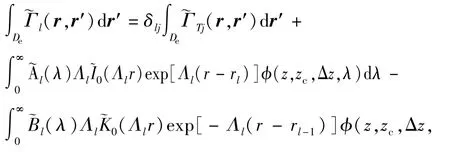
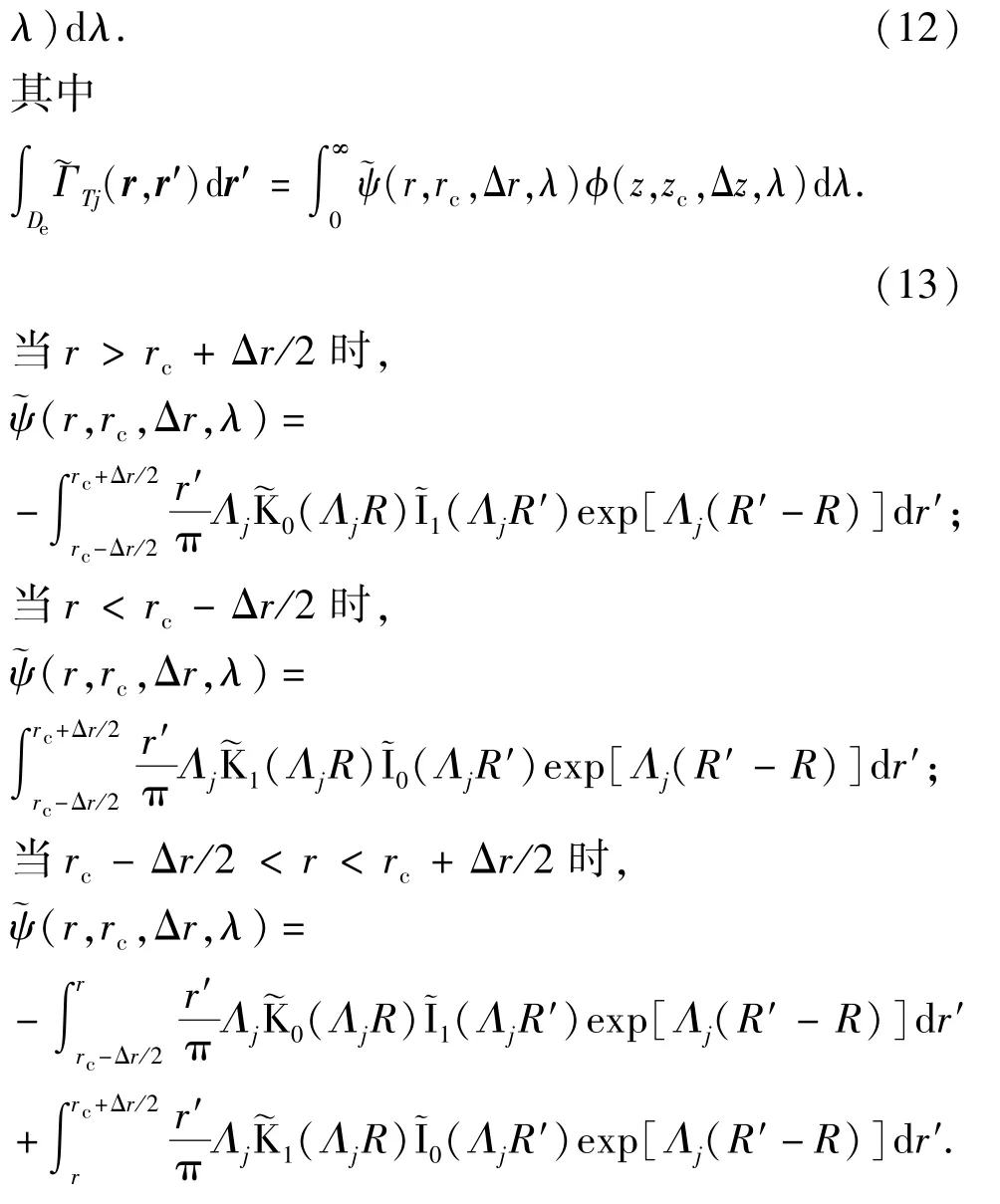
求解式(11)亦采用递推矩阵方法。

3 数值模拟举例

3.1 有电导率异常区块时的井间电磁场

设发射源磁偶极矩MT=1 Am2、井间距为100 m、金属套管的内外半径分别为8 cm和10 cm、金属套管的电导率为5×105S/m、发射井内钻井液电导率为0.05 S/m、发射频率为100 Hz。模型1为井间存在一个电导率异常区块的情况。固定发射源垂向坐标为15 m，电导率异常区块的范围为径向30～70 m、垂向10～50 m，小单元数目为20×20=400，每个小单元的尺寸为2 m×2 m。图2给出了井间背景地层电导率为0.2 S/m、异常区块电导率为2.0 S/m时有金属套管和无金属套管情况下的磁感应强度随接收线圈垂向坐标zR的变化关系。图3给出了井间背景地层电导率为1.0 S/m、异常区块电导率为0.02 S/m时有金属套管和无金属套管情况下的磁感应强度随接收线圈垂向坐标的变化关系。

图2 模型1第一种情况下有金属套管和无金属套管时总磁感应强度随接收线圈垂向坐标的变化关系Fig.2 Relationship between total magnetic induction intensity with or without metal casing and receiver coil's vertical position for the first case of model 1

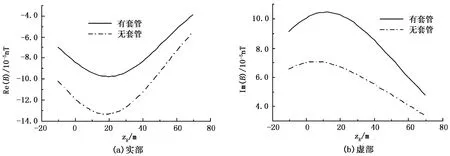
图3 模型1第二种情况下有金属套管和无金属套管时总磁感应强度随接收线圈垂向坐标的变化关系Fig.3 Relationship between total magnetic induction intensity with or without metal casing and receiver coil's vertical position for the second case of model 1

由上述算例可以看出，有金属套管时实部磁感应强度的数值要小于无金属套管时的磁感应强度值，而有金属套管时虚部磁感应强度的数值要大于无金属套管时的磁感应强度值。计算发现，对磁感应强度的总幅度值而言，由于金属套管对电磁信号的吸收，有金属套管时磁感应强度的总幅度值要小于无金属套管时的磁感应强度的总幅度值。另由图2和图3发现，当有金属套管存在时除实、虚部磁感应强度的数值发生变化外，其响应曲线沿垂向坐标出现“平移”，即两种情况下磁感应强度的极值点不再对应接收线圈的同一垂向坐标，且虚分量的“平移”现象更加明显。这说明金属套管的存在还导致了磁感应强度相位的改变。

模型2为井间存在两个电导率异常区块的情况，取井间背景地层电导率值为1.0 S/m，固定发射源垂向坐标为40 m。第一个电导率异常区块的范围为径向30～70 m、垂向10～30 m，电导率为5.0 S/m。第二个电导率异常区块的范围为径向30～70 m、垂向50～70 m，电导率为0.02 S/m。每个小单元的尺寸仍为2 m×2 m。图4给出了该模型有金属套管和无金属套管时的磁感应强度随接收线圈垂向坐标的变化关系。由该算例可得到类似结论。

图4 模型2有金属套管和无金属套管时总磁感应强度随接收线圈垂向坐标的变化关系Fig.4 Relationship between total magnetic induction intensity with or without metal casing and receiver coil's vertical position for model 2

3.2 井间地层电导率改变时金属套管的影响

假设井间无电导率异常块，并假设发射线圈和接收线圈具有相同的垂向坐标，其余参数同上。图5和图6给出了有金属套管和无金属套管两种情况下频率分别为50 Hz和500 Hz时接收线圈处的磁感应强度随井间均质地层电导率的变化关系。由图5和图6可以看出，在频率为50 Hz情况下，金属套管的影响较小，当频率为500 Hz时，金属套管的影响明显增大。就磁感应强度的幅度而言，由于金属套管的存在导致穿过套管的电磁信号变弱，故有金属套管情况下磁感应强度的幅度变小。但金属套管对磁感应强度幅度值的影响是近似恒定的，即对于不同的地层电导率，有金属套管和无金属套管情况下磁感应强度幅度的比值近似恒定。这个比值取决于金属套管的参数和频率，与地层电导率无关。就磁感应强度的实分量和虚分量而言，变化关系要复杂，主要是存在曲线的“平移”且虚分量更加明显，这同样说明金属套管亦引起磁感应强度相位的变化。

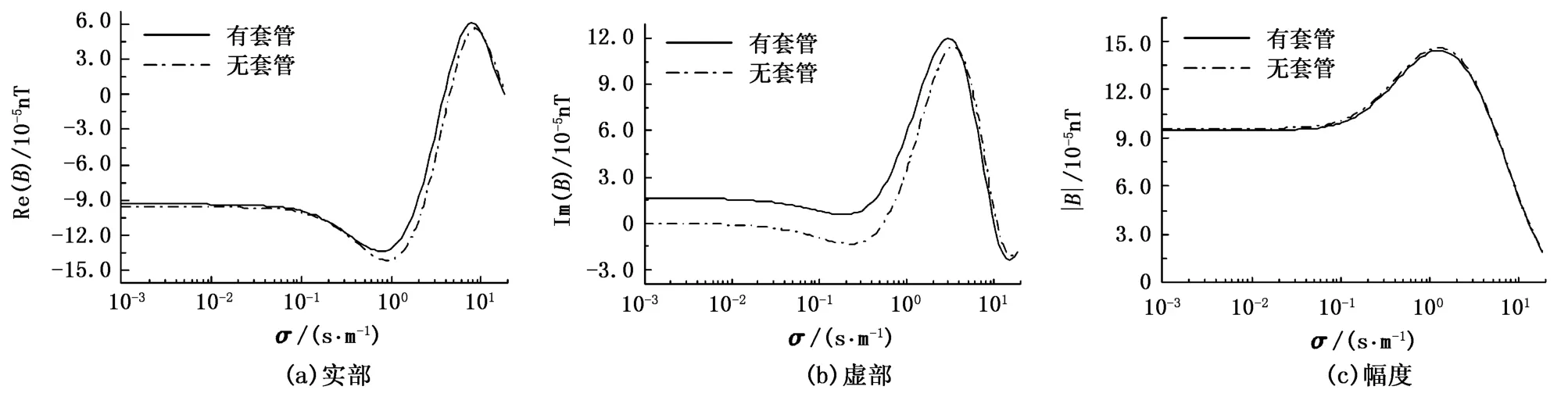
图5 频率为50 Hz时磁感应强度随井间均质地层电导率的变化关系Fig.5 Relationship between magnetic induction intensity and homogeneous cross-hole formation's conductivity for the frequency of 50 Hz

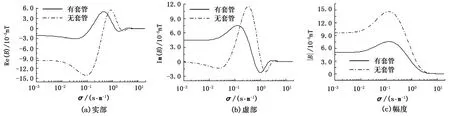
图6 频率为500 Hz时磁感应强度随井间均质地层电导率的变化关系Fig.6 Relationship between magnetic induction intensity and homogeneous cross-hole formation's conductivity for the frequency of 500 Hz

3.3 金属套管电导率对井间电磁信号的影响

假设井间均质地层电导率为0.1 S/m，其余参数不变，图7给出了频率分别为50 Hz和500 Hz时接收线圈处的磁感应强度随金属套管电导率σc的变化关系。由图7可以看出，在套管电导率很小时，其影响可以忽略不计。当套管电导率增大到某一临界值时导致磁感应强度快速变化。当套管电导率增加到该临界值时，磁感应强度的实分量值快速减小，此后逐渐稳定到一个较低数值；而磁感应强度的虚分量先增加再快速减小，此后逐渐稳定到一个数值。套管电导率的临界值与频率有关，频率越高临界值越小。

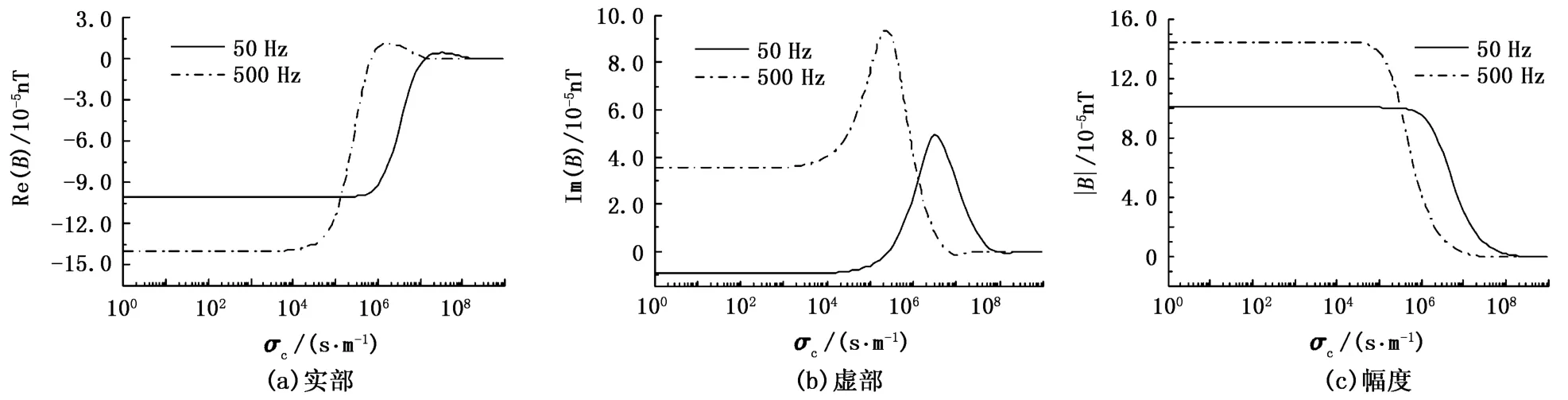
图7 磁感应强度随套管电导率的变化关系Fig.7 Relationship between magnetic induction intensity and casing's conductivity

4 结 论

(1)金属套管的存在导致井间电磁信号的强度变弱，且金属套管对井间电磁信号强度的衰减作用随频率的升高而增大。

(2)金属套管对磁感应强度幅度的影响近似恒定，即有金属套管和无金属套管情况下磁感应强度幅度的比值近似恒定。这个比值取决于金属套管的参数和频率，与地层电导率无关。

(3)当有金属套管存在时，井间磁感应强度的实分量和虚分量除数值发生变化外，还存在“平移”现象且虚分量更加明显，说明金属套管亦引起井间磁感应强度相位的变化。

(4)套管电导率很小时，其对井间电磁信号的影响可以忽略不计。当套管电导率增大到某一临界值时导致井间磁感应强度快速变化。在该临界值处磁感应强度的实分量值快速减小，此后逐渐稳定到一个较低数值，而虚分量则先增加后减小，此后逐渐稳定到一个数值。该临界值与频率有关，频率越高临界值越小。

[1] ALUMBAUGH D L，MORRISON H F.Theoretical and practical considerations for cross-well electromagnetic tomography assuming a cylindrical geometry[J].Geophysics，1995，60(3)：846-870.

[2] LIU C，SHEN L C，ZHANG Y C.Monitoring saltwater injection using conductivity images obtained by electromagnetic cross-hole measurements[J].Radio Science，1995，30(5)：1405-1415.

[3] ZHANG Y C，LIU C，SHEN L C.An iterative algorithm for conductivity image reconstruction from crosswell EM measurements[J].Geophysics，1996，61(4)：987-997.

[4] 魏宝君.三维井间电磁场的联合反演方法[J].石油大学学报：自然科学版，2005，29(3)：20-26.WEI Bao-jun.Combined inversion algorithm of three-dimensional cross-hole electromagnetic fields[J].Journal of the University of Petroleum，China(Edition of Natural Science)，2005，29(3)：20-26.

[5] 魏宝君.井间电磁场的一维、二维联合反演方法[J].地球物理学报，2006，49(1)：264-274.WEI Bao-jun.A combined 1-D/2-D inversion algorithm of cross-hole electromagnetic fields[J].Chinese Journal of Geophysics，2006，49(1)：264-274.

[6] 沈金松，孙文博，赵文杰，等.井间电磁测量数据的模拟与处理解释[J].测井技术，2007，31(5)：417-424.SHEN Jin-song，SUN Wen-bo，ZHAO Wen-jie，et al.Modeling and processing of the cross-hole electromagnetic and measurements and their interpretation[J].Well Logging Technology，2007，31(5)：417-424.

[7] BEER R，ZHANG P，ALUMBAUGH D，et al.Anisotropy modeling and inversions of DeepLook-EM data from Brazil[C/CD].2010 SEG Annual Meeting，October 17-22，2010，Denver，Colorado，USA.

[8] 魏宝君，LIU Q H.水平层状介质中基于DTA的三维电磁波逆散射快速模拟算法[J].地球物理学报，2007，50(5)：1595-1605.WEI Bao-jun，LIU Q H.Fast algorithm for simulating 3-D electromagnetic inverse scattering in horizontally stratified medium via DTA[J].Chinese Journal of Geophysics，2007，50(5)：1595-1605.

[9] 魏宝君，LIU Q H.层状介质中计算体积分方程的弱化BCGS-FFT算法[J].中国石油大学学报：自然科学版，2007，31(1)：49-55.WEI Bao-jun，LIU Q H.Weak-form BCGS-FFT algorithm for volume integral equations in stratified medium[J].Journal of China University of Petroleum(Edition of Natural Science)，2007，31(1)：49-55.

[10] 魏宝君，王颖，王甜甜.电磁波电阻率仪器的基本理论及其在随钻测量中的应用[J].地球物理学进展，2009，24(2)：774-781.WEI Bao-jun，WANG Ying，WANG Tian-tian.The basic theory of electromagnetic wave resistivity instrument and its application to measurement of while-drilling[J].Progress in Geophysics，2009，24(2)：774-781.