AR预测模型的IMM跟踪算法

竹 博，周 游，仵国锋，胡捍英

解放军信息工程大学，郑州 450002

AR预测模型的IMM跟踪算法

竹 博，周 游，仵国锋，胡捍英

解放军信息工程大学，郑州 450002

1 引言

机动目标跟踪已广泛应用于军事和民用领域，近几十年来，人们对该问题进行了广泛而深入的研究。运动模型的建立和滤波过程是机动目标跟踪两个十分重要的过程，其中，滤波过程是建立在目标运动模型的基础上进行的。

针对运动模型的建立，只有当采用的运动模型与目标的运动形式相匹配时，跟踪精度才比较理想。但是机动目标的运动形式不可能始终被单一的运动模型所表征。当前解决目标运动模型不确定的主要方法是交互式多模型滤波算法（IMM）[1-3]，其特点是可以在多个模型之间“转换”，自动调节模型概率，很适合机动目标的跟踪。然而该方法也存在问题：如果模型比较少，不能覆盖目标的运动状态，导致跟踪精度不够；模型数量比较多时，会带来模型间不必要的竞争而使得性能下降。针对滤波过程，经典非线性滤波算法有基于一阶泰勒级数展开的扩展卡尔曼滤波器（EKF）和无迹卡尔曼滤波（UKF）[4-6]。EKF的性能在很大程度上依赖于局部非线性程度，对于强非线性系统的跟踪存在较大误差，而UKF突破传统的随机采样，通过加权采样进行迭代获得参数的最优解，很好解决了非线性滤波问题。在LOS环境下，观测噪声服从高斯分布，UKF可以获得良好的跟踪性能，但是在NLOS环境下，噪声服从非高斯分布[7]，不再符合UKF的高斯假设，造成其跟踪性能明显下降，严重时导致发散。文献[8]提出了一种结合M估计的改进的无迹卡尔曼滤波器，以解决其中的非高斯问题，并取得了良好的性能。

基于以上分析，本文从运动模型的建立和滤波过程分别对传统算法进行改进。首先，针对传统建模方法不能很好地描述目标机动过程导致跟踪性能差的问题，本文利用AR预测模型对具有未知参数的目标运动状态建模，并实时更新目标的运动方程来准确描述目标的运动状态。其次，对于同一个基站，目标在运动过程中的LOS与NLOS状态可能会发生转换，针对传统的滤波算法未考虑这一转换过程导致跟踪性能差的问题，本文利用马尔可夫链来描述LOS与NLOS状态的转换过程，对于LOS状态匹配UKF，对于NLOS状态匹配RUKF。算法首先利用AR预测模型对目标运动状态建模，然后通过IMM方法得到移动台的估计位置，最后利用该位置更新AR预测模型的参数，从而更准确地预测出下一时刻的目标位置。仿真结果表明，在LOS/NLOS混合条件下，该算法能较好地实现对机动目标的鲁棒跟踪。

2 目标跟踪模型

假设移动台的状态向量为 x(n)=[x(n) x˙(n) x¨(n) y(n) y˙(n) y¨(n)]T，分别表示沿x和 y方向的位置、速度和加速度，移动台在n时刻的状态方程如下：

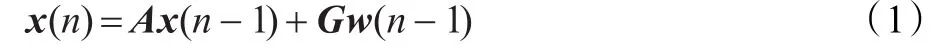
其中，A为状态转移矩阵，w(n)是过程噪声，服从均值为0，方差为σ2w的高斯分布，G为输入矩阵。

在n时刻的观测方程如下：

hm(x(n))表示n时刻移动台与第m个基站的真实距离。M(n)表示n时刻基站与移动台之间的信道状态，观测噪声v(n，M(n))与状态变量 M(n)有关。在LOS状态下，观测噪声服从均值为0，方差为σ2G的高斯分布，而在NLOS状态下，观测噪声服从均值为μ的指数分布[9]，如下式所示：

3 基于AR预测模型的IMM算法

3.1ARIMM算法概述

针对LOS/NLOS混合条件下对机动目标的鲁棒跟踪问题，本文提出一种基于AR预测模型的交互式多模型（IMM）跟踪算法。算法原理框图如图1所示，分为两个模块：AR预测模块和IMM滤波模块。AR预测模块的作用是实时更新目标的运动方程，以匹配目标的真实运动状态。IMM滤波模块的作用是从受噪声污染的观测向量中得到目标的状态信息。IMM的模型集包括LOS和NLOS两种模型，即M=2，模型集的选择具体见3.2节。算法首先将观测向量 y(n)进行交互式多模型滤波，得到状态向量x^(n)，然后通过AR预测模型来更新当前时刻状态方程x(n+1)=Ax(n)+w(n)，从而使得下一时刻的预测值更加逼近实际位置，实现精确跟踪。

图1ARIMM算法原理图

3.2 IMM模型集选择

对于一个基站，移动台处于运动中的LOS与NLOS状态可能会发生变化，状态转换过程服从马尔可夫过程[10]，如图2所示。

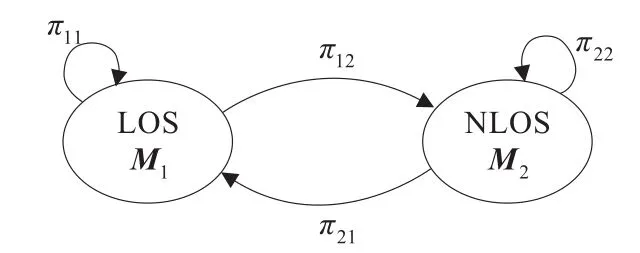
图2 LOS/NLOS马尔可夫转移过程

对于M个基站，就有r=2M种状态，假设不同基站的LOS与NLOS状态转移过程相互独立，此时的一步转移概率矩阵：

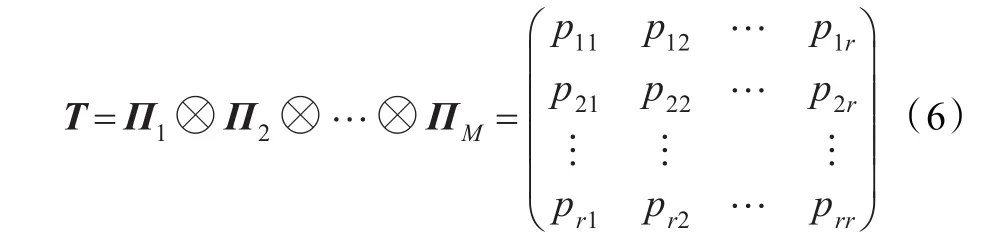
式中，⊗表示Kronecker相乘，Πm表示第m个基站的一步转移概率矩阵。

文献[11]针对M个基站时共有的r=2M种LOS与 NLOS状态组合，例如，M=3时存在M1，M2，…，M8种状态组合，分别为{LOS，LOS，LOS}，…，{NLOS，NLOS，NLOS}。需要对每种组合分别匹配一个EKF进行滤波，以完成目标的跟踪。随着M的增加，计算量呈指数增长，严重影响了跟踪的实时性。为降低计算复杂度，本文采用两种状态：M′1表示所有的基站都处于LOS状态；M′2表示所有的基站都处于NLOS状态。当基站处于 M2，M3，…，Mr-1状态时，状态估计的结果均可以由上述两个状态下的滤波结果线性组合得到。对于M′1状态，匹配UKF进行滤波，此时观测协方差矩阵R(k)= σ2GIM，一步转移概率 p′12=1-p11；对于M′2状态，匹配RUKF进行滤波，观测协方差矩阵R(k)=(σ2G+ μ2)IM，一步转移概率 p′21=1-prr。

3.3 AR预测模型

移动台在n+1时刻的状态方程可以如下表示：

其中，A为状态转移矩阵，w(n)服从均值为0的高斯分布，协方差矩阵为Q，矩阵A和Q可以通过Yule-Walker方程得到[12]。本文仿真部分利用真实 x(n)，n=1，2，3来对算法进行初始化。

算法的初始化(n=1，2，3)：

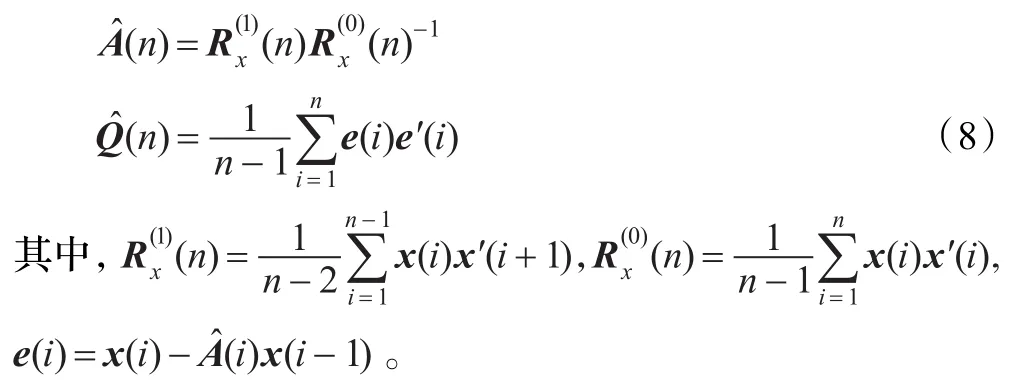
x^(n)是上文中交互式多模型算法（IMM）n时刻的状态估计输出，反过来又更新和。递推估计过程如下(n=4，5，…)：

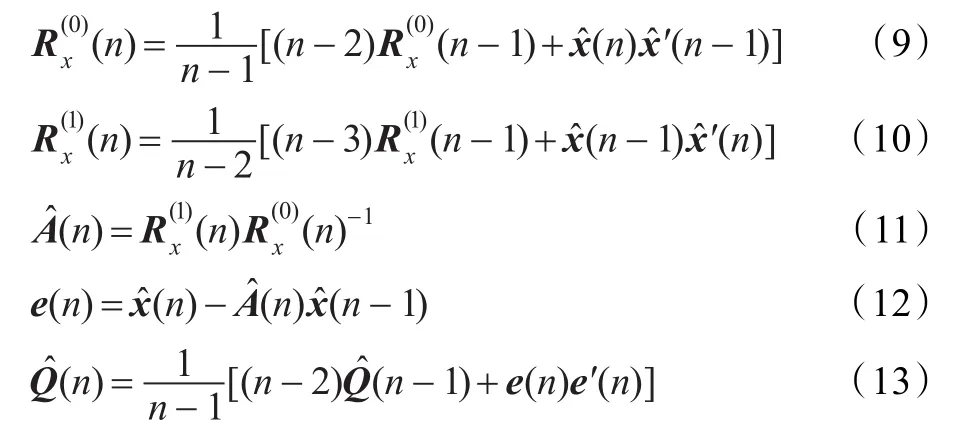
3.4ARIMM算法步骤

ARIMM算法分为以下五个步骤：

步骤1输入交互运算

步骤2模型匹配滤波

在步骤1的基础上，通过模型匹配滤波器，得到各模型的状态估计和协方差估计。LOS状态匹配的是无迹卡尔曼滤波器，NLOS状态匹配的是改进的无迹卡尔曼滤波器。

对于无迹卡尔曼滤波器(j=1)：

式（1）和式（2）可写为Z(n)=D(n)X(n)+V(n)，然后利用改进的无迹卡尔曼滤波方法求出状态估计和协方差矩阵输出为和。

因无迹卡尔曼滤波和改进的无迹卡尔曼滤波比较常见，限于篇幅，在此不做赘述，具体参考文献[6]和文献[8]。

步骤3模型概率的更新

在每一时刻模型概率都必须进行更新，该过程和一般IMM相似。 Λj(n)=N(vj(n);0，Sj(n))，vj(n)为新息，Sj(n)为新息的协方差矩阵。

步骤5运动模型参数估计

4 仿真实验及分析

仿真1针对移动台匀速直线运动，未发生机动时，分别在不同噪声环境下对UKF，RUKF，IMM算法进行仿真实验，并对其性能进行分析。

仿真结果如图3～图5。其中，图3是当ε=0时，即三个基站都处于LOS状态时UKF，RUKF，IMM三种算法的跟踪性能，图4是当ε=0.25时三种算法的跟踪性能，图5是当ε=0.5时三种算法的跟踪性能。文献[13]指出当污染度高于50%时，RUKF算法达到“溃点”，带来跟踪性能的严重下降，故本文未对污染度高于50%的情况进行仿真。从仿真结果可以看出：当所有基站都处于LOS状态时，UKF算法的跟踪精度最高，其次是IMM和RUKF算法；当污染度ε=0.25时，IMM算法的跟踪精度最高，其次是RUKF和UKF算法：当污染度ε=0.5时，RUKF算法的跟踪精度最高，其次是IMM和UKF算法。从理论上分析，当观测噪声服从高斯分布时，无迹卡尔曼滤波器能获得最优估计，性能比较好。而当噪声服从非高斯分布时，无迹卡尔曼滤波器的性能会变差，鲁棒无迹卡尔曼滤波由于采用了M估计，可以有效减弱或消除观测值中粗差的影响，达到较好的跟踪效果。而本文的交互式多模型算法正是结合了这两种滤波器的优点，在污染度小的情况下，UKF对精度的提高起主要作用，在污染度大时，RUKF对粗差影响的减弱起主要作用，因此在LOS/NLOS混合条件下实现了对机动目标的跟踪精度与鲁棒性的良好折中。

图3 污染度ε=0时三种算法性能

三种算法的平均跟踪误差如表1所示，在低污染度(ε=0)时，IMM算法和UKF算法性能相当；在ε=0.25时，IMM算法性能明显优于UKF和RUKF；在高污染度(ε=0.5)时，IMM算法和RUKF算法性能相当。可以看出，在不同的污染度下，IMM算法都能保持良好的跟踪性能，因此，与传统的UKF和RUKF算法相比，该算法有更好的鲁棒性。

图4 污染度ε=0.25时三种算法性能

图5 污染度ε=0.5时三种算法性能

仿真2针对移动台发生机动时，在LOS/NLOS混合条件下对IMM和ARIMM算法进行仿真实验，并对其性能进行分析。

移动台的运动轨迹如图6中实线所示。在运动的过程中，对于LOS状态，观测噪声服从均值为0，方差σ2w=602的高斯分布，对于NLOS状态，观测噪声服从均值μ=100的指数分布，观测值的污染度ε=0.25。从图7可以看出，当移动台发生机动时，ARIMM算法的平均误差为33 m，而IMM算法的平均误差为107 m，ARIMM的跟踪性能更好，从理论上分析，ARIMM算法通过迭代的思想不断更新AR预测模型中的参数，从而使AR模型与真实运动状态更匹配，实现精确跟踪；而IMM算法中，状态方程是恒定的，当移动台发生机动时，运动状态不再符合初始的状态方程，就会导致下一时刻的预测值严重偏离真实位置，从而导致跟踪性能的下降。

图6 移动台真实轨迹和估计轨迹

表1 UKF、RUKF、IMM三种算法平均跟踪误差比较m

图7 两种算法的误差性能

下面来分析算法的计算效率，仿真计算机的配置如下：CPU为Intel®奔腾®4 2.8 GHz内存为1 GB，操作系统为Windows XP，仿真软件为MATLAB R2006。UKF、RUKF、IMM和ARIMM四种算法仿真所需的时间如表2所示。

表2 不同滤波算法计算时间

从表2可以看出，UKF的运算时间最少，单次运行时间为43.572 2 ms。RUKF由于其采用了M-估计，增加了运算量。而IMM算法由于并行使用了UKF和RUKF算法，使其运算量大大增加。本文的ARIMM算法和IMM算法区别在于，IMM算法中使用恒定的状态模型，而ARIMM算法中使用了AR预测模块实时更新目标的运动状态，导致本文算法的运算时间比IMM有所增加。由于文中的AR预测模型为一阶，当前时刻的状态更新仅与上一时刻有关，运算过程和IMM算法中的交互、滤波模块相比运算简单，因此本文算法的运算时间较IMM算法稍有增加，大约增加了7%，这对现有的硬件条件是可以接受的。综合跟踪精度和运算量考虑，ARIMM算法是一种在LOS/NLOS混合环境下的有效跟踪算法。

5 结束语

针对LOS/NLOS条件下对机动目标的鲁棒跟踪，提出一种基于AR预测模型的IMM跟踪算法。该算法利用AR预测模型描述目标的运动状态，通过并行使用UKF和RUKF完成滤波，充分发挥了无迹卡尔曼滤波和改进的无迹卡尔曼滤波的优点，在LOS/NLOS混合条件下实现了对机动目标的鲁棒跟踪，最后通过仿真验证了所提算法的有效性。

[1]Seah C E，Hwang I.Algorithm for performance analysis of the IMM algorithm[J].IEEE Transon Aerosp Electron Syst，2011，47（2）：1114-1124.

[2]Foo P H，Ng G W.Combining the interacting multiple model method with particle filters for manoeuvring target tracking[J].IEEE Trans on Radar，Sonar and Navigation，2011，5（3）：234-255.

[3]Farrel W.Interacting multiple model filter for tactical ballistic missile tracking[J].IEEE Trans on Aerosp Electron Syst，2008，44（2）：418-426.

[4]Kay S.Fundamentals of statistical signal processing：estimation theory[M].Englewood Cliffs，NJ：Prentice-Hall，1993.

[5]Gustafsson F，Hendeby G.Some relation between extend and unscend kalman filter[J].IEEE Trans on Signal Processing，2012，60（2）：545-555.

[6]Liu Changyun，Shui Penglang.Unscented extended Kalman filter for target tracking[J].IEEE Journal of Systems Engineering and Electronics，2011，22（2）：188-192.

[7]Gezici S，Sahinoglu Z.UWB geolocation techniques for IEEE 802.15.4a personal area networks[R].Cambridge，MA，2004.

[8]Wang X，Cui N.Huber-based unscented filtering and its application to vision-based relative navigation[J].IET Radar，Sonar and Navigation，2010，4（1）：134-141.

[9]Guvenc I，Chong Chia-Chin.A survey on TOA based wireless localization and NLOS mitigation techniques[J].IEEE Communication Surveys and Tutorials，2009，11（3）：107-124.

[10]Li Wenling，Jia Yingmin.Location of mobile station with maneuvers using an IMM-based cubature kalman filter[J]. IEEE Trans on Industrial Electronics，2012，59（11）：4338-4348.

[11]Fritsche C，Hammes U.Robust mobile terminal tracking in NLOS environment using IMM[C]//ICASSP，2009：3049-3052.

[12]Lim J S，Oppenheim A V.Advanced topics in signal processing[M].[S.l.]：Prentice Hall，1987.

[13]Cover T M，Thomas J A.Elements of information theory[M]. New York：Wiley，1991.

ZHU Bo,ZHOU You,WU Guofeng,HU Hanying

PLA Information Engineering University,Zhengzhou 450002,China

In view of the problem of robust tracking of maneuvering target under LOS/NLOS condition,an IMM algorithm based on AR prediction model is proposed（ARIMM）.AR prediction model is adopted to model the motion state, and UKF and RUKF are utilized separately for the reason that the state LOS and NLOS have different distribution of observation noise,and the IMM filter is used to estimate the position of BS,and the position is used to update the current parameters in AR prediction model and the AR model is made more matched with the true motion state,therefore the algorithm can perform precisely tracking.Simulation result demonstrates that the proposed algorithm performs better robustness under LOS/NLOS condition compared with the traditional UKF and RUKF.

maneuvering target tracking;Interacting Multiple Model（IMM）;Auto Regressive（AR）prediction model; Unscented Kalman Filter（UKF）

针对LOS/NLOS混合条件下对机动目标的鲁棒跟踪问题，提出一种基于AR预测模型的交互式多模型（Interacting Multiple Model，IMM）跟踪算法（ARIMM）。该算法利用AR预测模型对运动状态建模，针对LOS与NLOS条件下观测噪声的分布不同分别使用无迹卡尔曼滤波器（Unscented Kalman Filter，UKF）和改进的无迹卡尔曼滤波器（Robust Unscented Kalman Filter，RUKF），通过IMM方法估计出移动台的位置，利用该位置更新AR模型的参数，使AR模型与真实运动状态更加匹配，实现精确跟踪。仿真结果表明，在LOS/NLOS混合条件下，与传统的UKF和RUKF算法相比，该算法对机动目标跟踪的鲁棒性更好。

机动目标跟踪；交互式多模型；自回归（AR）预测模型；无迹卡尔曼滤波器

A

TN925

10.3778/j.issn.1002-8331.1302-0129

ZHU Bo,ZHOU You,WU Guofeng,et al.AR prediction model based IMM tracking algorithm.Computer Engineering and Applications,2014,50（24）：222-226.

国家科技重大专项（No.2011ZX03003-003-02）。

竹博（1988—），男，硕士研究生，主研方向为蜂窝网定位。E-mail：zhuboapple@163.com

2013-02-22

2013-04-07

1002-8331（2014）24-0222-05

CNKI网络优先出版：2013-04-10，http∶//www.cnki.net/kcms/detail/11.2127.TP.20130410.1554.002.html

◎工程与应用◎