平移不变小波在心音信号去噪中的应用
郭兴明,何彦青,卢德林,袁志会
重庆大学 生物工程学院,重庆 400044
平移不变小波在心音信号去噪中的应用
郭兴明,何彦青,卢德林,袁志会
重庆大学 生物工程学院,重庆 400044
1 引言
心音反映了心脏及心血管系统的生理和病理特征[1],是一种重要的生理信号,在心脏疾病诊断中具有重要意义。心音在采集过程中难免会引入噪声,包括环境噪声、工频噪声、采集设备与皮肤间的摩擦声以及仪器本身的声音等[2]。噪声将影响心音信号的分析,从而对心脏疾病的诊断构成潜在威胁。因此在心音信号分析之前,需先对其进行去噪处理。
1995年,Donoho D.L.和Johnstone[3-4]提出了小波阈值去噪方法,把小波系数中绝对值较小的看成噪声对应的小波系数,置为零;绝对值较大的看成信号对应的小波系数,将其保留或者收缩,得到估计小波系数,最后利用估计小波系数重构信号以实现去噪。以此为基础,相关学者进行了进一步的探索与改进[5-7],使得小波阈值去噪方法逐渐完善。小波变换具有多尺度多分辨的特性和良好的时频局部化分析能力,可较好地抑制噪声,提取目标信号的瞬态、稳态信息及波形特征[8],在各种类型信号的去噪研究中得到了广泛应用[9-10]。
心音信号是一种非平稳信号,加上采集过程中噪声的引入,使得原信号与其小波分解细节信号中往往存在着一些变化较为剧烈的点,这类常用Lipschitz指数[11]描述信号局部奇异性的点称为奇异点。通过小波分解与重构可以较精确地检测到信号奇异点的位置[12]。而小波变换的局部化特性会造成小波去噪后在信号的不连续点处产生振荡,产生显著的Pesudo-Gibbs效应,影响去噪效果。由于产生的振荡幅度与不连续点的位置密切相关,因此本文采用平移不变小波去噪方法[13-14]通过对信号序列平移来改变奇异点在整段信号的位置,从而降低或消除振荡[15-16]。实验结果表明,与传统小波软阈值去噪法相比,该方法能消除Pesudo-Gibbs振荡现象,在较好地保留信号细节特征的同时,使信号的信噪比和根均方误差得到了明显改善,获得了更好的去噪效果。
2 平移不变小波去噪原理
针对传统小波软阈值去噪的缺陷,采用对原信号和小波变换所得低频信号进行循环平移的方法来改变不连续点的位置,然后对平移后的信号进行阈值去噪处理,得到近似估计信号,对估计信号重构就可得到最后的去噪结果。
2.1 快速TI前向小波分解
对信号进行平移不变前向小波分解时,首先将原信号进行平移,然后分别将原信号和平移后的信号分解为低频部分和高频部分,再将低频信号进行平移,并对低频信号和平移后的低频信号进一步分解,这样逐级分解下去。图1为TI前向小波分解过程,为2层分解,图中βJ,0表示原信号,α和其他 β分别表示高频和低频,每一级分解后的系数均直接存入TI表中,并将每一级的低频系数存入TI表中,置于第一列,到下一级时再将其更新,直至将最后一级的低频系数存入,则不再发生变化。

图1 TI前向小波分解过程
定义Sh为对信号xi(0≤i≤n)进行h位循环平移,其逆表示为Sh
-1=S-h(h∈H),平移量H最大为原信号长度n。令 βJ,0=xi,设(h-,g-)表示正交小波的分析滤波器,n=2J,j=J-1,J-2,…,J-L,L表示分解级数,计算原信号 S0βJ,0及其循环平移h位的信号ShβJ,0的离散小波变换(Discrete Wavelet Transform,DWT),如图2所示。

图2 离散小波分解过程
小波变换通过函数dwt实现,其延拓方式设为周期型以保证分解后系数的总数目不变。信号经离散小波变换后得到低频系数 βj,k与小波系数αj,k。
对各分辨级上的低频信号进行平移,并在每个分解级对低频信号 S0βj,k和平移后的低频信号 Shβj,k重复这一小波变换过程,即可得到所有可能的小波系数。
最后所得到TI变换的结果为:
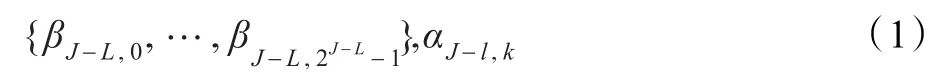
其中l=1,2,…,L;k=0,1,…,2l-1,对每个0≤k<2l,αJ-l,k中包含2J-l=n/2l个小波系数,因此TI变换的小波系数共为n(L+1)。
TI变换数据可以存放在一个TI表中。该表由n行 l+1列构成,第1列存放 n个低频系数 βJ-L,0,…,βJ-L,2J-L-1。第 l+1(l=1,2,…,L) 列顺次存放第 l次小波分解得到的小波系数αJ-l,k(k=0,1,…,2l-1),该列可看成2l个盒子,每个盒子存放2J-l=n/2l个小波系数。
2.2 阈值选取
除TI表的第1列中的所有低频系数保持不变外,将其余各列的小波系数按照软阈值法进行处理。利用其余每一列的小波系数对噪声的标准差σl做出估计,将该列小波系数的阈值定义为 λl=σl,其中σl= median|αJ-l,k|/0.674 5(k=0,1,…,2l-1)。
2.3 TI变换的快速重构
重构过程如图3所示,从 j=J-L开始,对每个k(0≤k<2j)计算:

当对分辨率 j对应的所有k计算结束后,置 j=j+1。重复上述计算过程直到 j=J。

图3 TI变换重构示意图
在各个分辨级上,分别从TI表中取出低频系数和小波系数,用周期延拓的离散小波逆变换进行重构。同时,对序列进行反向平移,用每一级重构出的低频系数更新TI表的第一列,直至得到最终的重构信号,则该信号正是所有循环平移去噪信号的平均信号。
平移不变小波去噪算法流程如图4所示。

图4 平移不变小波去噪算法流程图
3 结果与分析
3.1 信号来源
应用重庆博精医学信息研究所研制的“运动心力监测仪”(ECCM,专利号01256971.2,第一代产品注册证号:渝药管械(试)字99第220007)在重庆医科大学附属第一医院采集心音信号,采样频率为11 025 Hz,量化值为8 bit,采集的信号最终以wav格式进行保存。
3.2 去噪结果对比
本文采用小波软阈值去噪法和平移不变小波去噪法分别对加噪后的心音信号和实际采集的心音信号进行处理,并对去噪结果进行对比分析。
(1)选择1例不含噪声的纯净心音信号(n=512),如图5(a),利用Matlab中的randn随机函数给纯净信号叠加上白噪声,加噪后的心音信号如图5(b)所示。选择sym8为小波基,对加噪信号做五层分解处理,采用小波软阈值去噪法和平移不变小波去噪法(H=H512(0≤h≤512))的心音信号进行去噪处理,去噪结果分别如图6(a)、(b)所示。对比可知,小波软阈值去噪后,图6(a)在i=330和i=350附近的局部区域,信号产生了明显的变化。

图5 纯净心音信号及加噪后的信号

图6 纯净心音加噪后的去噪结果
采用信噪比(SNR)和根均方误差(RMSE)评价两种方法在不同噪声信噪比水平(SNR=1、3、5、7)下的去噪效果,比较结果如表1、表2所示。
根均方误差定义为:
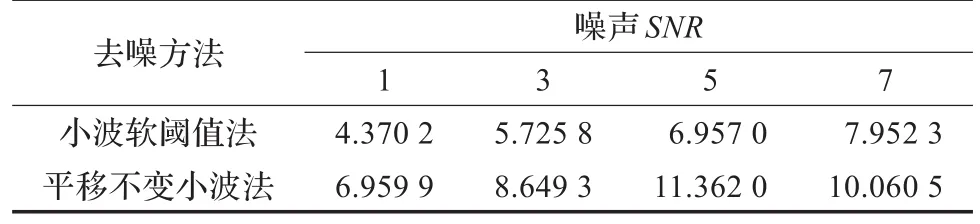
表1 两种方法去噪后信号SNR对比 dB
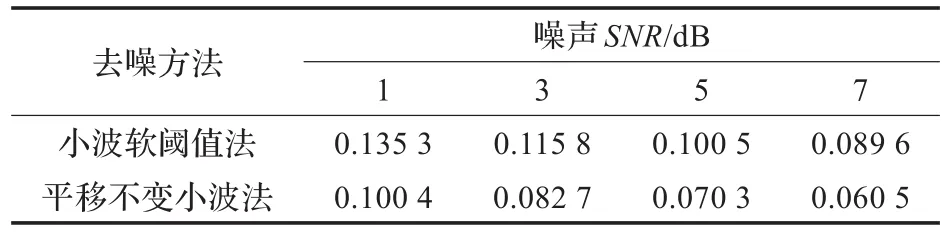
表2 两种方法去噪后信号RMSE对比

其中xi为不含噪声的纯净心音信号,yi为去噪处理后的心音信号。
根均方误差反映了去噪处理后信号与原始纯净信号的吻合程度,RSME值越小,表示二者的吻合程度越高,去噪处理的效果越好。
从表1、表2可以看出,与小波软阈值去噪法相比,平移不变小波去噪法使得信噪比得到了明显的提高,同时根均方误差也明显减小。
(2)由于实际采集的心音信号还包含呼吸、体动和直流偏置等成分,使波形含有噪声和趋势项,如图7(a)所示(n=4 096)。首先采用多项式最小二乘法对实际信号进行趋势项消除操作,结果如图7(b)所示。然后分别采用小波软阈值法和平移不变小波去噪法H=H4096(0≤h≤4 096)对趋势项消除后的心音信号进行去噪处理,结果如图8(a)、(b)所示。

图7 实际采集的心音信号

图8 实际采集心音信号的去噪结果
从图8中可以看出,平移不变小波去噪法使得小波软阈值去噪产生的振荡现象得到了有效抑制,且在较好地保留原始信号细节特征的基础上很好地消除了心音信号包含的噪声,去噪效果明显优于传统软阈值去噪法。
4 结论
本文利用平移不变小波去噪的方法对心音信号进行去噪处理,当信号包含多个奇异点时,选定的平移量对一个奇异点最佳,对另一个也可能最差,采用在一定范围内循环平均的方法则可以有效避免这种情况。为了更好地消除振荡效应,本文采用完全平移不变小波去噪方法,即将平移量选择为H=Hn(0≤h≤n)。该方法不需预先确定平移量范围,可根据信号长度自动完成整个运算,计算量为nln(n)。文中的结果显示该方法能有效去除心音信号中的噪声信号,且信噪比得到很大提高,较好恢复了信号的原始形态。该方法弥补了传统小波阈值去噪的不足,消除了在奇异点附近产生的振荡现象,能够满足心音信号预处理的要求,为心音信号的进一步分析奠定了基础。
[1]罗健仲,罗琳.心脏听诊[M].5版.北京:人民卫生出版社,2000:27-35.
[2]吴延军,徐泾平,赵艳.心音的产生与传导机制[J].生物医学工程学杂志,1996,13(3):280-288.
[3]Donoho D L,Johnstone I M.Ideal spatial adaptation via wavelet shrinkage[J].Biometrika,1994,81(12):425-455.
[4]Donoho D L.De-noising by soft-thresholding[J].IEEE Trans on Information Theory,1995(3):613-627.
[5]王宏强,尚春阳,高瑞鹏,等.基于小波系数变换的小波阈值去噪算法改进[J].振动与冲击,2011,30(10):165-168.
[6]刘真,杨大成,王欣.基于双Haar小波软阈值去噪的阈值选取[J].山东大学学报:工学版,2004,34(6):32-35.
[7]Chang Fengxiang,Hong Wenxue,Zhang Tao.Research on wavelet denoising for pulse signal based on improved wavelet[C]//2010 First International Conference on Pervasive Computing,Signal Processing and Applications,2010:564-567.
[8]孙延奎.小波分析及其应用[M].北京:机械工业出版社,2005:100-152.
[9]吕立蕾,龚威,宋沙磊,等.地物反射率探测激光雷达回波信号的小波去噪[J].武汉大学学报,2011,36(1):56-59.
[10]朱冰莲,刘倩.心音信号的自适应小波去噪[J].计算机技术与发展,2006,16(10):83-84.
[11]张引红,吴胜举.鼾音信号奇异点检测的小波变换分析方法[J].计算机工程与应用,2008,44(5):232-234.
[12]魏阿妮,严碧歌.心音信号奇异点的小波分析方法[J].现代生物医学进展,2010,10(23):4574-4577.
[13]Coifman R R,Donoho D L.Translation invariant denoising[J].Wavelets and Statistics,1995,103:125-150.
[14]汤宝平,杨昌棋,谭善文,等.基于平移不变的小波去噪方法及应用[J].重庆大学学报:自然科学版,2002,25(3):1-5.
[15]姜长泓,王龙山,尤文,等.基于平移不变小波的声发射信号去噪研究[J].仪器仪表学报,2006,27(6):607-610.
[16]Ren Zhong,Liu Guodong,Zeng Lvming,et al.Research of the bio-chemical spectrum denoise based on a novel wavelet threshold function and an improved translationinvariance method[C]//Seventh International Conference on Photonics and Imaging in Biology and Medicine,2009,7280.
GUO Xingming,HE Yanqing,LU Delin,YUAN Zhihui
College of Bioengineering,Chongqing University,Chongqing 400044,China
The wavelet threshold de-noising method can eliminate the noise existing in heart sound signals,but the lack of translation invariance,may produce artificial oscillation phenomenon near the singularity of the signal,namely Pesudo-Gibbs phenomenon influencing the de-noising result.Therefore,the wavelet threshold de-noising method based on translation invariance(Translation Invariance,TI)is adopted to process the heart sound signals,which changes the position of singular points through translating the signal sequence,to reduce or eliminate the oscillation.Before processing heart sounds with this way,firstly it needs to eliminate the interference introduced during the acquisition process by reducing trend terms. The experimental results show that this method eliminates artificial oscillation phenomenon,and that the Signal-to-Noise Ratio(SNR)and Root Mean Square Error(RMSE)are obviously improved under the precondition of keeping the main characters of the heart sound signals.
heart sound signals;wavelet threshold de-noising;translation invariance
小波阈值去噪方法可以消除心音信号中的噪声,但其缺乏平移不变性,可能在信号的奇异点附近产生人为的振荡现象,即Pesudo-Gibbs现象,影响去噪效果。采用平移不变(Translation Invariance,TI)小波阈值去噪的方法对心音信号进行去噪,通过对信号序列平移来改变奇异点在整段信号的位置,以降低或消除振荡。对信号采用平移不变小波去噪之前,先通过消除趋势项来降低信号采集过程中引入的干扰。实验结果表明,该方法消除了人为振荡现象,在保留心音信号主要特征的前提下,信号的信噪比(Signal-to-Noise Ratio,SNR)和根均方误差(Root Mean Square Error,RMSE)均得到明显改善。
心音信号;小波阈值去噪;平移不变性
A
R318;TP391
10.3778/j.issn.1002-8331.1301-0364
GUO Xingming,HE Yanqing,LU Delin,et al.Application of translation invariant wavelet in heart sound signal de-noising.Computer Engineering and Applications,2014,50(24):209-212.
国家自然科学基金(No.30770551);重庆市新型医疗器械重大科技专项(CSTC,2008AC5103)。
郭兴明(1964—),男,教授/博导,主要研究方向为生物医学电子与信息技术;何彦青(1989—),硕士研究生,主要研究方向为生物医学信息检测及处理。E-mail:guoxm@cqu.edu.cn
2013-01-31
2013-05-02
1002-8331(2014)24-0209-04

