压缩感知分组分离语音增强

宁矿凤，王景芳

湖南涉外经济学院 信息科学与工程学院，长沙 410205

压缩感知分组分离语音增强

宁矿凤，王景芳

湖南涉外经济学院 信息科学与工程学院，长沙 410205

1 引言

语音是非平稳、时变的信号。通过语音传递信息是人类最重要、最常用的信息交换形式之一。通常，研究者们是在语音信号相对纯净的条件下，对信号进行各种处理。但现实生活中的语音不可避免地要受到周围环境噪声的影响。这些噪声的存在会严重影响语音信号的质量与可懂度。在这种实际需要的推动下，早在20世纪60年代，语音增强这个课题作为语音信号处理的一个重要分支就已经引起了人们的注意；20世纪70年代曾形成了一个研究高潮，并取得了一些基础性成果。目前，语音增强[1]方法主要有谱减法、Weiner滤波、Kalman滤波，以及相继发展起来的子空间增强、小波变换和这些增强方法的各种改进算法。

语音增强是语音处理的一项重要技术，在语音识别、语音编码、语音合成等领域中有着广泛的应用。语音增强的目的是从带噪语音中提取尽可能纯净的原始语音。但由于噪声信号都是随机产生的，完全消噪几乎不可能。因此，实际语音增强的目标主要有：提高语音清晰度，改善语音质量；提高语音可懂度[2]，方便听者理解。

传统的奈奎斯特采样定理要求采样率不小于信号最高频率的两倍，随着信号处理技术的发展和被处理数据量的激增，这种采样方法已远远不能跟上高速信号处理的要求。2006年，Donoho等提出了压缩感知（Compressed Sensing，CS）理论[3-5]，对于具有稀疏性的信号，可以利用其稀疏特性，以少于信号采样点的点数就可以近似恢复原信号。这一理论大大推动了信号处理理论的进程，具有广阔的应用前景。目前，压缩感知理论在压缩成像、模拟信息转换、生物传感、信号检测与分类、无线传感器网络、数据通信和地球物理数据分析等领域都有很好的应用[6]。

压缩感知理论同样可以应用于语音信号。语音信号在某些变换域上具有稀疏性，如所熟知的傅里叶变换（FFT）、DCT变换与小波变换等，但是，目前关于语音信号处理的压缩感知研究并不多，尚属于起步阶段。Griffin等在多通道语音信号处理中应用了CS理论[7]，Giacobello等将CS理论应用于语音编码[8]，Sreenivas和Kleijn认为[9]CS在语音信号中的应用尚未开发，关于语音信号稀疏域和稀疏度的研究也不够深人，而且，由于基本的CS计算运算量非常大，重构语音信号的感知特性如何和计算量的大小也是实际应用中需要着重考虑的问题。在国内，南京邮电大学的杨震等[10-17]将CS理论与语音信号相结合，开展了关于观测矩阵、稀疏变换矩阵、语音端点检测、说话人识别系统抗噪等方面的研究。这些都表明CS理论与语音信号处理技术相结合具有广阔的研究前景。

语音信号作为一种特殊的信号，如何利用语音信号自身的特点，寻找能更好地对语音信号进行稀疏化的变换方法，以得到更高的信噪比，正是本文将要研究的内容。本文研究了一种压缩感知分组分离语音增强方法，这项研究把信号去噪与稀疏性信号重构结合起来，经过多种噪声环境测试效果良好。

2 压缩感知原理

2.1 压缩感知表述

压缩感知理论主要思想是：假设一长度为N的信号x在某个正交基或紧框架Ψ上的系数是稀疏的（即只有少数的非零系数），若把其系数投影到另一个与变换基Ψ不相关的观测基Φ∶M×N，M＜＜N上，得到观测集合 y∶M×1。那么信号x可以凭借这些观测值通过求解一优化问题而精确恢复。CS理论框架如图1所示。

CS理论是一种新的在采样的同时实现压缩目的理论框架，它的压缩采样过程如图1所示。首先，如果信号 x∈RN在某个正交基或紧框架Ψ上是可压缩的，求出变换系数θ=ΨTx，θ是x的等价或逼近的稀疏表示；第二步，设计一个平稳的、与变换基Ψ不相关的M×N维的观测矩阵Φ，将θ投影到M维空间，得到观测集合y=Φθ=ΦΨTx，该过程也可以表示为信号x通过矩阵ACS进行非自适应观测：y=ACSx（其中ACS=ΦΨT），ACS称为CS信息算子[5]；最后，利用下面的优化问题求解x的精确或近似逼近x^：

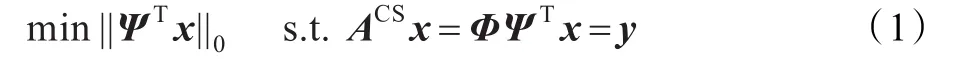
求得的向量x^在基Ψ上的表示最稀疏。

CS理论主要涉及以下几个方面的内容：（1）对于信号x∈RN，如何找到某个正交基或紧框架Ψ，使其在Ψ上是可压缩的，即信号的稀疏表示问题。（2）如何设计一个平稳的、与变换基Ψ不相关的M×N维的观测矩阵Φ，保证稀疏向量θ从N降维到M时重要信息不遭破坏，即信号低速采样问题。（3）如何设计快速重构算法，从一个非常少的线性观测Y=ACSX中恢复信号，即信号重构问题。

在信号x可压缩的前提下，求解欠定方程组y=ACSx的问题转化为最小l0范数式（1）问题，它需要列出X中所有非零项位置的CKN种可能的线性组合。因此，求解式（1）的数值计算极不稳定而且是NP难问题。Chen，Donoho和Saunders指出，求解一个更加简单的l1优化问题会产生同等的解（要求Φ和Ψ不相关）：

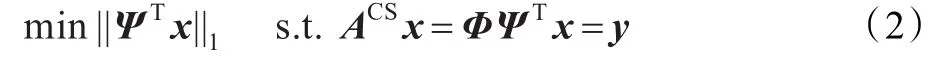
稍微的差别使得问题变成了一个凸优化问题，于是可以方便地化简为线性规划。

2.2 含噪信号的恢复问题

在实际的工程应用中，待处理信号一般都不同程度地受到各种噪声的污染。这时含噪信号不是严格的稀疏信号，但是仍属于可压缩信号。现有的压缩感知理论中，恢复信号的最基本依据是信号在某个变换空间的分解系数是稀疏的，而噪声的存在则破坏了信号在空间中的稀疏性。在使用优化方法恢复信号时，如果对含噪信号采用单一的稀疏性约束原则，则无法有效恢复原始稀疏信号。压缩感知理论仍然可以采用其他的有效恢复信号方法，主要的不同之处在于恢复过程所使用的优化目标函数的不同形式和参数设置，不同的优化目标函数使得信号的恢复效果也不尽相同。

在含噪信号的恢复过程中沿用基追踪（Basis Pursuit，BP）方法中对噪声的抑制方法，主要针对的是信号中的噪声分布已知的情况。

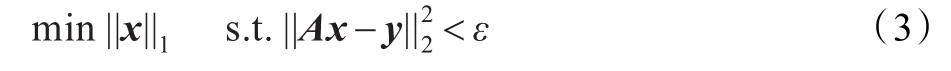
当已知信号的稀疏程度（l1范数大小）时，可采用LASSO方法来对信号进行有效恢复[18]：

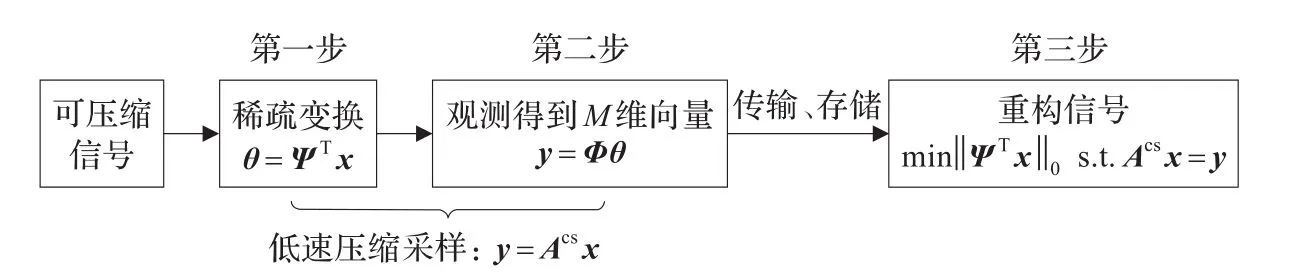
图1 CS理论框架

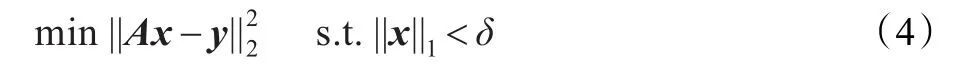
当对信号和噪声都是未知时，把寻找稀疏解问题归结为带约束二次规划（BSQP）问题。

3 分组分离压缩感知信号重构算法设计

（1）含噪信号的恢复问题（5）的分组分离[19]：

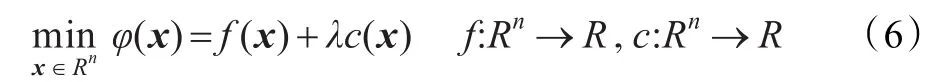
式（6）的求解，可化为式（7）迭代，{xt，t=0，1，…}，αt＞0，∇f为梯度。

（5）用 ym(i)，sm(i)和dm(i)分别表示第m帧时刻i的带噪语音、纯净语音和加性噪声。假设纯净语音信号与噪声互不相关，有

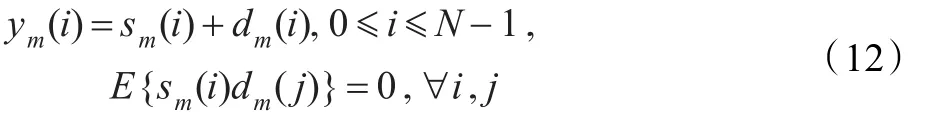
对上式进行FFT变换，有

其中，Ym(ω)，Sm(ω)与Dm(ω)分别表示向量 ym，sm和dm的FFT变换。

在式（6）中，y=Φym，ym为第m帧时域带噪语音信号，y是压缩投影信号，A=ΦΨT，所求x为压缩感知与软阈值式（9）去噪[20]重构语音频谱：(ω)=x⇒(i)= F-1{(ω)}=ΨTx。去噪强弱由初始λ决定，软阈值去噪理论分析参见文献[20]。

4 实验测试评估

背景噪声选自AURORA库[22]与Noisex-92数据库[23]，纯净语音“The birch canoe slid on the smooth planks.”文件sp01.wav[22]，采样频率 fs=8 kHz。在语音分帧过程中，帧长取25 ms，即帧长M=0.025 fs=0.025×8 000= 400点，帧移M/2，每帧分16组，每组取2阶范数ci(z)=||z||2。

采用信噪比：

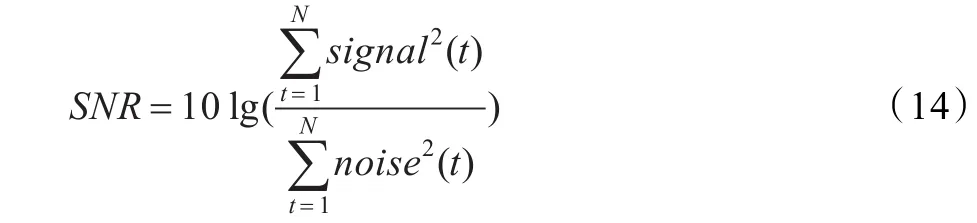
来定量地分析算法的去噪效果。客观上从语音波形、语谱图、信噪比、分段信噪比（Time-domain segmental SNR（dB），－10＜SNRseg＜35）、感知语音质量评价[23-26]（Perceptual Evaluation of Speech Quality，1＜PESQ＜4.5）与可懂度fAI[27]提高等几个方面对本文算法的性能进行了综合分析。

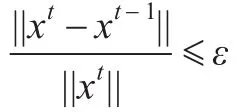
实验1选取噪声源——白噪声（white）频率混在语音频段，本文算法达到了预期效果。图2为压缩感知语音增强前后结果对比。

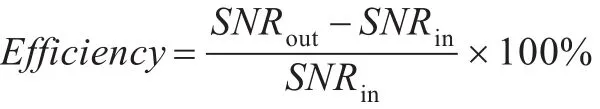
图2 压缩感知语音增强前后结果对比

实验2用本文压缩感知语音增强，在同语音加载不同噪声背景：白噪声（white）、粉色噪声（pink）、航空噪声（f16）、工厂噪声（factory）与人的嘈杂声（babble）在信噪比SNR=5 dB时比较，波形与语谱图比较结果见图3，考查算法的实时跟踪结果。

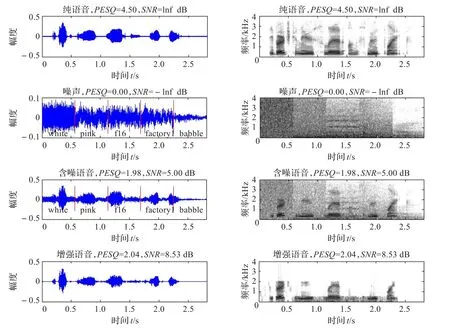
图3 SNR=5 dB下同一语音不同噪声下语音增强方法的波形与语谱图比较

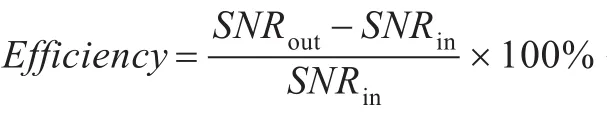
5 结论

本文研究了一种软阈值分组分离压缩感知含噪语音增强方法，语音信号的稀疏表达设计为快速傅里叶变换，观测矩阵设计为一复数矩阵式（11），信号压缩重构结合二阶范数的分组分离逼近稀疏重建（Sparse Reconstruction by Separable Approximation，SpaRSA）方法。实验表明，本文提出的算法尽管fAI没得到改善，但含噪信号压缩重构，信噪比提高幅度较大，PESQ也明显得到改善，能更有效地抑制背景噪声。这开创了语音增强方法新的途径，并为语音稀疏采样与重构开拓了新视野，有着广泛的应用前景。

[1]Loizou P C.Speech enhancement：theory and practice[M]. USA：CRC Press，2007.

[2]Loizou P C，Kim G.Reasons why current speech-enhancement algorithms do not improve speech intelligibility and suggested solutions[J].IEEE Transactions on Audio，Speech，and Language Processing，2011，19（1）：47-56.

[3]Donoho D.Compressed sensing[J].IEEE Trans on Information Theory，2006，52（4）：1289-1306.

[4]Baraniuk R G.Compressive sensing[J].IEEE Signal Processing Magazine，2007，24（4）：118-121.

[5]Donoho D，Tsaig Y.Extensions of compressed sensing[J]. Signal Processing，2006，86（3）.

[6]石光明，刘丹华，高大化，等.压缩感知理论及其研究进展[J].电子学报，2009，37（5）：1070-1081.

[7]Griffin A，Tsakalides P.Compressed sensing of audio signals using multiple sensors[C]//Proc 16th European Signal Processing Conference（EUSIPCO’08），Lausanne，Switzerland，2008.

[8]Giacobello D，Christensen M G，Murthi M N，et al.Retrieving sparse patterns using a compressed sensing framework：applications to speeeh coding based on sparse linear prediction[J].Signal Processing Letters，2010，17（l）：103-106.

[9]Sreenivas T V，Kleijn W B.Copressive sensing for sparsely excited speech signal[C]//Proceedings of the 2009 IEEE International Conference on Acoustics，Speech and Signal Processing，Taipei，Taiwan，China，2009：4125-4128.

[10]郭海燕，杨震.基于近似KLT域的语音信号压缩感知[J].电子与信息学报，2009，31（12）：2948-2952.

[11]叶蕾，郭海燕，杨震.基于压缩感知重构信号的说话人识别系统抗噪方法研究[J].信号处理，2010，26（3）：321-326.

[12]Xu T T，Yang Z，Shao X.Novel speech secure communication system based on information hiding and compressed sensing[C]//2009 Fourth International Conference on Systems and Networks Communications（ICSNC 2009），Porto，Portugal，2009：201-206.

[13]孙林慧，杨震.基于压缩感知的分布式语音压缩与重构[J].信号处理，2010，26（6）：824-829.

[14]叶蕾，孙林慧，杨震.基于压缩感知观测序列倒谱距离的语音端点检测算法[J].信号处理，2011，27（1）：67-72.

[15]季云云，杨震.基于自相关观测的语音信号压缩感知[J].信号处理，2011，27（2）：207-214.

[16]高悦，王改梅，陈砚圃，等.基于差分变换的语音信号压缩感知[J].信号处理，2011，27（9）：1434-1439.

[17]周小星，王安娜，孙红英，等.基于压缩感知过程的语音增强[J].清华大学学报：自然科学版，2011，51（9）：1234-1238.

[18]Figueiredo M A T，Nowak R D，Wright S J.Gradient projection for sparse reconstruction：application to compressed sensing and other inverse problems[J].IEEE Journal of Selected Topics in Signal Processing，2007，1（4）：586-597.

[19]Wright S J，Nowak R D，Figueiredo M A T.Sparse reconstruction by separable approximation[J].IEEE Transactions on Signal Processing，2009，57（7）：2479-2493.

[20]Donoho D L.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory，1995，41（3）.

[21]Grippo L，Sciandrone M.Nonmonotone globalization techniques for the Barzilai-Borwein method[J].Computational Optimization and Applications，2002，32：143-169.

[22]Noizeus：a noisy speech corpus for evaluation of speech enhancementalgorithms[EB/OL].[2013-07-03].http：//www. utdallas.edu/～loizou/speech/noizeus/.

[23]Spib noise data[EB/OL].[2013-07-03].http：//spib.rice.edu/ spib/select_noise.html.

[24]Ma J，Hu Y，Loizou P.Objective measures for predicting speech intelligibility in noisy conditions based on new band-importance functions[J].Journal of the Acoustical Society of America，2009，125（5）：3387-3405.

[25]Hu Y，Loizou P.Evaluation of objective quality measures for speech enhancement[J].IEEE Transactions on Speech and Audio Processing，2008，16（1）：229-238.

[26]ITU-T（2000）.Perceptual Evaluation of Speech Quality（PESQ）：an objective method for end-to-end speech quality assessment of narrowband telephone networks and speech codecs，ITU-T Recommendation P.862[EB/OL].[2013-07-03]. http：//www.itu.int/rec/T-REC-P.862/en.

[27]Loizou P，Ma J F.Extending the articulation index to account for non-linear distortions introduced by noisesuppression algorithms[J].The Journal of the Acoustical Society of America，2011，130（2）：986-995.

NING Kuangfeng,WANG Jingfang

School of Information Science and Engineering,Hunan International Economics University,Changsha 410205,China

Compressed Sensing（CS）which is a signal sparsity-based sampling method,can effectively extract the information contained in the signal.A new method is designed for noisy speech enhancement based on the grouping separation of compressed sensing.Speech sparse expression is used in discrete Fast Fourier Transform（FFT）domain.The algorithm can implement compression measurement and denoising in noisy speech by the design of the complex domain observation matrix and soft threshold.Sparse Reconstruction by Separable Approximation,SpaRSA algorithm is used to restore the speech signal,to achieve speech enhancement.The experiments show that the denoising signal can be compressed and reconstructed for noise signal compression refactoring.The signal-to-noise ratio can be improved greatly.The background noise can be more effectively suppressed.

speech enhancement;compressed sensing;group-separable;soft threshold;denoising

压缩感知（Compressive Sensing，CS）是一种基于信号稀疏性的采样方法，可以有效提取信号中所包含的信息。提出了一种分组分离压缩感知语音增强新算法。算法利用语音在离散快速傅里叶变换（Fast Fourier Transform，FFT）域下的稀疏性，设计复域观测矩阵与软阈值对带噪语音进行压缩测量与去噪，通过可分组分离逼近稀疏重建（Sparse Reconstruction by Separable Approximation，SpaRSA）算法恢复语音信号，实现语音增强。实验表明：该算法对含噪信号压缩重构，信噪比幅度较大提高，能更有效地抑制背景噪声。

语音增强；压缩感知；分组分离；软阈值；去噪

A

TN912.35

10.3778/j.issn.1002-8331.1309-0040

NING Kuangfeng,WANG Jingfang.Speech enhancement based on group-separable compressed sensing.Computer Engineering and Applications,2014,50（24）：204-208.

宁矿凤（1980—），女，讲师，主要研究领域为多媒体技术及应用，语音识别。E-mail：ning_candy@sina.com

2013-09-04

2014-01-20

1002-8331（2014）24-0204-05

CNKI网络优先出版：2014-07-11，http∶//www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1309-0040.html