模糊综合评判在矿山边坡稳定性评价中的应用

吕琨，李昌存，韩秀丽，陶志刚

（1.河北联合大学，河北 唐山063009；2.深部岩土力学与地下工程国家重点实验室，北京100083；3.北京矿冶研究总院，北京100160）

0 引 言

由于露天矿边坡是一个动态的开放系统，边坡岩体的力学特性参数、结构面分布规律都极其复杂多变。影响边坡稳定的因素很多，且因素与因素之间的关系复杂，往往呈非线性，很难用明确的数学方法或力学方法进行精确的描述和求解。通过一些新的学科和理论的引入与交叉，逐步形成了一些新的边坡稳定性分析方法。针对这一特点，许多学者提出了可靠度评价方法［1］、神经网络评价方法［2］、拉临沂格朗日元法、数值流形方法与无单元法、灰色系统理论［3－5］、模糊数学方法［6］等等。这些评价方法在边坡稳定性分析与评价中均取得了比较好的应用成果，推动了边坡稳定性研究的发展。

模糊综合评价方法将模糊数学理论运用到边坡稳定性分析与评价中，在处理边坡稳定性分析中的模糊性时具有一定的优势，首先找出边坡稳定性的影响因素，并进行分类，分别赋予一定的权值；然后，用隶属函数代替确定论中非此即彼的特征函数来描述其中具有模糊性的影响因素；最后，根据最大隶属度原则判断边坡单元的稳定性。

1 露天矿边坡稳定性主要影响因素

边坡岩体的稳定性受多重因素的影响，可分为内在因素和外在因素。内在因素主要包括边坡岩体的地层、组成边坡岩体的岩性、地质构造、岩土体结构、地应力以及水的作用等；外部因素主要指边坡形态的改造、气象变化、振动作用、工程荷载、植被作用以及人为因素的影响等。根据大量的野外地质调查和试验研究，把其影响因素分为五类：

（1）地形地貌条件：地貌条件决定了边坡形态，对边坡稳定性有直接影响。边坡的形态系指边坡的高度、坡角、剖面形态、平面形态以及边坡的临空条件等。对于均质岩坡，其坡度越陡，坡高越大则稳定性越差。对边坡的临空条件来讲，工程地质条件相类似的情况下，平面呈凹形的边坡较呈凸形的边坡稳定。

（2）岩性特征：边坡的滑落主要是剪切破坏，因此，岩体的抗剪强度是衡量边坡岩体稳定性的必要条件。

（3）岩体结构与地质构造：岩体中的断层、节理、层理和片理是边坡稳定性的控制因素。一般情况下，同向倾斜边坡比反向倾斜边坡稳定性差，同向缓倾边坡中，结构面倾角越陡，稳定性越差。结构面走向和边坡坡面走向之间的关系，决定了可能失稳边坡运动的自由程度，当倾向不利的结构面走向和坡面平行时，整个坡面都具有临空自由滑动的条件，因此对边坡的稳定最为不利；结构面走向与坡面走向夹角越大，对边坡的稳定越有利，而结构面充填的软弱物质会降低边坡抗剪强度，不利于边坡稳定。

（4）水的作用：水作为自然界极其常见的流体，在岩石中的作用与岩石的结构特征有很大关系，主要表现在两个方面：一是水的物理化学作用，其往往改变岩石的物质成分或结构；二是水的力学效应，这两种作用往往相互耦合，对岩石的受力过程产生影响，地下水富集程度的提高一方面增大坡体下滑力；另一方面降低软弱夹层和结构面的抗剪强度，引起孔隙水压力的上升，降低滑动下面的有效正应力，导致滑动面抗滑力减小。

（5）风化作用：岩石的风化速度、深度和厚度应取决于一系列的因素，如岩石的性质，断裂的发育程度，水文地质形态，水文、气象，地形地貌及现代物理地质作用等。在同一地区由于岩石性质不同，风化程度也不同。如粘土质页岩比硬砂岩易风化，风化较深，风化层的厚度也较大，边坡角较小，根据某些地区自然边坡实际调查资料，粘土质岩组成的边坡角均缓于36°，而砂岩边坡则较陡。

2 模糊数学综合评判基本原理

2.1 模糊数学综合评判三要素

（1）因素集：U＝｛u1，u2，…um｝，设与被评判对象相关的因素有 m个；

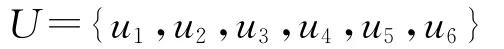
其中：

u1，u2…um分别为：坡脚，坡高，降雨强度，滑体特征综合影响指数，地质构造影响程度，矿山开采影响指数；

m为评价因子数，此处m＝6。

（2）评语集：V＝｛v1，v2，…vn｝，设所有可能出现的评语有n个；

在这里确定南芬露天铁矿稳定性，把危险性分为四个等级，即：式中n为评价等级数，此处n＝4。

（3）单因素判断，即对单个因素ui（i＝1，…m）的评判，得到V上的F集（ri1，ri2，…rin），所以它是从U到V的一个F映射。

如果着眼于第i（i＝1，2，…，n）个评判因素ui，其单因素评判结果为：

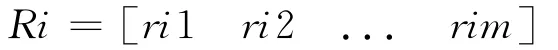
则各个评判因素的评判决策矩阵：

这就定义了U到V上的一个模糊关系。

如果各评判因素的权重分配为：

显然，A是论域U上的一个模糊子集，且，则通过模糊变换，可以得到V上的一个模糊子集，即综合评判结果

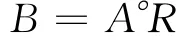
式中：B——所求的综合评价结果；

A——参与评价因子的权重归一化处理后构成的一个1×n阶矩阵；

R——由各单因子评价行矩阵组成的n×m阶模糊关系矩阵；

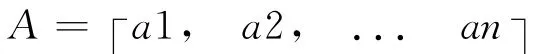
·——矩阵合成运算符号，其方法通常有两种：第一种是主因素决定模型法，即利用逻辑算子进行取小或取大合成，该方法一般适合于单项最优的选择；第二种是普通矩阵模型法，即利用普通矩阵乘法进行运算，这种方法兼顾了各方面的因素，因此适宜于多因素的排序。

2.2 模糊数学综合评价的过程与步骤

首先，选取待评价的边坡范围，划分出评价单元，然后选取评价因子，也就是影响边坡稳定行的因素，筛选出其中影响较大的若干因子，从定性分析的角度确定各因子的隶属度，从定量分析的角度确定各因子的隶属函数，最后确定评价因子的权重，进行归一化处理。

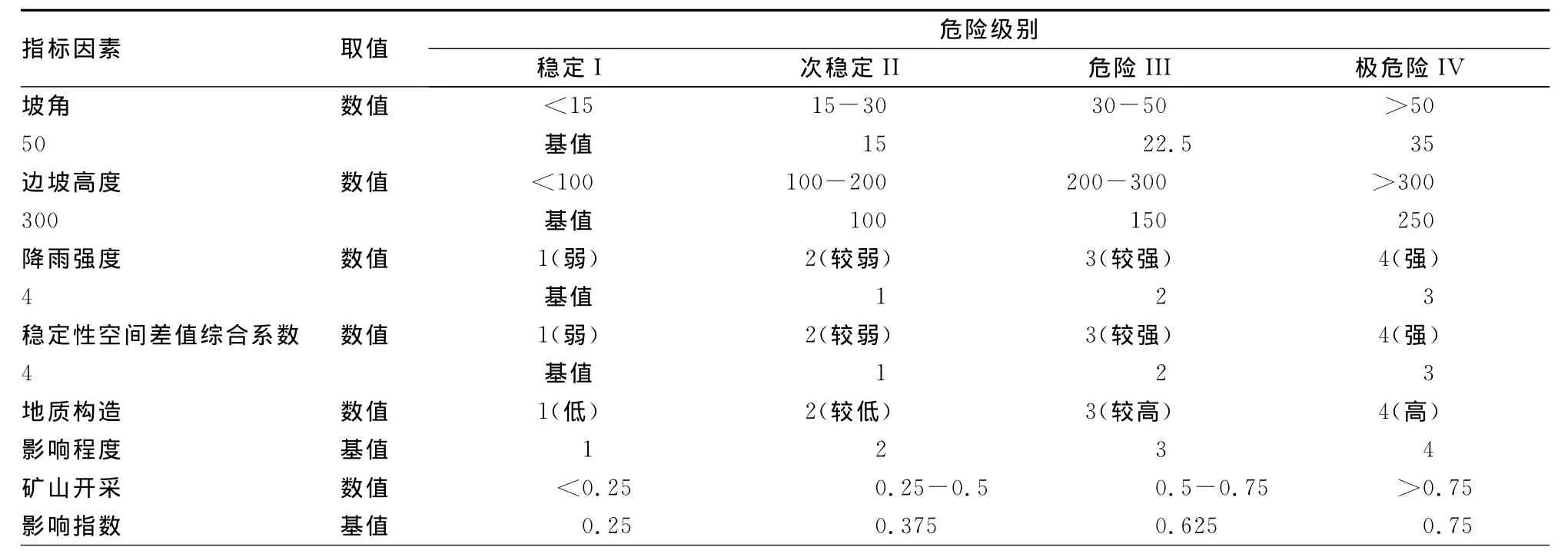
表1 影响因素级别划分［7］

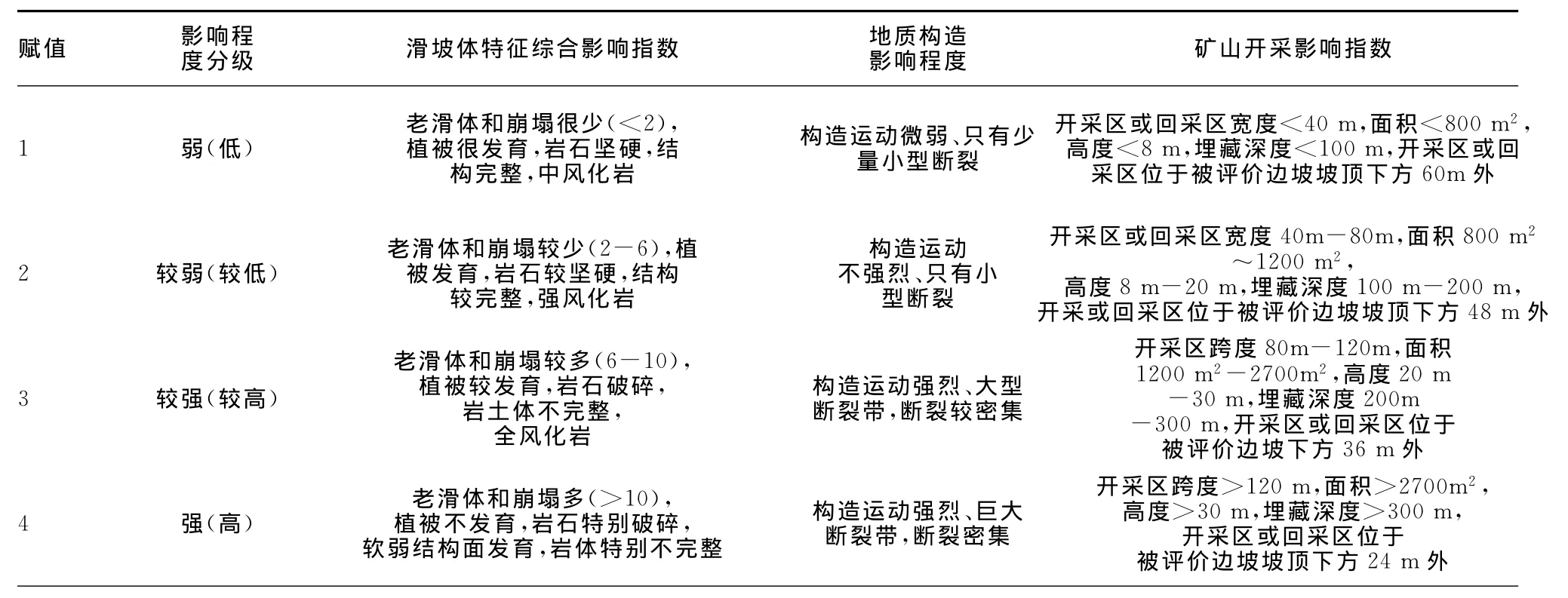
表2 离散型变量取值标准

综合以上数据，对边坡进行模糊运算，分析评价结果，若结果合理，即可确定各评价单元边坡危险性的等级，若结果不合理，再重新确定评价因子的权重。

由表1和表2可得边坡危险性综合评价分级标准集合：

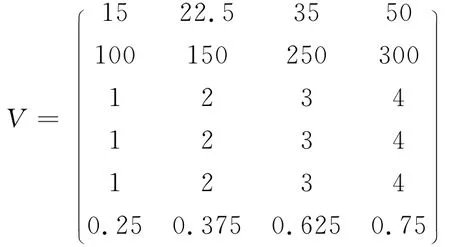
2.3 评价指标及隶属函数的确定

各评价因子相对于这四个危险等级的隶属函数可以按照梯型分布和三角分布（如图1）来计算，计算公式为：

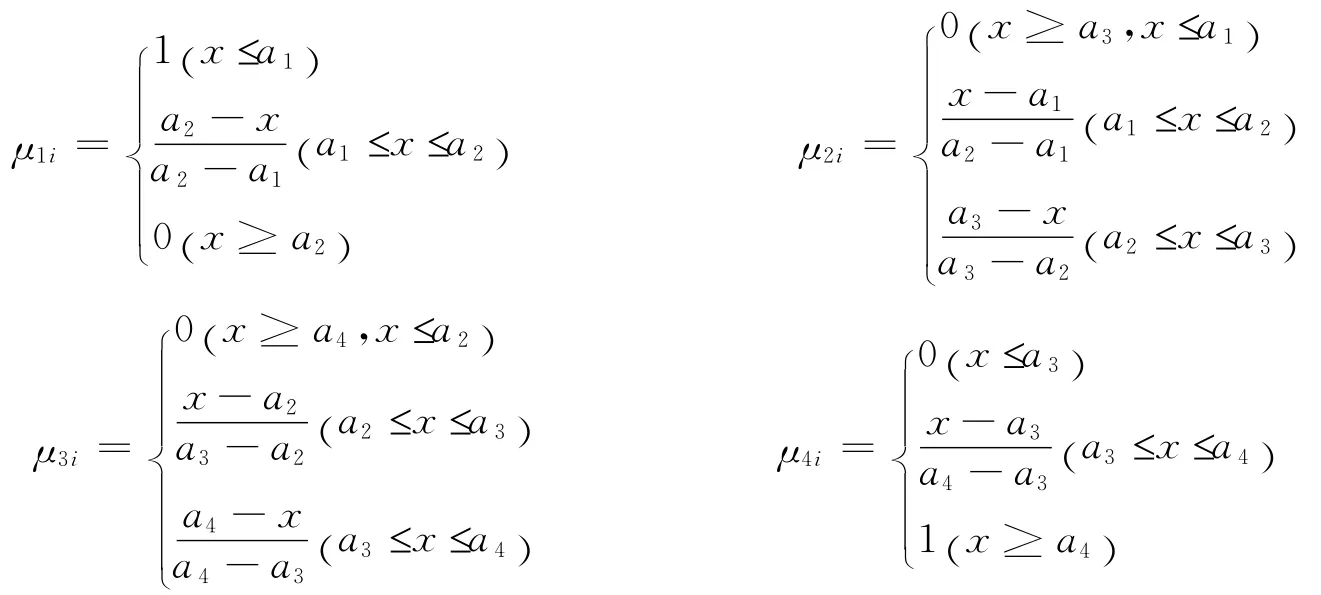
式中：

x——被评组的实测值；

ai（i＝1，2，3，4） ——I，II，III，IV级评价标准值。

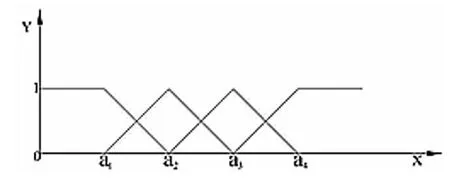
图1 梯形和三角形分布

2.4 权重的确定

应用模糊数学进行评判，隶属函数是一个关键，用它来反映边坡稳定性的稳定程度。

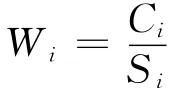
式中：

Ci——各种指标实测值；

Si——各指标等级代表值。

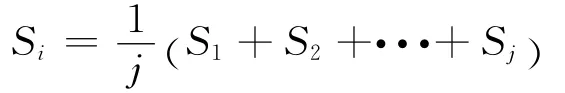
（注意：如果某项指标与其他指标相反，其值越大说明对边坡稳定性影响越小，这种情况权重计算要取倒数）

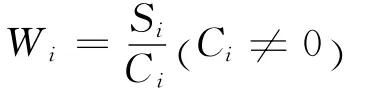
为了进行模糊运算，各单项权重值还必须归一化：

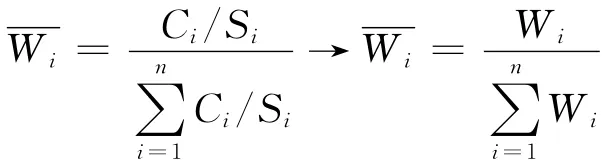
表3 权重计算表

3 工程实例

3.1 工程概况

南芬露天矿是亚洲最大的单体露天矿山。露天矿采场南北长3800m，东西宽1800m，比高达667m，属于高陡边坡类型。矿区采场经过多年开采，原始地形发生了翻天覆地的变化，采场中部和南部采掘垂深已经达到504m，采场底部标高190m，采场顶部（下盘）标高694m。北端也进行了大规模的开采，其中采场底部标高286m，采场顶部标高454m，采掘深度达到168m。

3.2 边坡危险性模糊综合评价

确定了隶属函数，便可以据此计算出6项因子各自对于模糊集合｛V1，V2，V3，V4｝4个危险等级的4个模糊隶属度，根据这4个隶属度，便可以形成由隶属度构成的一个（6×4）阶模糊关系矩阵。例如，任意选取某一个单元，其6个因子得分分别为（40、200、3、3、3、0.3），将每个数分别代入以上述隶属函数进行计算，便可得到一个（6×4）阶矩阵，如下：

上式中，每一行代表每一因子对于四个边坡危险性分区的隶属度。

将模糊关系矩阵R和权重分配矩阵A代入式B＝A·R中，即可得出该单元待评区的模糊综合评价结果。进行归一化处理得出：

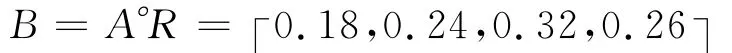
评价结果按最大隶属度决定，即哪一级的隶属度最大，则边坡危险等级就定哪一级。依照上述原则，由上式计算可知，该待评区属于III级，南芬露天铁矿边坡危险性较不稳定。

4 结 论

边坡的稳定性分析属于系统综合作用问题，各个影响因素既相互联系又随条件变化而变化，属于不确定性问题。通过对各个影响因素的综合分析，建立综合评判模型，据此对边坡稳定性作出模糊综合评判。通过实例分析结果表明，此方法简单快捷，分析结果可靠。对边坡稳定性进行分析预测具有指导意义。由于实际影响边坡稳定性的因素本身具有模糊性，因此该方法可作为传统分析边坡稳定性方法的一种补充，并作为工程设计的参考。

［1］ 孙玉科，杨志法.中国露天矿边坡稳定性研究［M］.北京：中国科学技术出版社，1999.

［2］ 王志忠.大孤山露天铁矿高陡边坡稳定性分析［D］.阜新：辽宁工程技术大学，2011.

［3］ 侯永莉.露天矿边坡稳定性分析方法综述［J］.科技创新导报，2009（12）：66－67.

［4］ 李金华.露天矿边坡稳定性的模糊综合评判［J］.西部探矿工程，2005（6）：213－214.

［5］ 沈良峰.岩土边坡稳定性分析的模糊综合评判实用方法［J］.湘潭矿业学院学报，2002，9（3）：72.

［6］ 马德元.边坡稳定性的模糊综合评判［J］.工程勘察，2002（6）：36.

［7］ 陶志刚，孙忠强，郭占飞，等.耦合多种成灾因素下的边坡稳定性分析［J］.地下空间与工程学报，2011，7（3）：293－603.