杭州市资本回报率的变动及其影响因素分析
——基于人力资本的视角
,
(浙江理工大学, a. 经济管理学院; b. 人事处, 杭州 310018)
资本回报率的高低在很大程度上引导了资本的流向,进而影响到地区的经济发展。积极探索资本回报率的提升路径是杭州扩大有效投资的重要思路之一,也是杭州加快转变经济发展方式,推动经济持续较快发展的战略选择。而如何从人力资本的视角揭示资本回报率的变动机制,改变传统的投资驱动型经济增长方式,是杭州经济突破资本约束、实现科教人才强市战略的关键手段。
Schultz[1]较早地对人力资本进行过研究,后经Becker等[2]的进一步研究和完善,进而形成了人力资本理论。人力资本还会产生溢出效应,进而影响到资本的回报率。国内外学者研究的代表性观点有以下三点:一是认为人力资本通过吸引先进资本和技术,进而影响到资本回报率的变动。如Lucas[3]和沈坤荣等[4]的研究都支持这一观点;二是认为人力资本存量的变动会导致资本劳动比率的变动,进而提高或降低资本的回报率。如Romer[5]、张军[6]和孙文凯等[7]的研究都有着类似看法;三是认为因人力资本存量变动导致的资本深化并不必然导致资本回报率的变化。如Gordon[8]和黄伟力[9]认为,资本深化对资本回报率的负向影响并不一定存在,两者之间存在着复杂的关系。
从以往文献来看,现有研究至少还存在以下几方面的不足:一是现有研究多是基于国家层面对中国资本回报率进行分析,但国家层面的研究结论很难应用在杭州市级层面;二是对资本回报率变动机制的分析上,还未出现相应的理论模型,更没有形成统一的理论分析框架;三是现有文献多是从“劳动力数量”的视角进行研究,忽略了“人力资本及其溢出效应”对资本回报率的重要影响。针对上述不足,本文修正并完善了Lucas的人力资本模型,区分了人力资本的不同类型,进而得到分析资本回报率变动机制的理论分析框架,并以理论分析框架为基础建立计量模型,对杭州规模以上工业数据进行了动态的分析,以期为企业和政府决策提供理论依据。
一、理论模型
本文借鉴Lucas的研究模型,并将劳动者区分为无技术水平工人和人力资本(技术工人),并认为人力资本存在溢出效应,进而构建经济总的生产函数为:
Y=A(t)K(t)β[u(t)h(t)N(t)]αha(t)γl(t)η
(1)
对式(1)求导可得资本的回报率为:
r=MPK=βA(t)K(t)β-1
[u(t)h(t)N(t)]αha(t)γl(t)η
(2)
其中,Y为总产出,A(t)表示技术水平,K(t)表示资本存量,N(t)表示劳动者数量,0<α<1,0<β<1。假定人力资本为h(t)的劳动者总量为N(h),工人将总生产时间的u(t)部分用于物质生产,剩余部分(1-u(t))生产人力资本(如劳动者自身技能的提高),则经济中全部的人力资本为u(t)h(t)N(t),为人力资本的溢出效用,本文假定ha=h。l(t)表示无技术水平工人的数量。
同时假定消费的效用函数为:
[N(t)+l(t)]dt
(3)
其中,c(t)为人均消费,ρ表示贴现率,σ表示相对风险规避系数,ρ>0,σ>0。
假设所有产品均被用来消费和资本积累,根据最优消费理论,并借鉴Uzawa[10]和Rosen[11]关于人力资本的积累模型,可以推导出经济的均衡:
(4)
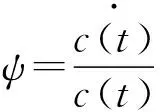
二、资本回报率的计算
根据Bai等[12]的研究,资本回报率的计算模型如(5)式所示:
(5)
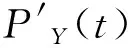
数据主要来源于历年《杭州市统计年鉴》。为了使时间序列趋势线性化,消除异方差现象,在下文的计量分析部分对原数据进行了自然对数处理。物质资本存量:本文使用企业的固定资产总计作为代理变量;人力资本存量:衡量了劳动者知识和技术的积累程度,本文使用企业技术人员数量作为人力资本存量的代理变量。人力资本的溢出效应:根据Lucas的研究,经济中所有劳动者平均的人力资本水平可以作为人力资本溢出效应的代理变量,因此本文使用工业企业技术人员数量占总的劳动工人的比例作为溢出效应的代理变量;无技术水平工人:使用总的劳动工人数量减去技术人员的数量作为代理变量。
使用1990-2012年杭州市规模以上工业企业的数据,对其资本回报率进行计算,结果如图1所示。杭州规模以上工业企业资本回报率总体上呈U型,1995年资本回报率出现了较大幅度下降,到1996年降至最低水平,位于15%以下,然后开始逐渐回升。这主要是因为20世纪90年代初期,改革开放加剧了市场的竞争程度,因此工业企业的资本开放加剧了市场的竞争程度,因此工业企业的资本回报率出现了大幅回落。进入21世纪之后,企业的资本回报率已增长至较高水平,基本在25%~30%之间,但在美国次贷危机的影响下,2008年和2009年的资本回报率略有下降。根据理论分析可知,人力资本等因素对资本回报率有着重要影响,因此下文将使用杭州市的具体数据进行实证分析。

图1 杭州规模以上工业企业资本回报率
三、实证检验
(一)单位根检验
在表1中,r表示资本回报率,k表示资本存量,H表示人力资本,ha表示人力资本的溢出效应,l表示无技术水平工人,ln表示对变量取自然对数,ΔΔ表示变量的二阶差分,数据具体说明及来源同资本回报率的计算部分。首先对各个变量进行单位根检验,以确定各单位序列是否满足协整分析所需的同阶单整的要求。ADF检验方法是较为常用的方法之一,因此本文采用该方法进行单位根检验,所使用软件为Eviews6,检验结果如表1所示。原数据的检验结果均是不平稳的,一阶差分后仍是不平稳,但二阶差分后则不再存在单位根,符合进行协整分析所需的同阶单整的条件。
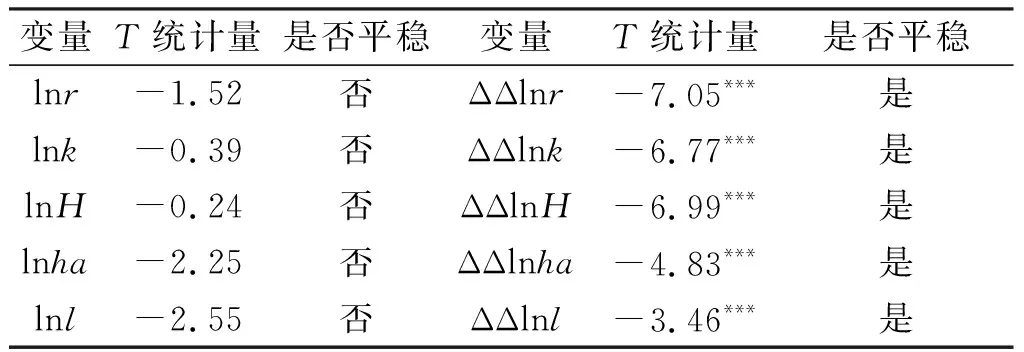
表1 ADF单位根检验结果
(二)滞后期选择
本文实证分析的变量有5个,每个变量均包含1990-2012年的数据,因此可以使用基于VAR模型的Johansen极大似然检验法进行协整检验。VAR模型滞后期的选择可以根据下列信息进行判定:一个统计量(LR)和四个准则(FPE、AIC、SC、HQ),相关的结果见表2。由表2检验结果可知,所有指标均显示选择滞后2期的VAR模型是最优的。

表2 滞后期检验结果
注:*表示该标准所选择的滞后阶数。
为了确保所建立的二阶滞后模型是准确的和稳定的,需进一步进行自相关检验。检验结果表明,LM(2)的值为31.07,概率P等于0.19,因此可以拒绝残差序列存在自相关的假设;AR根的检验显示VAR(2)模型所有根的模的倒数均位于单位圆之内,因此本文建立的VAR(2)模型是稳定的(如图2所示)。
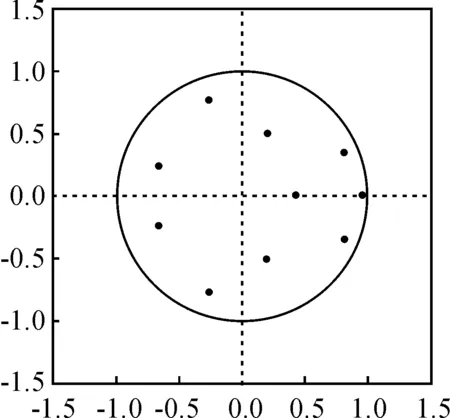
图2 AR根的检验
(三)Johansen协整检验
根据上述检验结果,选择二阶滞后期,建立VAR(2)模型进行Johansen检验。迹统计量和最大特征值方法可以检验变量之间存在的协整关系个数,进而确定变量之间是否存在长期均衡关系,检验结果如表3和表4所示。
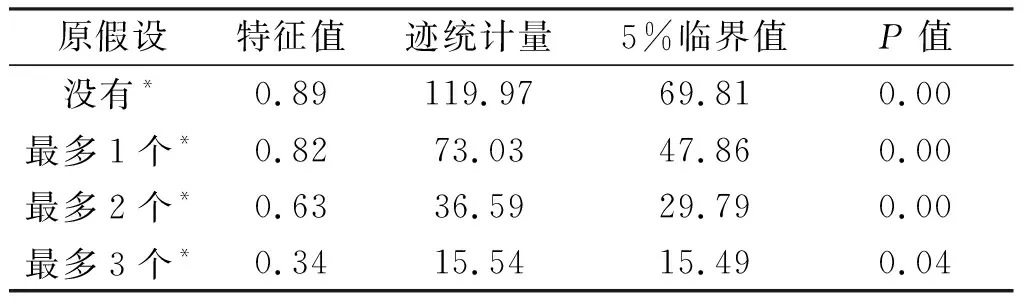
表3 迹统计量的检验结果
注:*表示拒绝原假设。
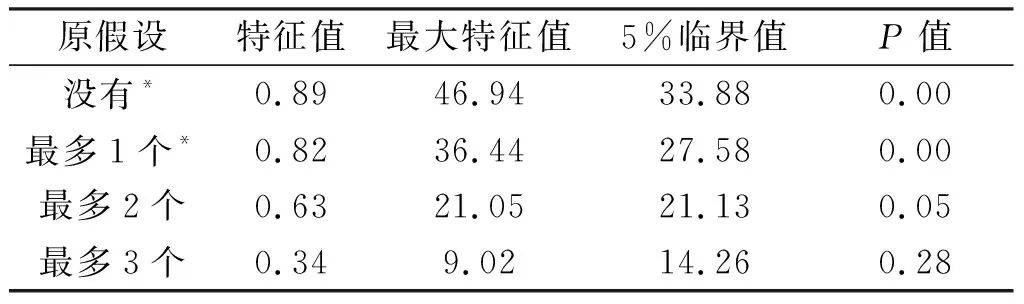
表4 最大特征值的检验结果
注:*表示拒绝原假设。
迹统计量和最大特征值检验结果均表明五个变量之间存在着长期均衡关系,因此可以对变量之间的协整关系进行分析。杭州市资本回报率与其影响因素之间的标准化系数如表5所示,该标准化系数显示了各因素对杭州资本回报率的长期影响。由表5可知,杭州人力资本在长期对资本回报率有着显著的促进作用,人力资本每提高1%,资本回报率提升5.46%;同时,人力资本溢出效应的存在却导致了资本回报率的下降,溢出效应增加1%,资本回报率下降7.23%,影响较为明显;无技术水平工人的增加会降低杭州的资本回报率,无技术水平工人增长1%,资本回报率下降5.78%;资本存量的增长在长期能够提高杭州的资本回报率,资本存量每增加1%,资本回报率增长0.53%,由此可见,资本存量对资本回报率的促进作用要小于人力资本的促进作用。

表5 标准化协整系数
注:括号内表示标准误差。
(四)向量误差修正模型
上文对变量间的长期均衡关系进行了分析,为了进一步分析人力资本等因素的短期变动对资本回报率的影响,可以使用上述标准化协整系数分析的残差序列与各变量的一阶差分序列构建向量误差修正模型(VEC),进而观察变量之间的短期动态关系。下式为计量分析结果:
d(lnr)=-0.69[lnr(-1)-5.78lnl(-1)+
0.53lnk(-1)-7.23lnha(-1)+5.46lnh
(-1)-5.57]-0.42lnd(r(-1))-5.28d
(lnl(-1))-1.05d(lnk(-1))-6.63d
(lnha(-1))+5.59d(lnH(-1))+0.18
(6)
由式(6)可知,人力资本短期调整系数为正,其他三个影响因素的短期调整系数均为负。因此认为人力资本的提升在短期也可以促进资本回报率的提升,这与其长期影响是相同的,人力资本的溢出效应和无技术水平工人在短期对资本回报率也有着负向影响,而资本存量在短期的影响却与长期影响有着相反的效果,短期来看,资本存量的增长降低了杭州的资本回报率。
(五)脉冲响应
脉冲响应可以更加清晰地反应各影响因素与资本回报率之间的长短期关系,因此本文在VEC模型的基础上,使用脉冲响应函数分析了各影响因素受到冲击时对资本回报率的动态影响,具体的分析结果如图3-图6所示,其中横轴表示冲击的时间,纵轴表示各冲击对r的累积效应,中间实线表示r对各种冲击的影响,上下两条虚线表示正负两倍标准差的偏离带。
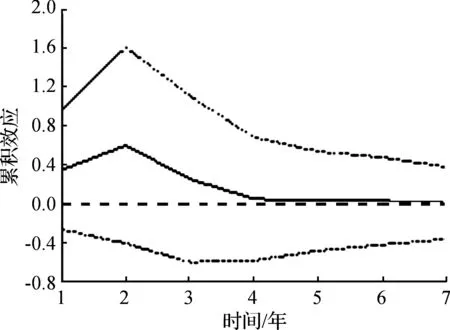
图3 r对H冲击的响应
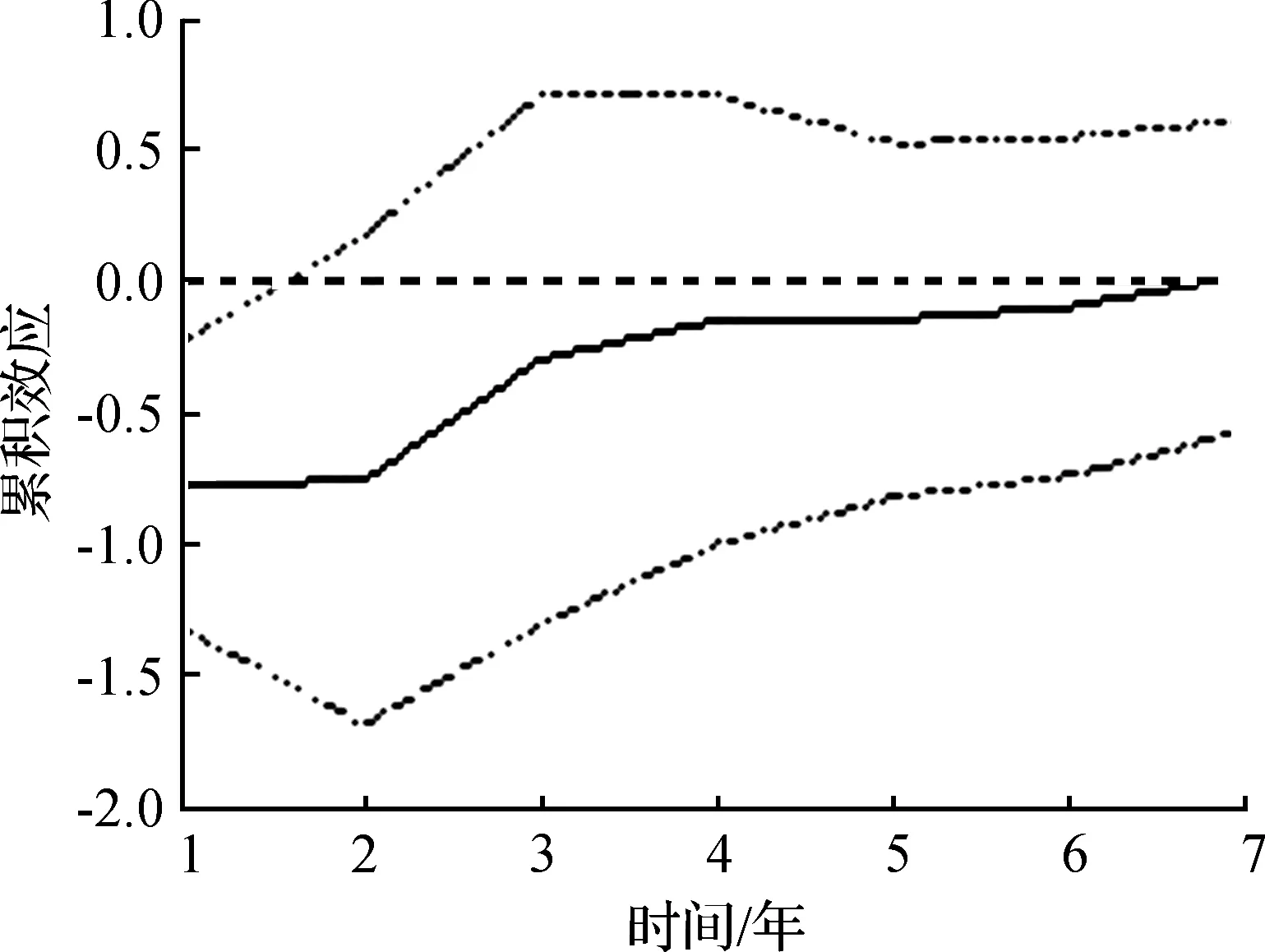
图4 r对ha冲击的响应
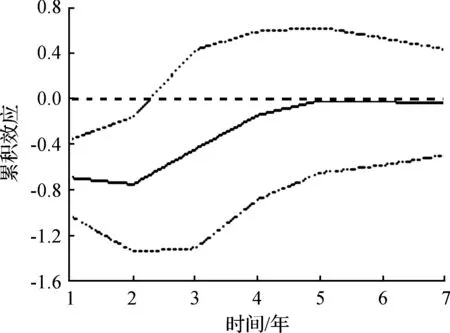
图5 r对l冲击的响应
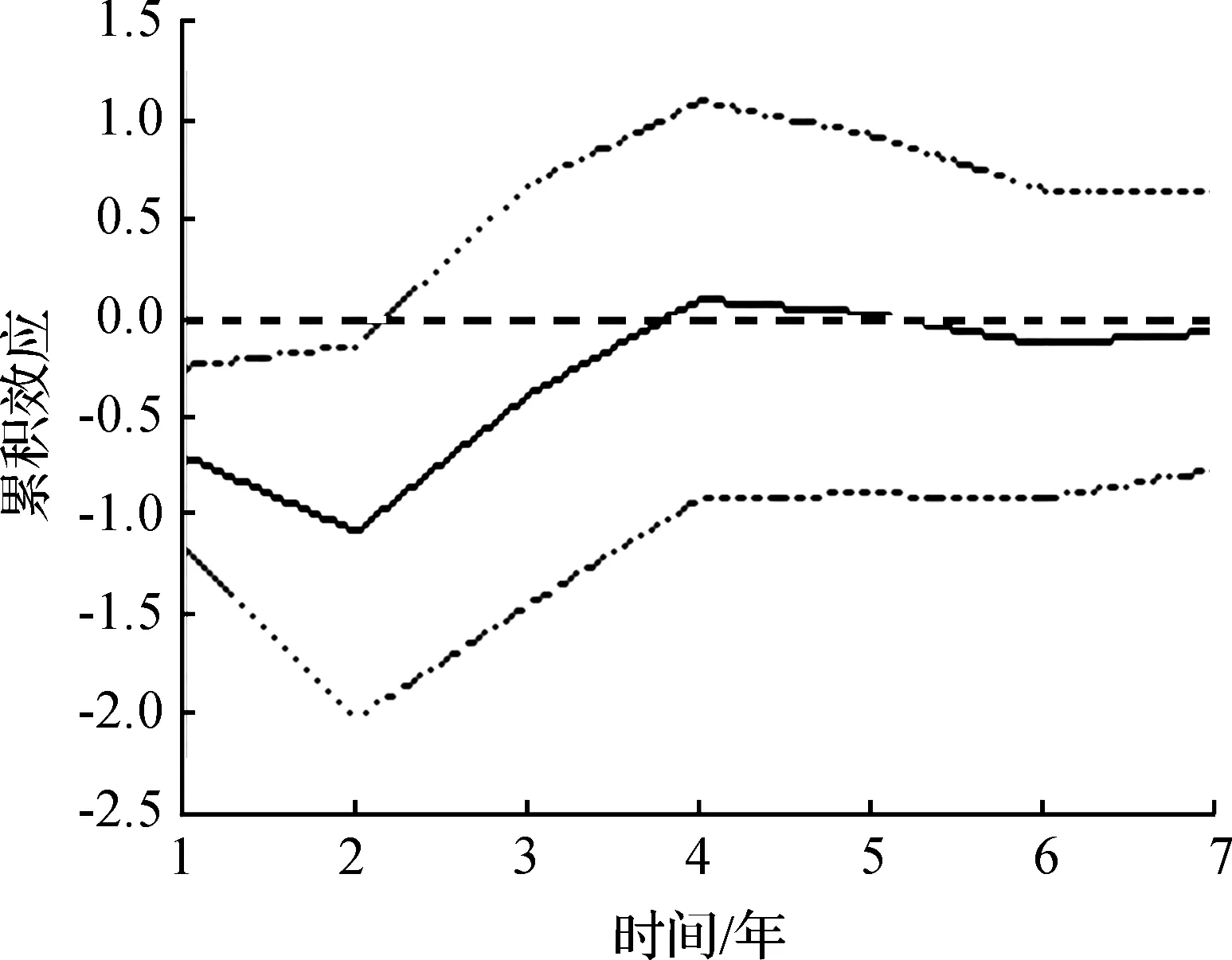
图6 r对k冲击的响应
a) 在本期给人力资本(H)一个正的冲击,资本回报率(r)在第二期会上升到最高点,随后人力资本冲击的效应会逐渐下降并最终趋向于零(如图3所示)。这说明工人的人力资本水平在短期和长期对资本回报率都有着较为显著的促进作用,但这种促进作用最终会随着时期的增加而消失。较高的人力资本水平意味着较高的生产效率,进而增加资本的产出并提高资本的回报率,且这种促进作用能够持续一段较长的时期。但由于知识更新速度越来越快,人力资本的促进作用也不可能无期限的持续下去,因此在一个更为长期的时间范围内,对人力资本的投资并不是一劳永逸的,而应是一个持续的过程。即企业应不断进行人力资本的投入,提高工人的技术水平和生产效率,从而保持资本回报率的稳定增长。
b) 在本期给人力资本溢出效应(ha)一个正向冲击,资本回报率(r)会出现剧烈下降,且持续一个较长的时间,但资本回报率下降的幅度随着时期的增加而不断减弱,最终趋向于零(如图4所示)。人力资本溢出效应的提高会降低资本回报率,且这种降低作用会持续一个较长时期。人力资本外溢效应的出现,会导致企业技术知识的损失,从而降低企业的资本回报率。从长期来看,这种溢出效应使得企业无法获取人力资本投入的全部回报,因此不愿意持续进行人力资本投入,资本回报率也因人力资本的下降而下降。溢出效应属于市场无法解决的一种外部性,因此政府应该进行适当的宏观调整,出台相应政策使这种溢出效应内部化,增加企业投资人力资本的积极性,从而降低人力资本溢出效应的不利影响,促进经济的健康发展。
c) 在本期给无技术水平工人(l)一个正向冲击,资本回报率(r)会出现剧烈下降,在第五期之后,冲击的效应逐步趋向于零(如图5所示)。这与人力资本溢出效应的结果比较类似,即无技术水平工人数量的增长在短期和长期都会导致资本回报率的下降。无技术水平工人的增加会提高企业的人力成本,而无技术水平工人由于知识和技能的缺乏,对企业生产效率提高的影响较弱,在回报增加小于人力成本上升的情况下,企业的资本回报率便会出现下降,且该影响会持续一个较长的时期。这也在一定程度上说明,随着杭州总体工资水平的增长,无技术水平工人使用成本的不断上升已导致了企业资本回报率的下降,因此相关企业,特别是劳动密集型企业,应改变低端发展之路,加大工人的知识和技能投入,实现投资质量和效益的提升。
d) 在本期给资本存量(k)一个正向冲击,资本回报率(r)会出现较大幅度的下降,随后下降幅度会逐渐减小,在第4期出现了一个较小的增长情况,随后逐渐趋向于零(如图6所示)。这与上文分析结论一致,即在一个较短的时期内,资本存量的增加会导致投资成本的大幅提高,进而降低资本的回报率,在长期,资本存量对资本回报率有着促进作用,但程度较低。政府主导的投资驱动增长模式使得资本深化程度较高,但杭州发展所缺的并不是资本,单靠投资已无法保证经济的持续增长。且企业的投资会使当期成本急剧增长,进而在短期出现资本回报率的快速下降,在长期虽有可能因此规模扩大带来资本回报率的提升,但效果可能并不明显。
四、结论与启示
本文首先从理论上分析了人力资本及其溢出效应对资本回报率的影响,然后使用杭州工业企业的数据进行了实证检验,具体的结论与启示有:
a) 杭州规模以上工业企业的资本回报整体上呈U型。20世纪90年代初期,中国市场化改革加速,竞争加剧,杭州市规模以上工业资本回报率开始出现较大幅度下降,进入21世纪之后,资本回报率已增长至较高水平,基本处在25%~30%之间。
b) 人力资本在长期和短期均促进了资本回报率的提升。人力资本的提升可以显著提高杭州的资本回报率,因此大力进行人力资本投资,提高工人的技术水平和生产效率,可以保持资本回报率的稳定增长。
c) 人力资本的溢出效应和无技术水平工人增长对资本回报率则有着负向作用。人力资本溢出效应的不利影响是企业自身是无法解决的,因此政府应出台相关政策鼓励企业进行人力资本投资。另一方面,仅仅增加企业工人的数量已无法提高资本的回报率,甚至出现负向影响,不利于经济的持续健康发展,因此企业在增加工人的同时,更应注重对人员技能的培训。
d) 资本存量在短期对资本回报率有着显著负的影响,长期则有着促进作用,但程度较弱。当前杭州经济发展已由资本短缺向资本高度深化转变,投资数量的增加已无法带来资本回报率的显著提高,因此企业应转变投资驱动型的增长模式,加大对人员、技术的投资,跨入集约化增长之路。
参考文献:
[1] Schultz T W. Capital formation by education[J]. The Journal of Political Economy, 1960, 68(6): 571.
[2] Becker G S, Chiswick B R. Education and the distribution of earnings[J]. American Economic Review, 1966, 56(1): 358-369.
[3] Lucas R. Why doesn’t capital flow from rich to poor countries?[J]. American Economic Review Papers and Proceedings, 1990, 80(2): 92-96.
[4] 沈坤荣, 田 源. 人力资本与外商直接投资的区位选择[J]. 管理世界, 2002(11): 26-31.
[5] Romer P M. Increasing returns and long-run growth[J]. Journal of Political Economy, 1986, 94(5): 1002-1037.
[6] 张 军. 资本形成、工业化与经济增长: 中国的转轨特征[J]. 经济研究, 2002(6): 3-13.
[7] 孙文凯, 肖 耿, 杨秀科. 资本回报率对投资率的影响: 中美日对比研究[J]. 世界经济, 2010, 382(6): 3-24.
[8] Gordon R J. Economic growth since 1870: what we know and still need to know[J]. American Economic Review, 1999, 89(2): 320-352.
[9] 黄伟力. 中国资本利润率的变动趋势及其影响因素[J]. 山西财经大学学报, 2007, 29(8): 15-21.
[10] Uzawa H. Optimum technical change in an aggregative model of economic growth[J]. International Economic Review, 1965, 6(1): 18-31.
[11] Rosen S. A theory of life earning[J]. The Journal of Political Economy, 1976, 84(8): 45-68.
[12] Bai C E, Hsieh C T, Qian Y Y. The return to capital in China[J]. Brookings Papers on Economic Activity, 2006, 19(2): 61-102.
[13] 单豪杰, 师 博. 中国工业部门的资本回报率: 1978-2006[J]. 产业经济研究, 2008, 37(6): 1-9.

