基于分布估计蜂群算法的多用户检测器

刘 婷，张立毅,2，张晋斌

(1.天津商业大学信息工程学院, 天津 300134；2.天津大学电子信息工程学院,天津 300072；3.宜昌测试技术研究所,湖北 宜昌 443003)

1 引言

多用户检测技术是降低多址干扰、克服远近效应的有效方法之一，是码分多址CDMA(Code Division Multiple Access)系统的关键技术。它在传统检测基础上，充分利用多址干扰的先验信息对目标用户进行联合检测，具有较理想的抗多址干扰和抗远近效应能力。Verdú S[1]提出的最优多用户检测技术具有理论上的最佳性能，但计算复杂度随用户数的增加呈指数增长，几乎无法实现。从组合优化的角度考虑，最优多用户检测属于非确定多项式NP(Non-Deterministic Polynomial)问题，经典优化算法对此类大规模复杂优化问题显得无能为力，因此人们往往采用智能优化算法进行求解，如基于鱼群算法的多用户检测器[2]、基于蚁群优化算法的多用户检测器[3]以及基于粒子群优化算法的多用户检测器[4，5]等。

人工蜂群算法ABC(Artificial Bee Colony)是Karaboga D[6]于2005年提出的一种模仿蜂群智能采蜜行为的新型智能优化算法，它通过角色间的转换使算法具有较强的全局和局部搜索能力，增加了找到最优解的概率且在很大程度上避免了早熟现象。由于其具有收敛速度较快、控制参数少、易于实现等优点[7]，被广泛应用于数字滤波器设计[8]、神经网络训练[9]和数据挖掘[10]等领域。标准ABC算法主要用于连续优化领域，为求解组合优化问题，Marinakis Y等[11]于2009年提出了一种称为BinABC的二进制人工蜂群算法。2012年，Liu Ting等[12]将BinABC算法用于求解多用户检测问题，提出了基于BinABC算法的多用户检测方案，但该方案存在收敛速度慢、易早熟等缺点。

分布估计算法EDA(Estimation of Distribution Algorithm)[13]是一种基于概率模型的智能优化算法，它从统计学习角度出发，依据概率模型描述整个群体的进化，利用种群的全局信息进行建模，具有良好的全局探索能力。本文将分布估计算法与人工蜂群算法相结合，提出一种基于分布估计的二进制人工蜂群算法，并应用于求解最优多用户检测问题。所提算法利用了人工蜂群算法具有较强搜索能力和有效避免局部最优的优势，结合分布估计算法可获得全局群体信息的特点，增强算法性能，更有效地求解最优多用户检测问题。仿真结果表明，所提多用户检测方案的收敛性能、误码率性能和抗远近效应性能均明显优于传统检测器。

2 多用户检测模型

考虑具有K个用户共享的同步基带CDMA信道，信号经高斯信道传输，接收端接收到的基带信号为：

(1)

其中，Ak为第k个用户的幅度；bk∈{-1,+1}为第k个用户的信息比特值；T为码元持续时间；sk(t)为第k个用户具有单位功率的特征波形；z(t)为具有单位功率谱密度的加性高斯白噪声AWGN(Additive White Gaussian Noise)；σ2为噪声的方差。

接收信号通过匹配滤波器组进行相干处理，第q个匹配滤波器的输出yq为:

(2)

y=RAb+z

(3)

(4)

最优多用户检测器采用Bayes后验概率最大原理，其目的是在解空间寻找字符矢量b使得以下函数最大化:

J(b)=2bTAy-bTHb

(5)

其中，H=ARA。

3 人工蜂群算法

人工蜂群算法包括三种角色：引领蜂、跟随蜂和侦察蜂。它的基本原理为：引领蜂首先飞出蜂巢，在对应食物源周围进行邻域搜索并利用“贪婪原则”进行选择。回到蜂巢后，引领蜂将食物源信息通过跳摇摆舞的形式传递给跟随蜂，跟随蜂观察引领蜂的食物源信息，选择优秀食物源进行跟随，并再次在其附近进行邻域搜索和“贪婪选择”。当某个食物源被放弃，与之对应的引领蜂成为侦察蜂，开始寻找新食物源。

利用ABC算法求解最大化问题时，蜜蜂采蜜与函数优化间的对应关系如表1所示。

ABC算法的具体实现过程如下。

(1)初始化。

Table 1 Relationships between honeybee foraging and function optimization表1 蜜蜂采蜜与函数优化对应关系

设置最大循环次数MCN和引领蜂转换为侦察蜂的次数limit，随机生成SN个初始食物源(解)x=(x1,x2,…,xi,…,xSN)，计算每个食物源的食物浓度。Karaboga D等[14]认为，引领蜂的数量应与跟随蜂相同，都等于食物源数量；侦察蜂的数量为1。

第i个食物源表示为xi=(xi1,xi2,…,xiD)，其中D为问题维数，它由以下方式初始化:

xid=xid,min+(xid,max-xid,min)rand1

(6)

其中，d∈{1,2,…,D}，xid,max和xid,min分别是xid的上、下限；rand1为(0，1)之间的随机数。

利用式(7)计算第i个食物源的食物浓度(适应度值):

(7)

其中，f为对应优化问题的目标函数。

(2)引领蜂行为。

引领蜂首先在对应食物源上进行一次邻域搜索，并采用“贪婪”原则进行选择。对食物源xi进行邻域搜索，产生新食物源vi=(vi1,vi2,…,viD)的公式为:

(8)

其中，l为[1,SN]的随机整数且l≠i；drand为[1,D]的随机整数；rid∈[-1,1]是一个随机数，控制邻域搜索的范围。

(3)跟随蜂行为。

引领蜂完成搜索后，回到舞蹈区把食物源的信息传达给跟随蜂。跟随蜂根据“轮盘赌”方式选择食物源。食物浓度越高的引领蜂招募到的跟随蜂越多。第i个食物源被选中的概率为:

(9)

其中，Pi称为转移概率。

跟随蜂也在选中食物源附近进行邻域搜索和“贪婪”选择。若跟随蜂搜索新食物源的食物浓度大于原引领蜂的旧食物源时，替换原引领蜂的旧食物源，完成角色互换；反之，保持不变。

(4)侦察蜂行为。

为了增加种群多样性，防止算法陷入局部最优，当某食物源的食物浓度连续limit次没有被更新，应该被放弃，与之对应的引领蜂变为侦察蜂，并根据式(6)随机生成新食物源。

(5)结束。

判断是否满足算法结束条件，若满足，输出目前找到的最优食物源；若不满足，返回继续执行引领蜂、跟随蜂和侦察蜂行为。ABC算法的结束条件通常设为循环次数递减至零或满足允许的误差值。

上述标准ABC算法只适用于连续优化领域，而最优多用户检测属于二进制优化问题，需要采用二进制人工蜂群算法BABC(Binary Artificial Bee Colony)算法。

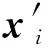
(10)

(11)

(12)

(13)

其中，rand2和rand3均为(0，1)的一个随机数。

BinABC算法的其他实现过程与标准ABC算法相同。

4 分布估计算法

分布估计算法是一种基于概率模型的进化算法，与传统进化算法不同，它不采用交叉、变异等操作，而是根据当前种群的概率分布产生下一代种群[17]。在分布估计算法中，先对个体进行统计分析，按照某种准则建立概率模型，然后采样产生下一代种群，如此反复直到找到最优解。

分布估计算法的实现步骤如下[18]：

(1)初始化种群；

(2)选择：根据适应度值选择优势群体；

(3)建模：根据优势群体，采用某种准则建立概率模型；

(4)抽样：根据概率模型，随机抽样产生新一代种群；

(5)判断是否满足结束条件，若满足，输出种群中的适应值最好的个体，若不满足，返回执行(2)。

分布估计算法包括多种概率模型，其中最简单且应用最广的是基于群体的增量学习PBIL(Population-Based Incremental Learning)算法，本文采用PBIL来建模。

5 基于分布估计二进制人工蜂群算法的多用户检测技术

5.1 基于分布估计的二进制人工蜂群算法

本文把分布估计算法思想引入二进制人工蜂群算法，提出一种基于分布估计的二进制人工蜂群算法EDBABC(Estimation of Distribution Binary Artificial Bee Colony)，并将其用于优化最优多用户检测问题。

EDBABC算法能把EDA获得的全局群体信息和BABC得到的局部个体信息相结合，提高算法性能。在EDBABC算法中，采用概率矢量P=(P1,P2,…,Pd,…,PD)表示优质解空间分布的概率模型，其中Pd(d=1,2,…,D)表示优质解空间第d维取1的概率，初始时刻Pd均为0.5。

EDBABC算法的具体实现过程如下。

(1)初始化。

(2)引领蜂行为。

引领蜂在对应食物源上进行一次邻域搜索，并采用“贪婪”原则进行选择。邻域搜索方式是整个EDBABC算法的核心，新的邻域搜索公式为：

(14)

(15)

其中，rand5为(0，1)的随机数。上式说明，概率矢量P引导着食物源的更新，因此EDBABC算法具有更好的全局特性。

(3)更新概率矢量。

按照以下方式更新概率矢量P：选择Z(Z=SN/2)个适应度值较高的优秀解组成优秀解空间{x′1,x′2,…,x′i,…,x′Z}，其中x′i=(x′i1,x′i2,…,x′id,…,x′iD)，根据PBIL模型构建概率矢量更新公式:

(16)

其中，α表示学习速率，0<α<1，它可以平衡算法全局探索能力和局部开采能力[18]。

(4)跟随蜂行为。

跟随蜂选择食物源后，仿照引领蜂，采用式(14)、式(15)进行邻域搜索、完成“贪婪”选择。

(5)更新概率矢量。

选择Z个优秀解，利用式(16)更新概率矢量。

(6)侦察蜂行为。

判断是否有需要放弃的解，如果有，引领蜂变成侦察蜂，为了增加种群多样性，仍采用随机生成的0、1代替旧解，找到新解后侦察蜂又变为引领蜂。

(7)结束。

5.2 基于分布估计二进制人工蜂群算法的多用户检测技术

把最优多用户检测搜索最佳字符矢量的过程看作是分布估计二进制人工蜂群算法寻找最优解的过程，可得到基于分布估计二进制人工蜂群算法的多用户检测(EDBABC-MUD)。

(17)

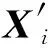
(18)

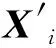
(19)

基于EDBABC算法的多用户检测的具体实现步骤为：

(1)初始化。

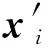
(2)执行循环。

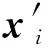
③ 更新概率矢量：选择Z个优秀解，利用式(16)更新概率矢量。

⑤ 依据转移概率，跟随蜂选择引领蜂进行跟随，并利用式(14)和式(15)进行邻域搜索，完成“贪婪”选择。

⑥ 更新概率矢量：选择Z个优秀解，利用式(16)更新概率矢量。

⑦ 判断是否有需要放弃的解。如果有，引领蜂变成侦察蜂，利用随机生成的0、1代替旧解。

⑧ 记录到目前为止的最优解。判断是否满足算法的终止条件。若满足，输出找到的最优解(注意，需要映射到-1、1空间)，否则继续循环。

6 计算机仿真

考虑高斯同步DS-CDMA通信系统，采用31位Gold序列来扩展频谱，选用以下检测器进行性能比较：基于EDBABC算法的多用户检测器(EDBABC-MUD)、基于BinABC算法的多用户检测器[12](BinABC-MUD)、基于PBIL的多用户检测器(PBIL-MUD)、解相关多用户检测器(Decorr)、匹配滤波器(Match)和最优多用户检测器(OMD)。

6.1 收敛性能

EDBABC-MUD、BinABC-MUD和PBIL-MUD的平均误码率BER(Bit Error Rate)与迭代次数的关系曲线如图1所示。仿真中各用户信噪比SNR(Signal to Noise Ratio)相同并固定在14 dB，其他参数为：K=10时，SN=10，MCN=100，limit=10，MR=0.4，α=0.5；K=20时，SN=20，MCN=200，limit=20，MR=0.4，α=0.5。

从图1可以看出，由于更强的全局性能和多维邻域搜索策略，EDBABC-MUD的收敛速度最快；PBIL-MUD收敛速度次之，但由于PBIL算法易陷入局部最优，使得PBIL-MUD并未收敛到零；BinABC-MUD具有最慢的收敛速度，如K=10时，EDBABC-MUD迭代12次即可收敛，而BinABC-MUD则需要迭代48次，EDBABC-MUD的速度是BinABC-MUD的4倍。K=20时，BinABC-MUD需要181次才能收敛而EDBABC-MUD只需要21次，EDBABC-MUD的速度是BinABC-MUD的8.6倍。BinABC-MUD要想获得更好的收敛性能，必须增加MCN或者SN。

Figure 1 Curves of convergence performance图1 收敛性能曲线

6.2 误码率性能

设各用户的SNR相同，均从0 dB变化到20 dB，通过统计各用户的平均误码率BER检验各种检测器在不同信噪比下的误码率性能，仿真结果如图2所示。仿真参数为：K=10时，SN=10，MCN=50，limit=10，MR=0.4，α=0.5；K=20时，SN=20，MCN=50，limit=10，MR=0.4，α=0.5。

Figure 2 Curves of BER performance图2 误码率性能曲线

从图2可以看出，Match检测器受多址干扰影响较大，性能最差；PBIL-MUD由于未收敛到零，误码率性能也较差；BinABC-MUD的BER性能改善不明显，在SNR达到一定值后，BER基本趋于平稳，没有明显下降，这主要是由于在较低SN或MCN条件下，BinABC-MUD并未收敛造成的。BinABC-MUD要想获得更好的误码率性能需要增加MCN或者SN。更高的MCN或者SN意味着更高的复杂度；Decorr也具有较好的误码率性能；EDBABC-MUD由于具有较快的收敛速度，随着SNR的增加，BER下降最快，性能最接近OMD。

6.3 抗远近效应性能

将移动台离基地的远近转化为各移动台发送功率的大小[19]。目标用户1的SNR固定在6 dB，干扰用户的SNR从6 dB变化到14 dB以得到不同的远近比，其它仿真参数与图2相同。通过统计目标用户1的BER以检验各种检测器中用户1的抗远近效应的能力，所得结果如图3所示。从图3可以看出，所有检测器中EDBABC-MUD抗远近效应能力最强，最接近OMD，原因是EDBABC-MUD是基于OMD模型的，OMD具有最佳的抗远近效应能力，所以EDBABC-MUD也具有很好的抗远近效应能力。

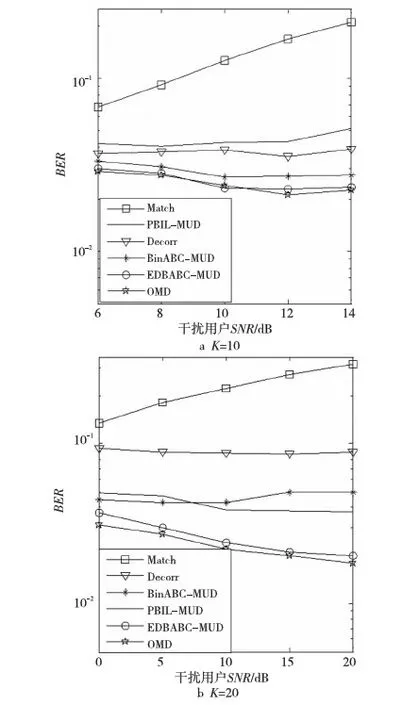
Figure 3 Curves of near-far resistance图3 抗远近效应性能曲线

7 复杂度分析

下面对EDBABC-MUD的计算复杂度进行分析。

算法复杂度主要取决于乘法的次数。EDBABC算法中涉及乘法的有：计算适应度值、计算转移概率和更新概率矢量，其中计算转移概率和更新概率矢量的计算量与适应度值计算相比，可忽略不计。EDBABC-MUD算法共有三次适应度值计算，其计算量约为：

QEDBABC-MUD≈MCN×SN×3Qf×N

(20)

其中，N为每个用户发送的数据量，Qf为利用式(5)计算目标函数值的计算量。

最优多用户检测的计算量约为：

QOMD=2K×Qf×N

(21)

(22)

因此，EDBABC-MUD的计算量直接取决于MCN和SN，由收敛性能的仿真参数可得当SN=K时，MCN≈K，即：

(23)

上式说明，与最优多用户检测相比，EDBABC-MUD算法复杂度降低，例如K=20时，EDBABC-MUD的计算复杂度降低约873倍。

8 结束语

人工蜂群算法利用种群的个体信息实现寻优，具有较好的局部开采能力。本文充分利用分布估计算法可获得全局群体信息与二进制人工蜂群算法可获得局部个体信息的优势，将二者有机结合，提出了一种改进二进制人工蜂群算法。为了加快收敛速度、降低计算复杂度，改进算法采用直接针对离散域的多维邻域搜索策略，避免了连续域到离散域的转换。并将改进算法应用于求解多用户检测问题，提出了一种基于分布估计二进制人工蜂群算法的多用户检测算法，实验结果验证了算法的有效性。

[1] Verdú S.Minimum probability of error for asynchronous Gaussian multiple-access channels[J]. IEEE Transactions on Information Theory, 1986, 32(1):85-96.

[2] Yu Yang,Yin Zhi-feng,Tian Ya-fei.Multiuser detector based on adaptive artificial fish school algorithm[J]. Journal of Electronics and Information Technology, 2007, 29(1):121-124.(in Chinese)

[3] Xu C, Maunder R G, Yang L L, et al. Near-optimum multiuser detectors using soft-output ant-colony-optimization for the DS-CDMA uplink[J]. IEEE Signal Processing Letters, 2009, 16(2):137-140.

[4] Soo K K, Siu Y M, Chan W S, et al. Particle-swarm-optimization-based multiuser detector for CDMA communications[J]. IEEE Transactions on Vehicular Technology, 2007, 56(5):3006-3013.

[5] Liu Hong-wu,Feng Quan-yuan.Particle swarm optimization-based and receive-diversity-aided multiuser detection for STBC MC-CDMA systems[J]. Journal of Electronics and Information Technology, 2009, 31(1):45-48.(in Chinese)

[6] Karaboga D. An idea based on honey bee swarm for numerical optimization[R]. Technical Report-TR06, Kayseri, Turkey:Erciyes University, 2005.

[7] Luo Jun, Wang Qi-ang, Fu Li. Application of modified artificial bee colony algorithm to flatness error evaluation[J]. Optics and Precision Engineering, 2012, 20(2):422-430.(in Chinese)

[8] Karaboga D. A new design method based on artificial bee colony algorithm for digital IIR filters[J]. Journal of the Franklin Institute, 2009, 346(4):328-348.

[9] Hsieh T J, Hsiao H F, Yeh W C. Forecasting stock markets using wavelet transforms and recurrent neural networks:An integrated system based on artificial bee colony algorithm[J]. Applied Soft Computing, 2011, 11(2):2510-2525.

[10] Karaboga D, Ozturk C. A novel clustering approach:Artificial bee colony (abc) algorithm[J]. Applied Soft Computing, 2011, 11(1):652-657.

[11] Marinakis Y,Marinaki M,Matsatsinis N.A hybrid discrete artificial bee colony-GRASP algorithm for clustering[C]∥Proc of International Conference on Computers Industrial Engineering, 2009:548-553.

[12] Liu Ting, Zhang Li-yi, Bao Wei-wei,et al. Multiuser detection technique based on binary artificial bee colony algorithm[C]∥Proc of the 2nd International Conference on Electronics, Communications and Control, 2012:2037-2040.

[13] Chen Tian-shi, Tang Ke, Chen Guo-liang, et al. Analysis of computational time of simple estimation of distribution algorithms[J]. IEEE Transactions on Evolutionary Computation, 2010, 14(1):1-22.

[14] Karaboga D,Akay B.A modified artificial bee colony(ABC) algorithm for constrained optimization problems[J]. Applied Soft Computing, 2011, 11(3):3021-3031.

[15] Kennedy J, Eberhart R C. A discrete binary version of the particle swarm algorithm[C]∥Proc of IEEE International Conference on Systems, Man, and Cybernetics, 1997:4104-4109.

[16] Pampara G, Engelbrecht A P, Franken N. Binary differential evolution[C]∥Proc of IEEE Congress on Evolutionary Computation, 2006:1873-1879.

[17] Wang Ling, Wang Sheng-yao, Fang Chen. A hybrid distribution estimation algorithm for solving multidimensional knapsack problem[J]. Control and Decision, 2011, 26(8):1121-1125.(in Chinese)

[18] Zhou Ya-lan, Wang Jia-hai, Yin Jian. A discrete particle swarm optimization algorithm based on estimation of distribution[J]. Acta Electronica Sinica, 2008, 36(6):1242-1248.(in Chinese)

[19] Ren Cheng, Tang Pu-ying, Fang Jun. Multiuser detector based on particle swarm optimization with stretching technique[J]. Journal of University of Electronic Science and Technology of China, 2007, 36(5):915-917.(in Chinese)

附中文参考文献：

[2] 俞洋，殷志锋，田亚菲．基于自适应人工鱼群算法的多用户检测器[J]．电子与信息学报，2007，29(1)：121-124．

[5] 刘洪武，冯全源．分集接收的STBC-MC-CDMA系统中基于PSO算法的多用户检测[J]．电子与信息学报，2009，31(1)：45-48．

[7] 罗钧，王强，付丽．改进蜂群算法在平面度误差评定中的应用[J]．光学精密工程，2012，20(2)：422-430．

[17] 王凌，王圣尧，方晨．一种求解多维背包问题的混合分布估计算法[J]．控制与决策，2011，26(8)：1121-1125．

[18] 周雅兰，王甲海，印鉴．一种基于分布估计的离散粒子群优化算法[J]．电子学报，2008，36(6)：1242-1248．

[19] 任诚，唐普英，方峻．拉伸技术粒子群优化算法的多用户检测器[J]．电子科技大学学报，2007，36(5)：915-917．