卫星姿态数据的自动处理

李奇，王鹏波，邓国臣

（1.61206部队，北京 100042；2.61540部队，西安 710054；3.61618部队，北京 102102；4.中国测绘科学研究院，北京 100039）

1 引 言

卫星姿态数据存在两种格式：欧拉角和四元数方式。欧拉角方式的姿态数据是通过3个姿态角（滚动角、俯仰角和偏航角）来描述卫星本体坐标系统到卫星轨道坐标系统的转换。四元数方式的姿态数据是通过4个元素构成的单位向量来描述卫星本体坐标系统到地球惯性不变坐标系统的转换。四元数与欧拉角方式的姿态数据存在一一对应的转换关系，其转换涉及到卫星轨道坐标系统到地球惯性不变坐标系统的转换。

本文为了说明问题，以天绘一号卫星（TH－1）的姿态数据为例进行分析，处理过程中用到的姿态数据均以四元数的方式给出。本文通过对姿态数据跟踪发现，星敏数据存在少量的噪声点或零值现象，分析原因是其在接收时，由于受到外界干扰，例如大风或其他原因引起接收器震荡不稳，或受到异常电磁脉冲影响，导致产生随机噪声。由于随机噪声的产生原因复杂，难以归纳噪声点出现的特征规律，而星敏数据的精度要求较高，数据质量的好坏对于影像产品的几何精度影响非常大，所以在这里研究卫星姿态数据的自动处理技术，提高卫星姿态数据的质量，具有重要的实用价值。

2 TH－1卫星姿态数据分析

为简化问题模型，本文以某次拍摄任务的一个星敏数据为例，对姿态数据的自动处理进行研究。

2.1 姿态数据的整体情况分析

绘出原始星敏数据的散点图，其整体情况如图1所示。

通过这些图得知，四元组的整体情况为趋于平滑的曲线。但存在部分噪声点或异常点。这样的q值，在计算过程中，会导致图像生产的过程中严重出错或出现图像内部畸变，因此在解析后需要将这些点滤掉。

2.2 姿态数据的局部情况分析

通过分析姿态数据的局部情况可知，其q值与时间的变化如图2所示。

在局部分析中发现星敏的阶跃是一种普遍现象，每4个点附近都要发生一次。根据数据格式规范，下行数据的每个点值都重复4次记录，对于这种情况，合理的处理方式是必须去掉重复和错误的点值，并且利用曲线拟合的方法获取给定时间的四元数。

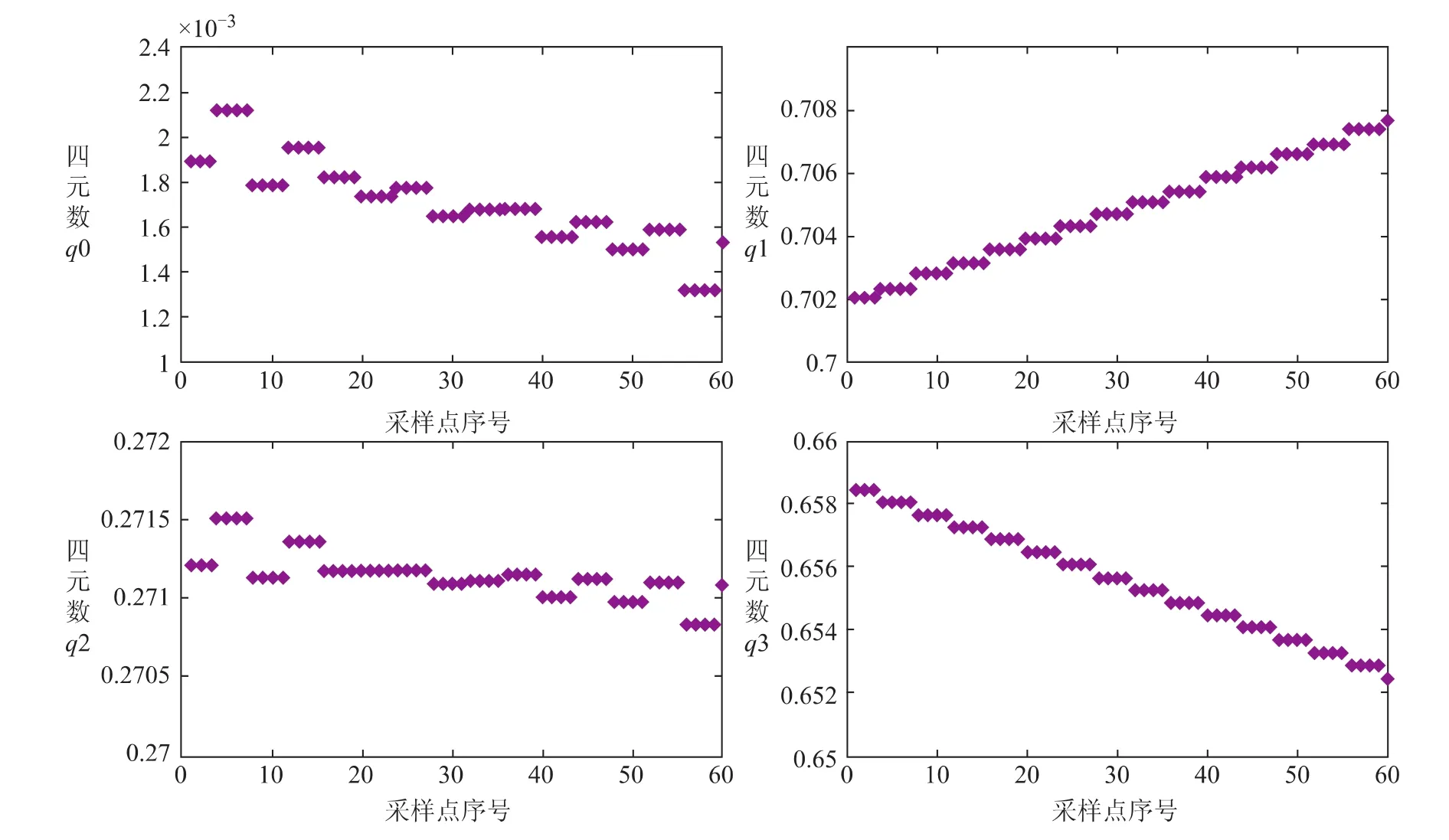
图2 星敏四元数的局部效果图

2.3 姿态数据的规律特性分析

通过对姿态数据的深入分析，可以总结出数据具备以下特点：

（1）噪声数据的跳变特性

通过图1可以看出，发生跳变的噪声点值与实际值偏差较大，这种粗差应通过滤波的方式将其删除，以免对其他观测值造成影响。

（2）采样点重复记录

通过图1可以看出，对于同一个时刻的星敏数据，重复采样了4次，因此需要在处理前去掉重复点。

（3）观测数据的时间等距特性

根据数据格式规范和星敏试验数据的实际内容可以看出，除了漏接或重复记录的时间段外，观测数据的采样时间间隔是固定的（0.5s）。

（4）数据的连续特性

根据图1、图3可以看出，观测数据在整体上是一条趋于平滑的曲线，根据天体运动相关原理，星敏四元数的实际数值（即真值）应平滑变化，不应发生跳变，因此可以通过拟合的方式，对原始星敏数据的质量进行优化。

图3 初始化后的队列行时标

3 技术与方法

根据前面分析的观测数据的特征规律，制定了相应的解决方案，具体步骤如下。

①载入姿态数据；

②去重和补空。采用投票方式，将重复的、不可信的数据剔除。检测时标数据的连续性，将漏接时间的对应数据标记为“null”（空）；

③去噪。目的是将原始星敏数据中的噪声剔除，并将其数值标记为“null”，使其不能参与拟合过程，以免影响多项式拟合的精度；

④拟合。分别对星敏的各个分量采用整轨二次多项式曲线拟合的方法，以获取更加平滑的姿态数值，消除数据抖动对图像产品带来的弯曲和内部畸变现象；

⑤结果输出。

3.1 姿态数据的去重和补空

由于姿态数据存在重复和漏接问题，因此在数据去噪和拟合之前，应先解决这方面的问题，本文设计了对应方案，具体步骤如下。

①载入姿态数据；

②初始化队列数据。队列数据是由一系列数据包组成的序列，每个数据包中包含行时标信息和这个行时标所对应的各个星敏的四元数信息。这个步骤的主要工作是依据原始星敏数据中的起止行时标信息，确定队列数据的队列长度，给行时标数据赋值（步长为0.5s递增），然后将每个行时标对应的各个星敏的四元数信息都标记为“null”；

③姿态数据的去重。在本文中，去重工作主要是依据投票原理进行。同一时标被重复记录4次，将4次的星敏四元数大小进行比较，相等次数最多的那个数值被解释为可信度最高，将其赋值给队列中相同行时标对应的星敏四元数，如果没有找到，则跳过，进行下一步星敏数据的去重，直到结束。

3.2 姿态数据的去噪

姿态数据去噪的目的是将发生跳变的异常数据剔除，只留下有效的星敏数据，以免影响拟合多项式的精度。

综合考虑姿态数据变化速度缓慢的规律特征，本文采用递推差值的方法去除噪声。根据实际数据统计发现，相邻两组星敏数据差值的绝对值大小都在某一狭窄区间内。将队列内的星敏数据依次做减法运算，并根据不同差值做相应处理，很好的完成了姿态数据噪声的去除，具体流程如图4所示。其中，Qj为待处理的星敏数据序列，Δ表示两次星敏采样数据的差值，Ω为相邻两次星敏采样数据的差值空间。

需要注意的是，当流程图中j－i＞0时，表示数据中连续出现空值点的个数大于1，因此Δ允许的数值范围也需扩大相应倍数，在流程图中以“Ω×（j－i＋1）”形式表示。

3.3 姿态数据的自动修复

经过前面的去重、补空和去噪处理，当前队列中除了空值外，其余数据都为有效数据。根据星敏数据的散点图可以看出，当拟合多项式的次数为2时，拟合函数就可以很好的描述星敏数据的轨迹曲线。

本文的解决思路是采用最小二乘法对有效的星敏数据进行二次多项式拟合，求出拟合多项式，最后将所有行时标重新代入拟合多项式，求出对应时刻的星敏数据，即完成了姿态数据的自动处理。

图4 姿态数据的自动去噪

假定行时标用xi（i＝0，1，…n）表示，对应时刻的星敏四元数用yi（i＝0，1，…，n）表示，需要拟合的有效数据个数为n，构造函数f（x）＝a0＋a1x＋a2x2，式中，a0、a1、a2为多项式系数，满足

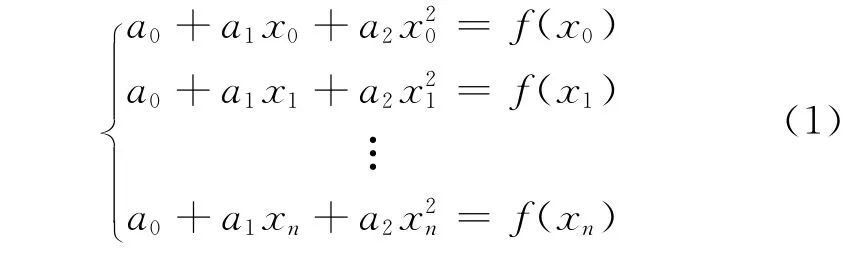
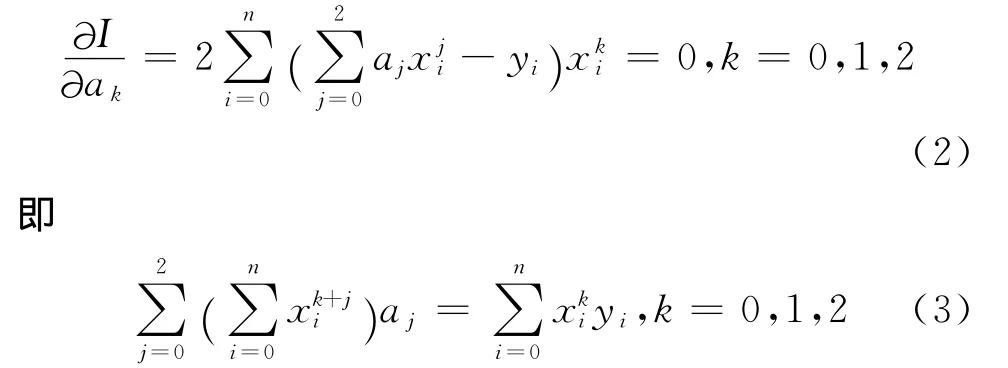
式（3）是关于a0、a1、a2的线性方程组，用矩阵表示为

解方程组即可得出多项式系数a0、a1、a2的值。

4 实验验证

为明确测量值与拟合值的偏离程度，本文随机对采样数据中连续10个采样点做了记录，具体结果如表1所示。

下图是对星敏数据进行自动处理后的效果展示。

从处理后的星敏数据散点图可以看出，与处理前相比：

①处理后数据消除了重复数据和噪声数据，提高了数据整体的可信度；

②处理后数据在整体分布上更均匀，过渡更加平滑；

表1 星敏数据自动处理效果实验对比

图5 星敏四元数的处理后整体效果图（与图1对应）

图6 星敏四元数处理前后局部对比图（采样点序号0∶60）

③该方法对于局部有抖动现象的数据（如四元数q0、q2）质量明显改善。

5 结束语

本文针对TH－1卫星下传的姿态数据进行了深入分析，通过设计合理方案，实现了对原始星敏数据的自动去重、补空、去噪和拟合。通过实验验证，姿态数据经过处理后，不仅能够完全去除噪声点和重复记录的数据，而且还可以通过拟合的方式将短时间漏接的数据还原，数据质量有明显改善。通过该方法生产处理的姿态数据可直接用作卫星数据的定姿计算。

下一步的研究方向：

（1）采用高次（3～8次）多项式拟合的方法对姿态数据进行拟合，研究拟合函数的次数对于拟合结果的影响情况，深入分析不同情况下的精度偏差情况，选取更合理的拟合方法；

（2）本文只是针对1次拍摄任务的姿态数据进行研究和处理，下一步要增加试验数据的采样范围，将时间跨度增加到2个月甚至更长，进一步研究姿态数据变化的周期性规律；

（3）如果姿态数据中漏接的时间段较长，肯定会影响拟合精度，不同时间长短的影响程度是多少，如何建立一套科学合理的精度评估系统，也是下一步研究的重点。

［1]刘念.最小二乘插值与拟合推估［J］.测绘科学，2002，27（3）：19－21，51.

［2]齐林，周丽晓.变换域自适应滤波算法的研究［J］.郑州大学学报（理学版），2007：39（1）：61－66.

［3]黄贤源，隋立芬，范澎湃.几种最优滤波方法的分析和比较［J］.测绘工程，2007，16（3）：35－39.

［4]王晶昕.样条插值适定性与插值逼近问题研究［D］.大连：大连理工大学，2004.

［5]何洪英，姚建刚，罗滇生.红外图像的自适应混合消噪方法［J］.计算机工程与应用，2006（6）：7－9.