低碳经济背景下的国际博弈及对中国的启示

樊 元，周 巍

（西北师范大学 经济学院，兰州 730070）

低碳经济背景下的国际博弈及对中国的启示

樊 元，周 巍

（西北师范大学 经济学院，兰州 730070）

“低碳经济”作为 21世纪出现的新名词，涉及到了经济、政治、科技、环保等诸多领域。各国围绕低碳经济在相关领域的博弈错综复杂，利益集团的形成在所难免。然而，利益诉求的重叠也使得合作的必要性同时存在，如何建立相互信任的合作框架实现双赢关系到我们的生存环境以及实现可持续发展，谋求公平的国际话语权等一系列问题，值得分析和探讨。围绕“低碳经济”所牵涉到的各种因素，将其中一些关键影响因素抽取出来，建立静态博弈模型和演化博弈模型，分析发达国家群体和发展中国家群体在发展低碳经济中的利益趋同与分歧，可找到博弈收敛的稳定均衡点，得出发达国家群体和发展中国家群体只有相互合作才能实现最优的博弈结果这一结论。同时，博弈结果表明，切实有效的法律框架以避免“免费乘车者”是促成合作有效的基础，这些将对中国发展低碳经济给予有益的启示。

低碳经济；发达国家；发展中国家；纳什均衡；演化博弈

一、引言与文献综述

人类近一个多世纪以来的活动已引起全球温室气体浓度不断增加，由此所带来的“温室效应”使全球气温不断上升并可能对地球气候造成一系列的不利影响。2003年英国政府在其能源白皮书《我们能源之未来：创建低碳经济》中首次提出“低碳经济”的概念，指通过提高资源的生产率，以更少的自然资源消耗和环境污染获得更多的产出，从而创造高水平、高质量的生活。

如今“温室效应”问题已经成为全球关注的焦点，各个国家在国际气候大会上唇枪舌剑，针对发展低碳经济进行了一轮又一轮的博弈但却进展缓慢。各国在谈判中谋求各自的政治、经济利益，同时，又由于各个国家的发展差异，利益诉求的不同，形成了不同的利益集团。其中，以发达国家和发展中国家的博弈最为突出和重要。

发达国家大都完整经历了历次工业革命，完成了城镇化，在发展低碳经济上担任着推动者和领导者的角色，而发展中国家大都处于工业化、城镇化发展中期，对能源的需求更大，并且低碳技术积累薄弱，处于高碳排放的发展模式。一方面，发达国家企图推卸、淡化因历次工业革命而产生的大量温室气体排放的历史责任，通过征收碳关税，以及开展国际低碳产品认证等变相的贸易保护主义手段向发展中国家施压，希望发展中国家跟发达国家一样接受强制减排规定[1]；另 一 方 面，发 展 中 国 家 为 了 自 己 的生存发展，坚持《联合国气候变化框架公约》中所提出的“共同但有区别的原则”，不接受量化的强制减排，并希望发达国家在转移低碳技术以及出资支持发展中国家应对低碳减排问题上拿出更多诚意，同时也要采取措施应对发达国家的“低碳陷阱”[2]。

无论是《京都议定书》签订后美国的退出，还是哥本哈根会议、坎昆会议、德班会议、多哈会议乃至华沙气候大会，发达国家与发展中国家的博弈始终在继续，关于低碳减排的进程步履维艰。

纪明（2011）对国际碳博弈中形成的利益集团进行了分析和探讨，阐明了利益集团之间的分歧和交集[3]；石红莲（2013）采用完全信息条件下的静态博弈和动态博弈模型，分析了中美之间存在的低碳博弈问题[4]；王 京 安 （2012）采 用 演 化 博 弈 模 型，分析了国内 政 府 和 企 业 之 间 的 低 碳 博 弈[5]。目 前 关于低碳经济方面的博弈模型文献大多采用的是基于完全理性的静态或者动态模型，这不太符合现实中的大多数情况，因为低碳博弈涉及到经济、政治等诸多因素，是一个复杂的过程，通过一次静态博弈得出的结果显然说服力不够。

Hirshleifer（1982）提 出 了 演 化 均 衡 的 概 念。 他认为若从动态系统的某平衡点的任意小邻域内出发的轨线最终都演化趋向于该平衡点，则称该平衡点是局部渐近稳定的，这样的动态稳定平衡点就是演化均衡[6]。王文宾 （2009）提 出演化稳定 策 略 是 纳什均衡的精炼这样一个概念[7]。

Friedman（1998）指出：纳 什均衡是动 态 系 统 的平衡点；演化均衡一定是纳什均衡；演化稳定策略不一定是演化均衡。复制者动态方程可以保证演化稳定策略为演化均衡，但对一般的动态方程来说演化稳定策略不 是 演 化 均 衡 的条件[8]。黄 凯 南 （2009）讨论了演化博弈和演化经济学的区别和联系[9]。

目前，采用演化博弈模型分析发展中国家和发达国家群体在低碳减排方面的博弈文献还较少，因此本文试图运用演化博弈模型，进行深入分析讨论，以期得到两群体博弈的演化稳定策略。

二、基于静态博弈的混合策略纳什均衡

（一）假设

1992年《联合国气候变化框架公约》的签署确立了“公平性原则”和发达国家与发展中国家在应对气候变化中“共同但有区别的责任原则”。而且根据《联合国气候变化框架公约》，各国经过十多年的努力，签订了第一个控制温室气体排放的、具有约束力的国际协议《京都议定书》。但是，在数十年的关于发展低碳经济，进行低碳减排的历次气候环境谈判中，以欧美为代表的发达国家一直操控着领导权和话语权，一方面没有积极执行公约中的减排义务，另一方面向中国为代表的发展中国家施加压力，要求发展中国家承担更多的减排责任。因此，发展中国家也要积极团结起来，坚持联合国公约中“共同但有区别的责任”原则，维护自身的利益，积极地与发达国家进行碳博弈。

尽管各国对气候变化带来的影响和应对手段尚有不同看法，但通过合作和对话、共同应对气候变化带来的挑战是大家的基本共识。此外，发展中国家需要在国际碳博弈中获得更多的资金、技术援助，同时拥有更多的话语权和定价权。因此，应对全球气候变暖的决策与行动不能仅仅依靠于发达国家主观臆断，而应该是国际间碳博弈的结果[3]。

我们假设：

1．博弈方为发达国家和发展中国家。两博弈方群体并不会一开始就找到最优策略或者说至少有部分博弈方不会采用完全理性的博弈均衡策略，这是双方相互学习和模仿，均衡不断调整和改进而不是一次选择的结果[11]。

2．发达国家策略为：发达国家积极发展低碳经济并积极向发展中国家输出低碳技术和资金同时加大对发展中国家不作为的监督处罚力度，记为策略1；反之，发达国家安于现状，不积极同发展中国家开展低碳经济合作，记为策略 2[3]。

3．发展中国家策略为：发展中国家积极同发达国家合作，积极开展碳交易，记为策略 3；发展中国家安于现状，追求短期经济利益，对于发展低碳经济，同发达国家进行低碳合作的积极性不高，记为策略 4[3]。

4．设发达国家和发展中国家发展经济每单位利润分别为 UA和 UC，我们可以认为这里的每单位是同质的产品或服务。

5．发展中国家积极发展低碳经济，发达国家会给予发展中国家每单位 s的补贴，这里的补贴代表低碳资金以及技术支持；发展中国家不发展低碳经济，发达国家会对发展中国家每单位征收 t大小的碳关税作为惩罚[4]。

6．若发达国家不发展低碳减排，不积极输出低碳技术和资金，则会受到国际舆论谴责，因此会损失一定的国际声誉，每单位损失记为 f。

7．若双方都发展低碳经济，则各自的单位利润将会增加 a倍。显然 a＞1，即我们认为发展低碳经济是能够促进经济发展的，因为低碳经济是以低能耗、低排放、低污染为基础，以提高能源利用效率和创建清洁能源为目的的，因此它实现了可持续发展，能在未来获得丰厚的利润回报。

8．博弈双方中有一方发展低碳经济，另一方不发展低碳经济，则发展低碳经济国家每单位利润会增加 b倍，不发展低碳经济国家每单位利润会减少为原来的b倍。同时发展中国家和发达国家若发展低碳经济，则每单位低碳投入成本分别记为 CC和CA。显然 b＞1，道理同假设 7中所述，但 a＞b因为此时博弈双发并未展开合作因此需付出更多成本。同时有 c＜1因为不发展低碳经济是不可持续的发展模式，长期下去不发展低碳经济国家产品受到发展低碳国家产品竞争挤压，利润会逐渐受到压缩。故有 a＞b＞1＞c。

9．本模型着重阐述发达国家和发展中国家发展低碳经济的策略互动，故不考虑双方合作时自身也积极发展低碳经济上的投入成本。

假设发达国家采用策略 1概率为 x，策略 2概率为 1－x，发展中国家采用策略 3概率为 y，策略 4概率为 1－y，构造博弈矩阵如表1。

表1 静态博弈的收益矩阵

（二）混合策略纳什均衡

我们接下来进行均衡的计算。

给定 y，发达国家选择策略 1（发展低碳经济）和策略 2（不发展低碳经济）的期望收益分别为：

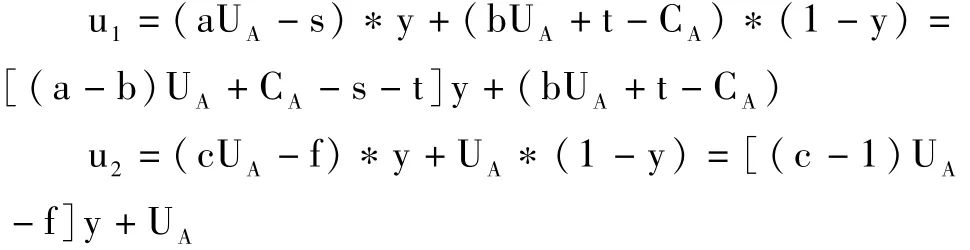
令 u1＝u2，解得：

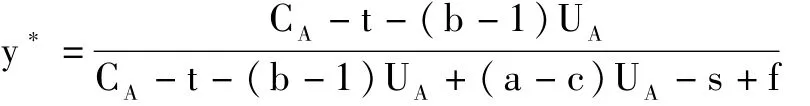
因此，当 y＞y*时，发达国家将积极发展低碳经济，对发展中国家转移低碳技术和资金支持；当 y＝y*时，发达国家将相机选择；当 y＜y*时，发达国家将不参与发展低碳经济，也不积极对发展中国家转移低碳技术和资金支持。

给定 x，发展中国家选择策略 3（发展低碳经济）和策略 4（不发展低碳经济）的期望收益分别为：

令 u3＝u4，解得：

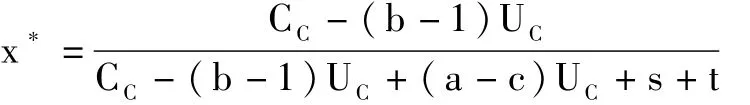
因此，当 x＞x*时，发展中国家将积极发展低碳经济，同时积极接受发达国家的低碳技术和资金支持；当 x＝x*时，发展中国家将相机选择；当 x＜x*时，发展中国家将不参与发展低碳经济，也不积极接受发达国家援助。

综合上述结果，可得纳什均衡解为

只有当 x*，y*均处于[0，1]区间时，混合策略的纳什均衡解才存在。下面重点讨论 x*，y*均处于[0，1]区间时的情况。

即当 1＞x＞x*＞0并且 1＞y＞y*＞0时，发达国家和发展中国家都将积极发展低碳经济，展开广泛的低碳技术和市场上的合作而实现共赢，全球气候合作将朝着有利的方向发展。我们已知 x，y分别表示发达国家和发展中国家选择某种策略的概率，因此它们均处于[0，1]区间，要使 x落在[x*，1]以及 y落在[y*，1]的概率越大，我们就要使 x*，y*的值越小，它们越趋近于 0，x落在[x*，1]以及 y落在[y*，1]的概率就越大，发达国家和发展中国家都将积极发展低碳经济，开展合作的可能性就越高。

三、非完全理性的动态演化博弈

（一）假设

静态博弈仅仅是一次博弈的结果，双方同时参与博弈没有先后之分，并且假设参与方均完全理性，这点在现实中并不符合大多数情况。发达国家和发展中国家是在不断策略互动的，发达国家希望通过碳交易来降低国内的减排成本，而发展中国家则希望获得发达国家更多的低碳技术与资金支持，这种策略互动是一个不断演化的进程，这需要发达国家和发展中国家共同的努力和理性的参与。发达国家进行低碳技术转移与资金支持的诚意不够或者发展中国家追求经济发展短期利益而进行低碳发展的积极性不高都有可能使低碳经济合作陷入困境。发达国家和发展中国家彼此之间的选择是与对方的策略函数密不可分的，因此我们继续采用演化博弈模型进行分析。

演化博弈模型的假设：此时的博弈双方是发展中国家和发达国家两个群体，并且两博弈方群体并不会一开始就找到最优策略或者说至少有部分博弈方不会采用完全理性的博弈均衡策略，这时双方相互学习和模仿，均衡不断调整和改进而不是一次选择的结果[10]。其他假设同二、（一）假设中的 2－9。

假设发达国家群体采用策略 1的比例为 x，策略 2的比例为 1－x，发展中国家采用策略 3的比例为 y，策略 4的比例为 1－y，构造博弈矩阵如表2。

（二）局部均衡点

模仿生物进化博弈的“进化稳定策略”（Evolution-ary Stable Strategy，ESS），我们试图得到博弈双方的复制动态方程，即表示博弈方模仿学习的速度方程。

表2 非完全理性博弈的收益矩阵

发展中国家采用策略3的复制动态方程为：

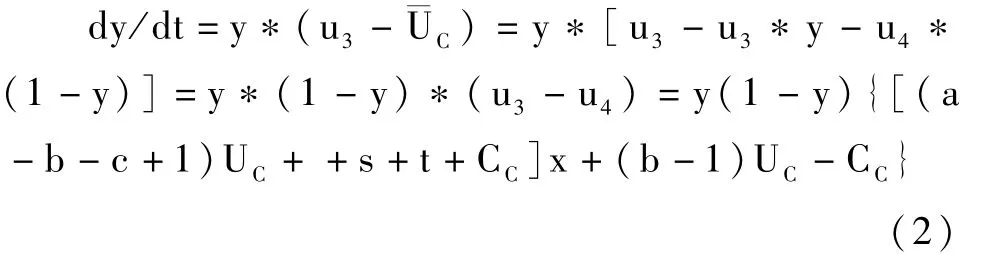
微分方程（1），（2）所构成的方程组描述了发达国家和发展中国家演化博弈的动态过程，我们可以对其联立求解，得到五个局部均衡点，分别为 E1（0， 0），E2（0，1），E3（1，0），E4（1，1），E5

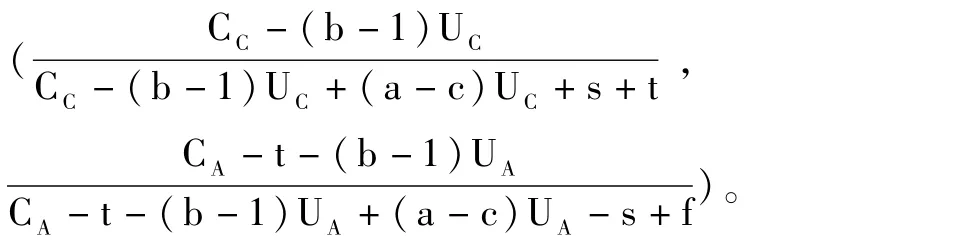
对于微分方程组（1），（2）所描述的群体动态演化过程，我们可以采用 Friedman提出的方法对均衡点的稳定性进行分析。即通过考察动态系统方程组的雅 各 比 （Jacobian）矩 阵 确 定 演 化 稳 定 性 策 略（ESS）。如果矩阵行列式的符号为正，而且矩阵迹的符号为负，则表明相应的均衡点具有渐进稳定的性质；如果矩阵行列式的符号为正，且矩阵的符号为正，则表明相应的均衡点不具有稳定性；如果矩阵行列式的符号为负，则表明相应的均衡点是鞍点[11]。

由此，我们可以得到上述动态微分方程组（1），（2）的雅各比（Jacobian）矩阵为

把上述五个均衡点的结果代入该雅各比矩阵，结果如表3，

表3 演化博弈的局部均衡稳定性分析判断方法

（三）稳定的局部均衡点

按照前面 Friedman提 出 的 判 断 均 衡 点 的 稳 定性的方法进行分析，我们分不同情况分别计算相应条件下的雅各比 （Jacobian）矩 阵，由 此 试 图 找 出 稳定的均衡点，经计算，我们发现：

1．aUA－s＞cUA－f，bUA＋t－CA＜UA且 bUC－CC＜UC时，渐进稳定的均衡点 ESS为（0，0）和（1，1），即博弈双方策略组合为（不发展低碳经济，不发展低碳经济）和（发展低碳经济，发展低碳经济）。

2．aUA－s＞cUA－f，bUA＋t－CA＜UA且 bUC－CC＜UC时，渐进稳定的均衡点 ESS为（1，1），即博弈双方策略组合为（发展低碳经济，发展低碳经济）。

3．aUA－s＞cUA－f，bUA＋t－CA＞UA且 bUC－CC＜UC时，渐进稳定的均衡点 ESS为（1，1），即博弈双方策略组合为 （发展低碳经济，发展低碳经济）。

4．aUA－s＜cUA－f，bUA＋t－CA＜UA且 bUC－CC＜UC时，渐进稳定的均衡点 ESS为（0，0），即博弈双方策略组合为（不发展低碳经济，不发展低碳经济）。

5．aUA－s＜cUA－f，bUA＋t－CA＞UA且 bUC－CC＜UC时，不存在稳定均衡点。

6．aUA－s＜cUA－f，bUA＋t－CA＞UA且 bUC－CC＞UC时，渐进稳定的均衡点 ESS为（0，1），即博弈双方策略组合为（不发展低碳经济，发展低碳经济）。

我们若同时采用二、（二）中静态分析的方法对博弈模型进行分析，对应各种情况下的纳什均衡，发现结果和演化稳定策略组合及渐进稳定状态相一致，这也 一 定 程 度 上 印 证 了 Friedman（2008）[8]，王文宾（2009）[7]等人理论的正确性。

对上述 6种情况进行总结，1、2、3情况下，有aUA－s＞cUA－f，即发达国家发展低碳经济的收益大于不发展低碳经济的收益，这时一定存在（发展低碳经济，发展低碳经济）的策略组合。在这时，发达国家无论发展中国家策略如何，发达国家都乐于开展低碳经济合作，而且也能实现与发展中国家的合作。发达国家考虑到了发展低碳经济在未来所带来的巨大的经济利润回报以及能源利用效率的提高和生态环境的极大改善，以及不发展低碳经济在国际政治中所受到的国际舆论的巨大谴责压力，终于拿出了与发展中国家合作发展低碳经济的诚意。

在 4情况下，发达国家和发展中国家都不愿进行低碳经济方面的发展和合作。这时，发达国家和发展中国家考虑到发展低碳经济的巨大投入成本以及可能的市场风险，都采取了保守的策略，维持现有的经济发展模式，博弈陷入“囚徒困境”，地球大气环境更加恶化，人类生存面临更大挑战。

在 5情况下，发展中国家在国际上对发达国家的话语权影响力很小，或者发展低碳经济的经济效益短期内还不够明显，使发展中国家缺乏同发达国家合作的意愿，同时发展中国家自身考虑短期经济利益以及发展低碳经济的机会成本，不发展低碳经济。发达国家只好独立发展低碳经济，发展中国家则充当“搭便车”的角色，国际上缺乏一个强有效的机制对所有国家进行监督，处于无序状态。

在 6情况下，发达国家不发展低碳经济，而发展中国家积极发展低碳经济。造成这种情况的原因可能是低碳经济短期内并未带来大的经济效益或者说发展中国家内部不够团结，在国际上对发达国家的话语权影响力微乎其微，处于弱势地位。发达国家通过向发展中国家转移低碳技术和资金支持，同时采取碳关税等强制性措施促使发展中国家发展低碳经济，节能减排。

（四）演化路径分析

我们发现，在第 1种情况下，博弈存在两个渐进稳定状态即（不发展低碳经济，不发展低碳经济）和（发展低碳经济，发展低碳经济），此时的条件也更加符合现实的经济情况。发展低碳经济的确能够带来巨大的经济回报和环境气候的极大改善，但同时作为资本与技术密集型产业，有着较大的市场风险，需要很大的初期投入以及转型的经济损失，同时由于“搭便车”的存在，因此发展低碳经济是一把“双刃剑”，如何使博弈收敛于最优的稳定均衡点是两个博弈群体不断策略互动的结果。

我们计算判断这种情况下的局部均衡点的稳定性结果如表4。

即系统仅有两个渐进稳定点 E1（0，0），E4（1，1），即发达国家和发展中国家仅有两个稳定的策略均衡（发展低碳减排，发展低碳减排）和（不发展低碳减排，不发展低碳减排）。E2（0，1）、E3（1，0）为不稳定的均衡点，而 E5（x*，y*）为鞍点。

接下来我们用系统动态演化趋势图来描述发达国家和发展中国家两群体的复制动态和稳定性。

表4 1条件下局部均衡点的稳定性

图1 发达国家和发展中国家群体复制动态和稳定性

图1描述了在 aUA－s＞cUA－f，bUA＋t－CA＜UA且 bUC－CC＜UC的条件下演化博弈模型的演化路径。在发展低碳经济这个问题上，发达国家和发展中国家通过演化博弈最终收敛于两种状态，即两群体均不发展低碳经济的 E1（0，0）位置和两群体合作发展低碳经济的 E4（1，1）位置。鞍点 E5（x*，y*）将图中博弈演化区域分成了四个部分，两群体的博弈演化最终收敛的状态取决于博弈开始时初始状态所处的位置。

我们不难发现，当博弈开始时的位置位于 B区域时，x＞x*，y＞y*，博弈最终收敛于 E1（0，0），即发达国家和发展中国家均愿意发展低碳经济，展开合作。当博弈开始时的位置位于 C区域时，x＜x*，y＜y*，博弈最终收敛于 E4（1，1），即发达国家和发展中国家均不愿意发展低碳经济。当博弈开始的位置位于 A区域或 D区域时，即 x＜x*，y＞y*或者 x＞x*，y＜y*，时，此时博弈最终有可能收敛于 E1（0，0），也有可能收敛于 E4（1，1），概率大小取决于鞍点 E5（x*，y*）的位置。

由此我们知道要想博弈尽可能的收敛于最优的E4（1，1）点，我们就要让 B区域的面积尽可能的大，这样博弈开始时落在 B区域的概率就更大，这就和鞍点的位置有关，我们应尽量让 E5（x*，y*）点向左下方移动，尽可能的靠近原点，即我们应让 x*，y*的值尽可能的小，这就涉及到对参数的讨论。

（五）参数讨论

在 aUA－s＞cUA－f，bUA＋t－CA＜UA且 bUC－ CC＜UC的条件下，要让 x*，y*的值尽可能的小，我们已知

经过简单的数学计算推导，我们不难发现：

1．a，b越大，c越小时，x*，y*的值就越小。即发展低碳经济获得的单位利润增长越多，发达国家和发展中国家发展低碳经济展开合作的可能性就越高。

2．CA，CC越小，x*，y*的值就越小。即当单独发展低碳经济的投入成本越小时，任一国家发展低碳经济的可能性就越高，这也是显而易见的。

3．f越大，y*的值就越小。即当发展中国家对发达国家发展低碳经济的不作为的舆论谴责压力越大时，发达国家迫于国际地位形象的损失的机会成本越大，发展低碳经济的可能性就越高。

4．s，t越大，x*就越小。即当发达国家对发展中国家发展低碳经济的扶助力度越大，同时对发展中国家的不作为的监督惩罚力度越大，发展中国家发展低碳经济的可能性就越高。

四、数据分析

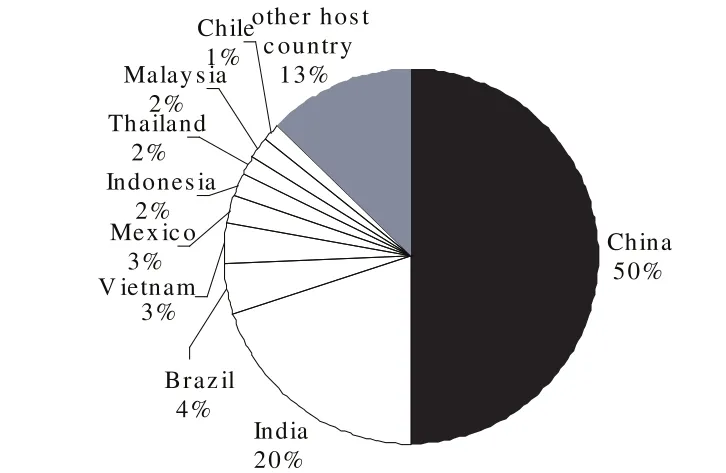
图2 发展中国家 CDM项目累计注册数量比例

由图2可以看出中国 CDM项目累计注册数量比例已居首位，高于第二位的印度近三十个百分点，占据发展中国家市场近一半份额。

由表 5数据不难发现，中国 CDM项目签发获得的 CERs数量占发展中国家总量的百分比自 2006年开始一直保持较快上升势头，通过计算可以得出，目前中国获得签发 CERs总量累 计 为 880530510吨，发展中国家获得签发 CERs总量为 1458416551吨，中国累计所占比例为 60．38%，已经达到了一个很高比例。

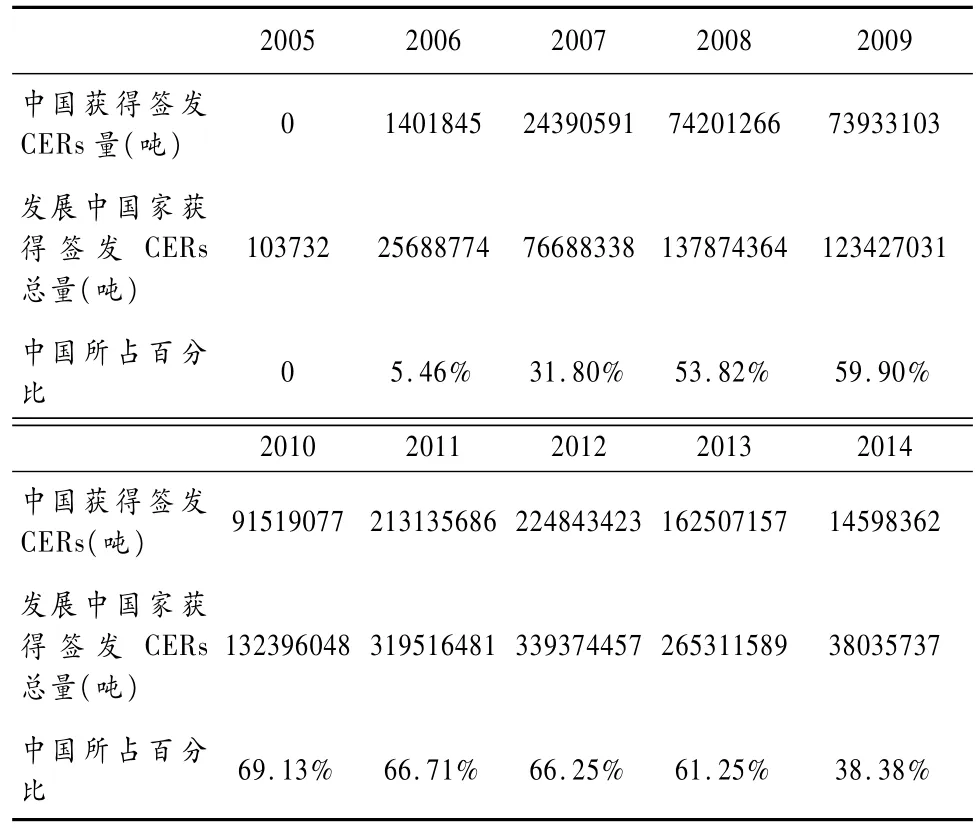
表 5 中国 CDM项目签发获得 CERs数量百分比

由图2和表5可见我国在积极开展低碳技术国际合作上的努力，并且已经取得了不错的成绩。

图3 发展中国家 CDM项目签发获得 CERs比例（百分比）

由图3可以发现，从 2006年开始，中国不论在CDM签发增速还是规模上，都遥遥领先于其他发展中国家，到 2012年达到一个峰值，随后在 2013年有一个较大下滑，到 2014年下滑幅度更大，其他发展中国家情况也是如此，在 2013年、2014年 CDM项目签发均呈下降情况，这反映了国际低碳市场的不稳定性，国际低碳经济合作需要更稳定而有效的合作框架机制。

以上是中国积极参与国际合作的 CDM项目数据信息，国内方面中国也在积极发展低碳经济，建立自己的碳交易市场。国家发展改革委批准的国内CDM项目累计已达 5058个，截至今年 5月 23日，我国碳交易累计成交 385万吨，交易金额为 12501万元，成为继欧盟之后的全球第二大碳交易市场（数 据 来 源 为 中 国 清 洁 发 展 机 制 网 http：／／cdm．ccchina．gov．cn／），可见我国构建自己的碳交易市场成果也很显著。

五、结论及对中国发展低碳经济的启示

发达国家作为低碳发起人，在节能减排方面已走在世界前列，因此发展低碳经济继续提升能源利用效率等所需成本较大，发展中国家考虑到低碳经济转型的投入对经济发展增速以及由此带来的失业率上升等因素的影响，单独发展低碳经济所需承担风险也较大。所以发达国家和发展中国家应通过合作来降低成本，CDM机制便是一个好的范例。一方面发达国家以较低成本购买碳排放权完成了减排任务，另一方面发展中国家获得了低碳技术和资金，实现对产业结构的升级与传统产业的改造，提高了效率。

发达国家要切实拿出诚意对发展中国家提供低碳经济合作方面的资金支持和技术援助。发展中国家内部应维护“共同但有区别责任”这一关系发展中国家共同利益的原则，尽可能地团结起来，这样才能在国际碳博弈中获得更多的话语权，形成对发达国家不作为的强大政治舆论压力，才能使博弈朝着合作双赢的方向发展，实现“1＋1＞2”。

到目前为止达成的气候会议协定都不具备法律效力，这给不发展低碳经济的国家提供了“免费乘车”的机会，发达国家和发展中国家应积极努力合作，达成具有法律效力的文件协定，加大监督处罚力度，避免“免费乘车者”。

我国由于自身能源消费结构和产业结构还不够合理，且处在城镇化大发展的关键时期，碳排放的增长已不可避免，因此经济发展还处于“高碳”时期，但我国市场潜力巨大，因此可以给低碳新技术的推广提供很好的试验场地。而发达国家则在人力资本、基础科学研究、把研究中取得的成果商业化应用的能力方面占有相对优势。同时我国也在进行经济社会转型的改革，因此我国应积极与发达国家展开低碳技术方面的合作，积极申请 CDM项目，降低低碳技术研发成本。我国与发达国家一旦合作成功，可以促使低碳新技术的快速推广和应用，形成规模以后就可以大大降低投入成本。

我国也应积极建立自己的碳交易市场，与国际接轨，这样，我国就能为国内企业提供经国际认证的碳指标，使其在国际贸易中避免因碳排放过量问题受到发达国家处罚。同时，我国还应积极联合其他发展中国家，争取在国际碳博弈中拥有更多的话语权。

[1]纪玉山，赵洪亮．维护发展中国家利益，积极与发达国家进行碳博弈[C]／／社会主义经济理论研究集萃：从经济大国走向经济强国的战略思维．北京：经济科学出版社，2011．

[2]王倩，黄蕊，双星．“碳陷阱”：理论辨析与政策导向[J]．经济学家，2011（10）：5．

[3]纪明．低碳经济背景下的碳博弈问题研究[D]．长春：吉林大学，2011．

[4]石红莲，谷溪．基于完全信息假设下的中美碳排放博弈分析[J]．亚太经济，2013（3）：20．

[5]王京安，韩立，高翀，徐昕．低碳经济发展中政府与企业之间的博弈分析[J]．科技管理研究，2012（22）．

[6]Hirshleifer J．Evolutionary Models in Economics and Law：Cooperative Versus Conflict Strategies[J]．Research in Law and Economics，1982（4）．

[7]王文宾．演化博弈论研究的现状与展望[J]．统计与决策，2009（2）：10．

[8]Friedman D．On Economic Applications of Evolutionary Game Theory[J]．Journal of Evolutionary Economics，1998（8）：15-43．

[9]黄凯南．演化博弈与演化经济学[J]．经济研究，2009（2）：20．

[10]谢识予．经济博弈论[M]．上海：复旦 大学出 版社，2009：222-246．

[11]Friedman D．Evolutionary Games in Economics[J]．Econometrica，1991（59）：637-666．

责任编辑：刘洁岷

（E-mail：jiemin2005＠126．com）

The International Gam e under the Background of Developing Low-Carbon Econom y and Revelations to China

FAN Yuan，ZHOU W ei
（School of Econom ics，Northwest Normal University，Lanzhou 730070，China）

“Low-carbon economy”，as a new term of the 21st century，is related to the economic，political，technological，environmental protection and other areas．The game around the“Low-carbon economy”is complicated and the formation of interest groups is inevitable．However，common interests’existence makes the cooperation necessary．How to set up a reliable framework for cooperation has respect to our living environment，sustainable development and fair voice in the internationalmarket．Considering the factors about developing“low-carbon economy”，extracting the key factors to set up the gamemodel，using the static game and evolutionary game to analyze the developed countries and developing countries’conflicting interests in developing the low-carbon economy，may we finally get the stable equilibrium points that converge to，and we can find the conclusion that only by cooperation can the developed countries and developing countries achieve the best outcome of the game．At the same time，the result of the game proves that effective legal framework is the base of the cooperation to avoid the“hitch-hiker”．Finally all these may be revelations to China’s efforts in developing low-carbon economy．

low-carbon economy；developed countries；developing countries；nash equilibrium；evolutionary game

F205

A

1006-6152（2014）05-0005-08

2014－05－29本 刊 网 址·在 线 期 刊 ：http：／／qks．jhun．edu．cn／jhxs

樊 元，男，甘肃金昌人，西北师范大学经济学院教授；周 巍，男，湖北孝感人，西北师范大学经济学院硕士生。