起伏地表条件下频率-空间域声波介质正演模拟
郭振波,李振春
中国石油大学(华东)地球科学与技术学院,山东 青岛 266580
起伏地表条件下频率-空间域声波介质正演模拟
郭振波,李振春
中国石油大学(华东)地球科学与技术学院,山东 青岛 266580
频率-空间域正演模拟是频率域及Laplace-Fourier域全波形反演的基础,起伏地表条件下波形反演算法的关键是正演算法中考虑起伏地表的影响。基于带PML吸收边界的声波波动方程,在已有最优9点有限差分正演算法的基础上构建了起伏地表条件下频率-空间域正演算法。通过应用变网格技术,进一步提高算法的计算效率、降低内存开销,使得大规模起伏地表模型的频率域正反演问题成为可能。理论分析及数值测试表明:通过对近地表区域进行局部网格加密,可有效地压制由于矩形网格离散引起的角点散射;结合变网格技术可较易获得5倍以上计算效率的提高及内存占用的降低,且随着模型尺度的增加及地表起伏高程差的减小,倍数将显著增加;在细网格与粗网格交界处产生的虚假反射振幅幅值控制在原始波场的2%以内,满足地震波场正反演的需求。
起伏地表;变网格;频率域;数值正演
0 引言
随着计算能力的提高及对勘探目标刻画精度要求的提高,全波形反演正逐步成为一种高精度成像工具。全波形反演基于原始的双程波动方程,且能够同时考虑地震数据的各种波形信息,因此,该方法能够同时对模型的各个波数成分进行成像,成像精度较高。目前主要的波形反演方法集中在时间域、频率域、Laplace-Fourier域、Laplace域等,其中频率域与Laplace-Fourier域算法由于具有计算效率较高、较易实现多尺度反演、更容易估算震源子波等优势,在科学研究及实际应用中受到更多的关注[1-3]。高精度的频率-空间域正演算法是频率域与Laplace-Fourier域波形反演算法的基础,正演算法的效率及精度将直接影响反演的结果。目前主要的频率域正反演算法大都基于水平地表,且较少考虑自由边界,在处理实际资料时所用算法受到限制。波形反演算法能否直接处理起伏地表条件下采集数据的关键是所用正演算法是否考虑起伏地表的影响,因此,考虑起伏地表的频率域正演算法对于频率域与Laplace-Fourier域波形反演具有重要意义。此外,频率域正演算法与时间域算法相比数值实现及理论分析存在较大差异,同时还具有更易引入介质的黏滞性效应、对于多源正演效率较高、PML(完全匹配层)类吸收边界更易处理等优势。因此,考虑起伏地表的频率域正演算法在继承这些优势的同时可对起伏地表模型进行直接数值模拟,充分发挥正演算法的优势。综上所述,考虑起伏地表的高精度频率-空间域正演算法的研究不管是对于正演算法本身,还是随后的全波形反演方法都具有重要意义。
考虑起伏地表的正演方法较多,但各有优缺点。在处理起伏地表的正演方法中,可大致分为基于不规则网格的正演方法和基于规则网格的正演方法2类。基于不规则网格的正演方法为当前研究热点,主要包括有限元法(谱元法[4]、间断Galerkin法[5]等)、有限体积法[6]、基于曲网格[7-9]或非规则网格[10-11]的有限差分法等。对于有限元和有限体积类方法,由于求解波动方程的弱形式解能够自动满足自由边界条件,所以此类方法计算精度较高,但计算量一般较大;对于有限差分类方法,自由边界条件需要显示设置,计算精度相对于有限元类方法较低,但计算效率较高。基于不规则网格的正演方法严重依赖网格剖分的精度,由于速度模型在反演过程中不断更新,若没有一种有效的、实时的网格剖分方法,该类方法很难有效地应用到波形反演算法中。相对而言,基于规则网格的正演方法较易移植到波形反演算法中。然而,利用规则矩形网格并不能有效地描述起伏地表,阶梯状离散易产生角点散射。Jih等[12]通过将起伏地表进行折线近似来压制角点散射,但该方法较难扩展到三维;随后Robertsson等[13]提出了通过在近地表区域加密网格来压制角点散射,Hayshi等[14]、Wang等[15]对该方法进行了发展。虽然起伏地表条件下的正演算法较多,但是大都在时间域实现,频率域中算法很少。
在频率-空间域正演方法方面,研究重点大都集中在差分精度的提高上。Jo等[16]结合常规网格与旋转网格各自的优势,利用最小平方的思想求取了频率-空间域最优9点格式的差分系数;随后tekl等[17]将其推广到弹性介质正演;Shin等[18]发展了25点格式的频域正演算法;Hustedt等[19]详细分析并对比了最优9点格式与四阶差分格式;最近,曹书红等[20]推导了声波介质17点格式正演算法;吴国忱、梁锴等[21-22]推导并实现了TTI介质、VTI介质中频率正演的相关算法;韩立等[23]讨论了频率域正演中PML边界加载方法及频率域变网格步长计算策略。在频率域起伏地表处理方面,Brossier等[24]利用有限体积法对起伏地表条件下弹性波进行正演模拟,并随后将其应用到波形反演中。目前在频率域有限差分正演模拟中,关于起伏地表的研究较少。
笔者沿用经典的最优9点格式有限差分算法,在处理起伏地表时将时域算法中变网格的思想应用到频率域正演中;在近地表区域对网格进行加密处理,而其余部分应用常规粗网格,在保证正演精度的前提下提高了计算效率、降低了内存开销。除自由边界外,其余边界均采用PML类吸收边界条件。笔者首先概述最优9点格式频率-空间域正演算法的基本原理,然后给出起伏地表条件下自由边界条件及变网格技术的数值实现方法,最后通过数值实例证明方法的精度及对效率提高方面的优势。
1 频率-空间域最优9点格式有限差分正演模拟
频率-空间域带PML边界条件的二维声波波动方程为
(1)
其中:p为波场;ρ为密度;K为体积模量;f为震源项;s为PML吸收边界相关参数;下角x、z分别表示x轴与z轴。s的表达式为
(2)
其中:ω为角频率;d为吸收因子,主要影响PML层内波场振幅的衰减;α为频移因子,主要影响低频波的吸收;β为尺度因子,主要影响边界大角度入射波的吸收。当s=1时,没有吸收效应,波动方程退化为原始波动方程;当β=1、α=0时,吸收边界退化为常规PML边界条件;当β>1、α>0时,为CFS-PML(复频移完全匹配层)边界条件。根据不同的情况与要求,可对相应参数进行人为调整[25-26]。由于PML类吸收边界条件的定义及相关理论推导是在频率域给出的,所以相对于时域正演算法,在频率域实现更为简单。
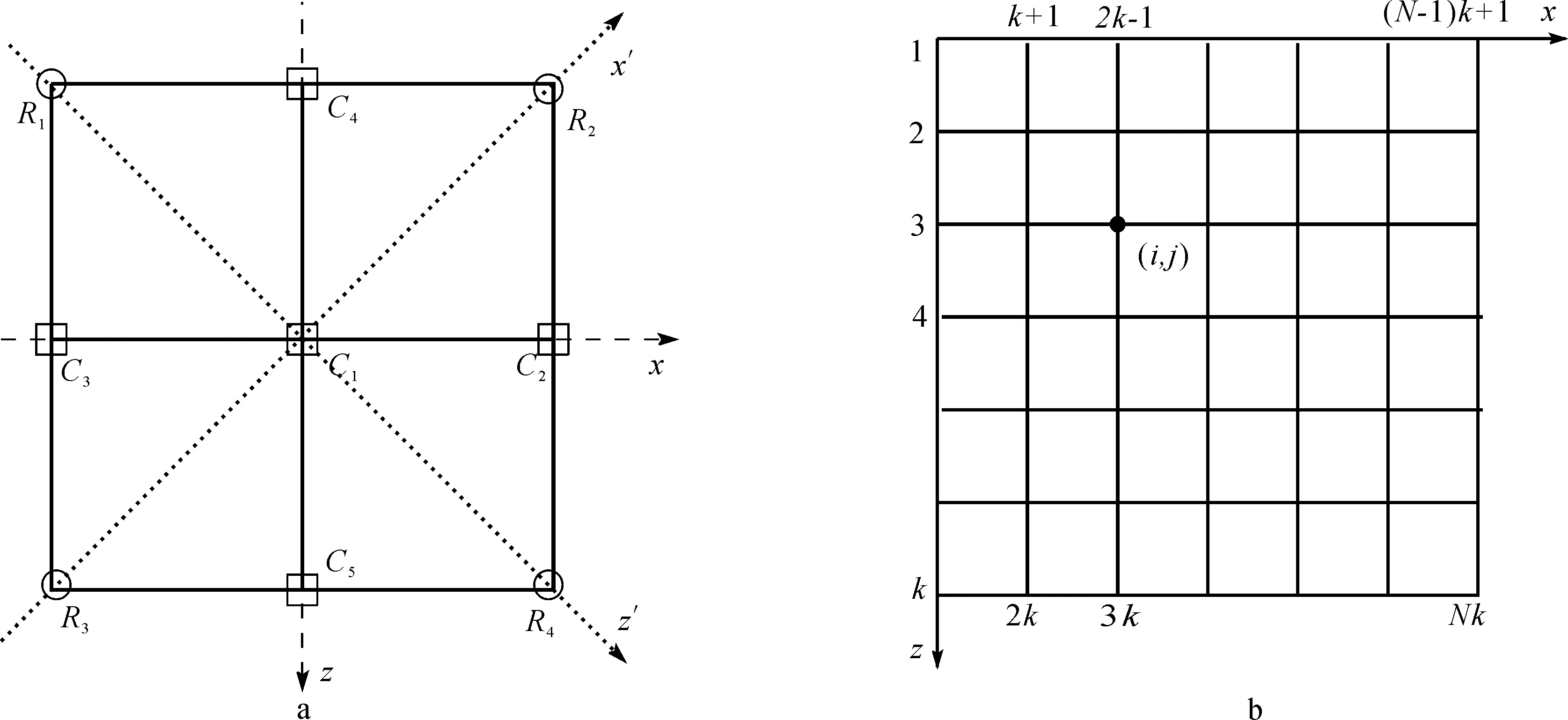
图1 常规最优9点差分格式(a)与网格离散方式(b)Fig. 1 Conventional optimal 9-point finite difference scheme (a) and discrete scheme (b)
在常规坐标系(图1a中x-z坐标系)中,有限差分数值频散在波传播方向与x(或z)轴夹角为0°时最大、45°时最小,而在旋转坐标系(图1a中x′-z′坐标系)中,数值频散在夹角为0°时最小、45°时最大。最优9点差分格式充分利用2种坐标系下数值频散的互补性,通过将2种坐标系下的空间求导项进行加权平均以减弱数值频散的各向异性;然后借鉴频率域有限元方法中将质量加速度项也用周围几个点加权平均表示的方法来提高正演的精度;最后利用最优化方法求取涉及到的加权系数以构建高精度频率域正演算法。详细的推导及分析可见参考文献[16,19]。
将波场及介质参数进行空间离散,并用最优9点差分格式代替空间求导项,可得原始波动方程的离散形式:
(3)
其中:pi,j为波场在离散网格点(i,j)上的波场值,如图1b所示;Ci与Ri为由介质参数、频率、差分系数、PML层参数、网格间距等共同控制的在相应点的加权系数;fi,j为震源项。与时域算法不同,在数值求解的过程中需要将笛卡尔坐标系下介质参数与波场映射到线性坐标系下以便将其写成向量的形式,如图1b中数字编号所示。此时,离散后的波动方程可以整理成矩阵的形式:

(4)
其中:A为阻抗矩阵;P为波场向量;F为震源项向量。
通过空间离散及有限差分近似,将原始偏微分方程的求解问题转化成为一稀疏线性方程组的求解问题。若模型离散后总点数为M,则P为大小为M×1的向量,A为大小为M×M的矩阵。式(4)可以通过直接法与迭代法2种方法求解,不管哪种方法,计算效率都随M的增加而显著增加。利用直接法求解时需要显示求取矩阵A的逆。虽然矩阵A是稀疏的,可压缩存储,但是矩阵A的逆并不一定是稀疏的,其大小与模型离散后总点数的平方成正比。在模型较大时,利用直接解法内存存储将是一个主要问题。综上所述,频率域正演算法的计算效率与模型离散后的总点数M有直接关系。在差分算法一定的情况下,提高频率域正演的计算效率、较低内存开销的最直接途径就是减少模型离散后的总点数。笔者借助MUMPS软件包进行稀疏线性方程组的求解[27]。
2 起伏地表条件下自由地表边界条件及变网格技术的引入
对于声波介质,在自由地表需满足应力为0的边界条件。在水平地表情况下,由于矩形网格与地表一致,较易处理自由边界;当地表起伏时,由于矩形网格并不能完整地描述起伏地表,阶梯状的离散方式易在正演波场中产生角点散射。当网格间距相对于地震波波长足够小时,角点散射可得到有效压制。研究表明,当一个波长内有15个以上采样时,角点散射才能得到有效压制[13]。本节首先概述起伏地表条件下频率域正演自由地表边界条件的加载方式,然后引入变网格技术,只对近地表附近网格进行加密处理,提高算法的计算效率并降低内存开销。
2.1 起伏地表条件下频率-空间域自由地表边界条件数值实现
虽然最优9点有限差分算法的推导是以一阶速度-应力方程为基础,并在数值离散的过程中用到了交错网格的相关算法,但是频域正演的最终形式是同位网格的形式。相对于交错网格算法,该方法加入自由边界较为容易;但相对于时域算法,在频域正演中自由边界条件的引入是隐式的,算法复杂性相对更高。
以图2中黄色方框所示区域为例进行分析。图2中绿色实线为地表实际位置,蓝色阶梯状实线为利用矩形网格对地表进行离散后的结果。考虑粗网格情况,若求取A点的空间导数需要用到B-I周围8个点的信息,由于E、F点位于自由表面以上,此处波场值为0。由于频率域正演最终的形式是求取式(4)所示的线性方程组,波场向量P中均为未知量;因此,首先需要将E、F点从波场向量中去除。同时结合式(3)可知,E、F点波场值为0等价于在差分时不考虑该点的影响,也就是说,在构建波场向量P及阻抗矩阵A时不考虑自由表面以上的点。在实际处理过程中,需要重新定义笛卡尔坐标系与线性坐标系之间的映射关系,并需做好自由表面以上网格点的识别。
对比图1b与图2左侧数字编号可知,在起伏地表条件下笛卡尔坐标系与线性坐标系的映射关系不能利用简单的函数关系表示,需要提前建立两者之间完整的映射关系。自由表面以上网格点的识别在笛卡尔坐标系中实现。
2.2 变网格技术及数值实现
利用矩形网格对起伏地表进行阶梯状空间离散,在正演过程中会因为阶梯状离散产生严重的角点散射。这是矩形网格处理起伏地表的共同问题,但角点散射会随着网格间距的减小而减弱。如图2所示,绿色曲线为实际地表高程,蓝色阶梯状曲线为利用粗网格离散后的结果,红色阶梯状曲线为利用细网格离散后的结果。通过对比可以看到,利用细网格离散后的结果不仅更接近真实地表形态,而且阶梯状幅度更小,将产生更少的虚假绕射波。
由前述可知,频率域正演的计算效率、内存开销与总共的网格点数有直接关系,全局细网格的正演算法在实际应用中无法接受。引入变网格技术,只在近地表区域加密网格,可在较精确模拟近地表效应的同时提高计算效率、降低内存开销。
变网格离散策略如图2所示。由于最优9点格式有限差分方法计算时需要周围一个网格间距内网格点上的波场值,细网格与粗网格的交界需要定义在地表最小高程一个粗网格间距以下的位置。在粗网格与细网格区域分别利用各自的网格间距进行求解。在过渡区域,粗网格中空间求导要用到该网格点上方网格的波场值,该波场值可直接从细网格中对应位置处取出;细网格中空间求导要用到该网格下方网格点的波场值,而该波场值大部分在粗网格中并没有定义,需利用粗网格点上波场值插值得到,如图2中空心圆圈所示。

图2 起伏地表条件下基于变网格的网格离散策略Fig. 2 Strategy of grid discretization based on variable grid when consider irregular topography
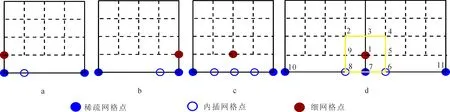
细网格点分别位于左边界(a)、右边界(b)、粗网格内部(c)、内部粗网格上(d)。图3 4种网格点内插示意图Fig. 3 Four different situations for grid interpolation
由于在粗网格上内插得到的点并未在阻抗矩阵中显式表示,而是隐式地表示为对应粗网格点上的权系数,所以需要考虑不同的情况分别进行处理。对于如图2所示的变网格离散策略,网格点内插时共有如图3所示的4种情况。当细网格点在左右边界及粗网格内部时,共需要粗网格2个网格点的值(图3a-c);当细网格在x方向与粗网格重合且不在左右边界上时,共需要3个粗网格点上的值(图3d)。具体实现方式以图3d中情况为例进行说明。对于图3d中标号为1的网格点,构建阻抗时需要其本身的值及周围8个点的信息。由于标号为7的网格点与粗网格点重合,所以只有标号为6和8的网格点需要通过粗网格上的值插值得到。假设其插值用下式表示:
(5)
其中:w1、w2、w3、w4为插值权系数。将式(5)带入式(3)可得到该情况下过渡区域的有限差分格式:
C1p1+C2p5+C3p9+C4p3+
(C5+R3w2+R4w3)p7+
(6)
笔者利用线性插值对缺失网格点进行波场插值,该方法使得在网格过渡区域产生的虚假反射控制在真实波场的2%以内,满足波形反演的需求。通过应用更适当的插值方法可进一步提高正演的精度。此外,变网格技术引入以后,笛卡尔坐标系与线性坐标系之间的映射关系将更为复杂,进一步增加了程序的复杂性。
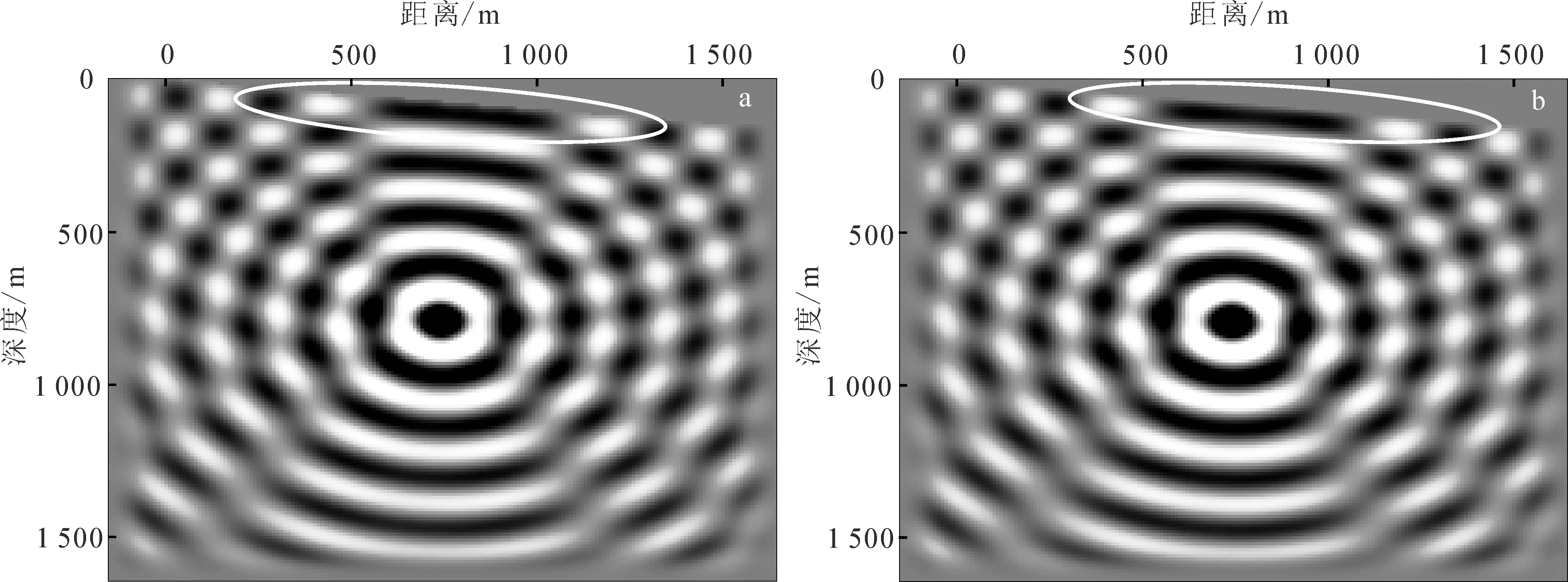
a. 常规网格; b. 变网格。图5 15 Hz频域波场的实部Fig. 5 Real part of wavefield in frequency domain at 15 Hz
3 模型试算
3.1 均匀介质模型

图4 均匀速度模型Fig. 4 Homogeneous velocity model
如图4所示,设计速度为2 500 m/s的均匀介质模型,网格采样间隔为10 m,纵横向采样点数均为150个。地表为一倾斜界面,高程由左到右逐渐减小,最大高差为149 m。震源位于模型中心位置,震源子波为15 Hz的雷克子波,检波器位于地表以下30 m。正演共用80个频率,频率采样率为0.5 Hz,除自由地表外其余3个边界均应用PML边界条件,PML层厚度为15个网格点。
除在原始网格上进行频域正演外,还利用基于变网格技术的正演算法进行正演模拟,如图4所示。加密网格的厚度为500 m,细网格间距为2 m,相应的加密倍数为5倍。正演所用其他参数与原始网格正演一致。
图5a、b分别为应用常规网格与变网格方法得到的15 Hz波场的实部。通过对比可知,2种网格正演波场基本一致,只是在自由表面处有明显差异。由于频率域波场对应震源子波为正弦波的时域波场,在频率域波场上较难进行波场的对比,故在随后的分析中将频率域波场变换到时间域进行分析。
0.316 s时刻的波场快照如图6所示。对比图6a与b可知,2种方法所得波场基本相同,细网格与粗网格边界处产生的虚假反射在图6b中完全看不到。将2种波场做差后的结果如图6c所示。从振幅幅值对比上可知,虚假反射的振幅小于原始波场的2%,远小于原始波场的振幅。从波形上分析可知,图6c中波场快照的差剖面主要由两部分构成,其中:标号①所示部分,即能量较强的部分为细网格与粗网格交界处的虚假反射;标号②所示部分,即能量较弱但分布范围较广的波场残差是由自由边界引起的,虽然直达波还未到达自由边界,但是由于傅里叶变换的周期性,图中波场残差为较大时刻的波场残差。通过两者的定量对比分析可知,本文所述方法与其他变网格方法一样,虽然在细网格与粗网格交界处产生虚假反射,但是相对于原始波场能量较弱,在波场的正反演中可以接受。

a. 常规网格正演结果;b. 变网格正演结果;c. 两者之差。图6 0.316 s时刻波场快照对比Fig. 6 Comparison of wavefield snaps at 0.316 s

0.48 s时刻波场快照:a. 常规网格;b. 变网格。0.62 s时刻波场快照:c. 常规网格;d. 变网格。图7 不同时刻波场快照对比Fig. 7 Comparison of wavefield snaps at different time
图7为2个较大时刻波场快照对比图。由图7a与b可知,引入变网格技术并没有改变PML边界吸收的效果,也没有因为网格变化产生不稳定(白色虚框所示区域)。同时,从图7a与b中可以看到PML吸收边界良好的吸收效果。对于起伏情况下自由边界的处理效果,在图7c与d中可以更明显地看到。在图7c中由于粗网格对起伏地表的阶梯状离散更为明显,产生严重的角点散射(箭头所指区域)。通过在近地表区域加密网格,有效地压制了角点散射,如图7d所示。在图8所示的炮记录上,也可以明显地看到变网格技术的引入对角点散射的压制。
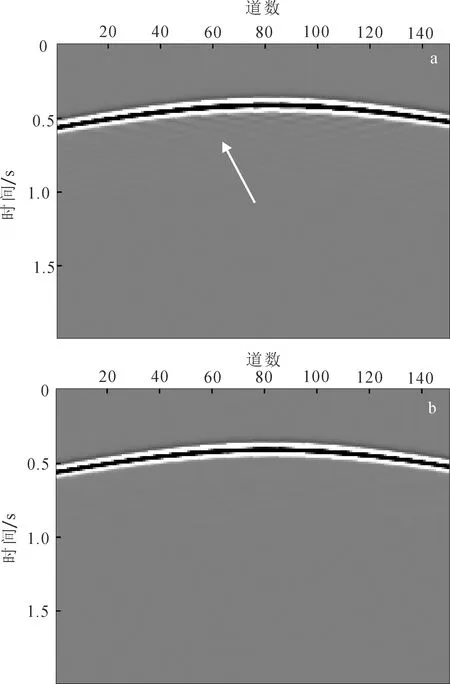
a. 基于常规网格正演方法;b. 基于变网格正演方法。图8 炮集对比Fig. 8 Comparison of shot gathers
3.2 复杂介质模型
通过对复杂介质模型进行数值测试验证本文所述方法对模型复杂性的适应性,同时定量分析变网格方法的引入对效率提高等方面的优势。
所用模型如图9所示,横向与纵向范围均为2 400 m,速度为2 500~3 800 m/s。模型中既有大尺度的背斜、断层等构造,也有小尺度的绕射点,可测试算法对复杂模型的适应性。起伏地表左侧设计为连续变化的类正弦状起伏,右侧为不连续变化的折线状起伏,可测试算法对不同起伏情况的适应性。绘图时将起伏地表以上利用速度为1 500 m/s的均匀介质填充以获取较好的图形显示效果。为对比算法的计算效率与精度,常规网格选取间距为4 m的细网格,横纵向均为600个采样点。震源位于横向1 400 m、地表以下40 m处,正演所用子波为主频、为15 Hz的雷克子波,共用到110个频率,频率采样间隔为0.416 67 Hz。PML吸收层厚度为20个采样点。在基于变网格的正演方法中,粗网格处网格间距为12 m,表层加密后的网格间距为4 m,加密网格厚度为576 m,其他正演参数与细网格下正演参数一致。
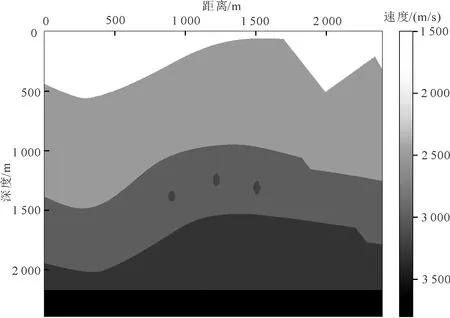
图9 复杂介质模型Fig. 9 Complex velocity model

0.418 s时刻波场快照:a. 细网格;b. 变网格;c. 两者之差。0.837 s时刻波场快照:d. 细网格;e. 变网格;f. 两者之差。图10 不同时刻波场快照对比Fig. 10 Comparison of wavefield snaps at different time
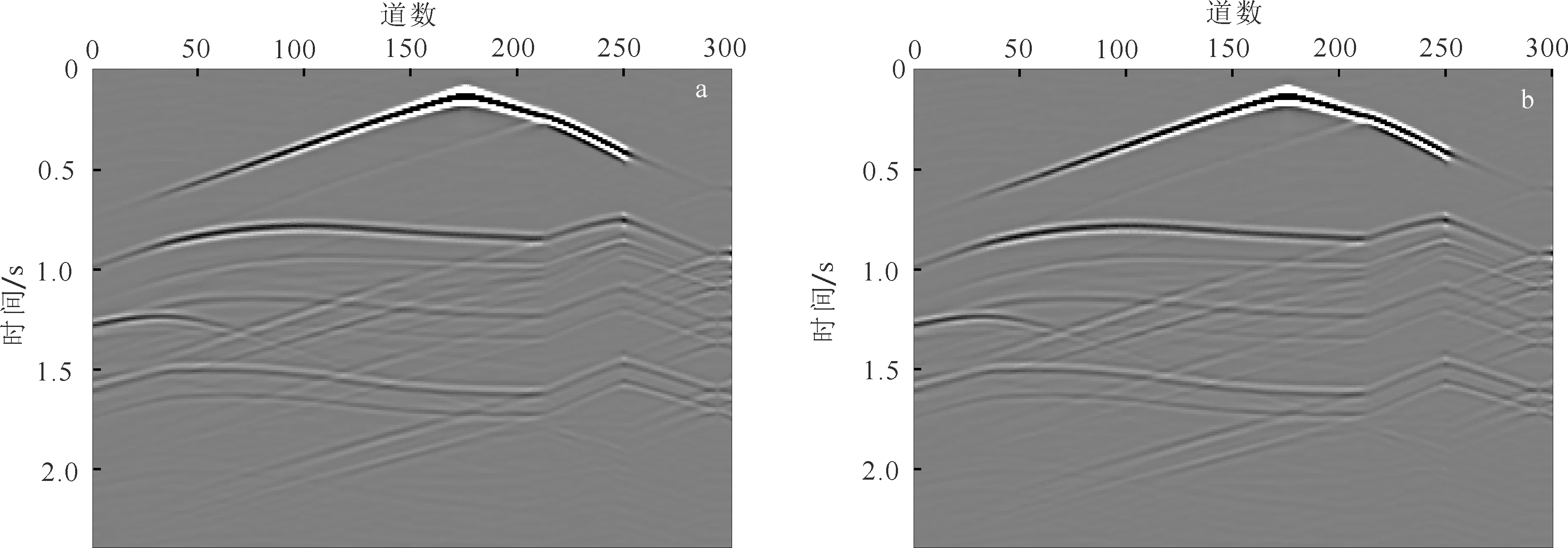
a. 常规方法在细网格下正演记录;b. 本文所述方法所得正演记录。图11 炮集对比Fig. 11 Comparison of shot gather
利用2种方法所得不同时刻波场快照如图10所示。图10a与d分别为0.418 s与0.837 s时刻的波场快照,在波场快照上可以较清晰地看到起伏地表对波场的影响。标号②处为直达波与虚反射的叠加;由于震源距离地表较近,两者在旅行时上差异较少以致在波形上很难分开。标号①处为在右侧高角度起伏地表产生的反射波;该类型波使得随后的波场传播过程更为复杂,这也在一定程度上说明了考虑起伏地表的重要性。标号③处为地下第一个界面反射波在自由地表产生的表层多次波。通过波场分析可知,由于起伏地表的影响使得地下波场更为复杂,这种波场的复杂性在接收记录上也可以清晰地看到,如图11所示。由于地表的起伏主要反射轴已不完全是双曲形态,给波场的分析带来很大困难,这也在一定程度上验证了在反问题中考虑起伏地表的重要性。
分别对比分析图10a与b及图10c与d中波场快照可知:基于变网格的正演方法与基于细网格的常规方法具有相同的精度,并没有因为网格的变化而引起波场不稳定等问题;同时细网格与粗网格交界处的虚假反射由于能量相对很弱,在波场快照中基本看不到其存在。图10c与f分别为2个时刻波场快照在2种方法下的波场差异。对比分析图10a-c可以看到:由于地震波还没有传播到地下反射层,波场残差主要是细网格与粗网格交界处产生的虚假反射(图中白色箭头所示),虚假反射波振幅是原始波场的0.5%,对波场影响较小。与图10c不同,图10f由于是较大时刻的波场残差,其中除了细网格与粗网格交界处的虚假反射外,更多的是由于576 m以下粗网格区域与细网格对介质参数的离散采样不同引起的,这是有限差分方法共同的问题。然而通过能量对比可以看到,即使波场残差较为复杂,但是整体能量相对原始波场较弱,在实际波场的正演与反演过程中是可以接受的。图11为2种方法的观测记录。两者波场基本一致,在图11b上基本看不到由网格变化引起的虚假反射。
本模型试算所用程序利用Fortran语言编写,程序在Linux操作系统下利用ifort编译,编译时未加优化选项,运算CPU主频为2.4 GHz的Intel双核处理器(型号为E6600),运算时只用单线程。基于细网格的常规方法共用时15 min 31 s,内存占用在500 MB左右;而基于变网格的方法用时2 min 36 s,内存占用在90 MB左右。可以看到,通过引入变网格技术,计算效率提高了6倍以上,内存占用降低到原先的1/5以内。当所用模型横纵向范围进一步变大时或起伏地表高程差进一步缩小时,在内存占用及计算效率等方面的优势将更明显。
4 结论
笔者建立并数值实现了频率-空间域起伏地表条件下的数值正演算法,通过将时域正演中的变网格技术应用到频域正演,有效地提高了计算效率、减少了内存开销。数值试验证明由网格间距变化引起的虚假反射波振幅幅值控制在原始波场的2%以内,满足波场正反演的要求;借助变网格技术可在保证精度的情况下较易得到5倍以上的加速比,且加速比随着模型尺度的增加或起伏地表高程差的减小而增加。此外对内存占用的大幅减少,使得对大尺度模型的频域正演成为可能。
通过加入起伏地表自由边界条件,进一步扩展了频域正演方法的应用范围,可充分发挥频率正演较易引入介质黏滞性、对多源正演效率较高、PML类吸收边界精度更高等优势。为了提高计算效率,时域算法在空间变网格的同时往往还需要进行局部时间变步长,而频域算法则不需要,相对而言减少了误差来源,正演精度更高。此外,本文所述正演方法为起伏地表下的频率域与Laplace-Fourier域波形反演奠定了坚实的基础。
本文在细网格与粗网格的过渡区域,通过线性插值对缺失网格点上的波场进行插值。虽然得到了可接受的插值精度,但并不是最优的方式;推导并应用更精确的插值方法以取得更高精度的波场将是随后的研究重点。
[1] Virieux J, Operto S. An Overview of Full-Waveform Inversion in Exploration Geophysics[J]. Geophysics, 2009,74(6):1-26.
[2] Pratt R G. Seismic Waveform Inversion in the Frequency Domain:Part 1: Theory and Verification in a Physical Scale Model[J]. Geophysics, 1999, 64(3): 888-901.
[3] Shin C, Cha Y H. Waveform Inversion in the Laplace-Fourier Domain[J]. Geophys J Int, 2009, 177(3): 1067-1079.
[4] Komatitsch D, Tromp J. Introduction to the Spectral-Element Method for 3D Seismic Wave Propagation[J]. Geophys J Int, 1999, 139(3):806-822.
[5] Käser M, Dumbser M. An Arbitrary High-Order Discontinuous Galerkin Method for Elastic Waves on Unstructured Meshes: I: The Two-Dimensional Isotropic Case with External Source Terms[J]. Geophys J Int, 2006, 166(2): 855-877.
[6] Dumbser M, Käser M, Puente J D L. Arbitrary High-Order Finite Volume Schemes for Seismic Wave Propagation on Unstructured Meshes in 2D and 3D[J]. Geophys J Int, 2007, 171(2):665-694.
[7] Tessmer E, Kosloff D, Behle A. Elastic Wave Propagation Simulation in the Presence of Surface Topography[J]. Geophys J Int, 1992,108(2):621-632.
[8] Wang X C, Liu X W. 3-D Acoustic Wave Equation Forward Modeling with Topography[J]. Applied Geophysics, 2007, 4(1):8-15.
[9] 丘磊. 正交曲线坐标系下的地震波数值模拟技术研究[D]. 杭州:浙江大学,2011. Qiu Lei. Study on Seismic Wave Simulations in Orthogonally Curvilinear Coordinate System[D]. Hangzhou: Zhejiang University, 2011.
[10] 张剑锋. 弹性波数值模拟的非规则网格差分法[J]. 地球物理学报,1998,41(增刊1):357-366. Zhang Jianfeng. Non-Orthogonal Grid Finite-Diffe-rence Method for Numerical Simulation of Elastic Wave Propagation[J]. Acta Geophysica Sinica, 1998, 41(Sup.1): 357-366.
[11] Käser M, Igel H. Numerical Simulation of 2D Wave Propagation on Unstructured Grids Using Explicit Differential Operators[J]. Geophysical Prospecting, 2001, 49(5) :607-619.
[12] Jih R, McLaughlin K L, Der Z A. Free-Boundary Conditions of Arbitrary Polygonal Topography in a Two-Dimensional Explicit Elastic Finite-Difference Scheme[J]. Geophysics, 1988, 53(8):1045-1055.
[13] Robertsson J O A, Holliger K. Modeling of Seismic Wave Propagation near the Earth’s Surface[J]. Physics of the Earth and Planetary Interiors, 1997, 104(1/2/3): 193-211.
[14] Hayashi K, Bruns D R, Toksöz M N. Discontinuous-Grid Finite-Difference Seismic Modeling Including Surface Topography[J]. Bulletin of the Seismological Society of America, 2001, 91(6): 1750-1764.
[15] Wang Y, Xu J, Schuster G. Viscoelastic Wave Simulation in Basin by a Variable-Grid Finite-Difference Method[J]. Bulletin of the Seismological Society of America, 2001, 91(6): 1741-1749.
[16] Jo C, Shin C, Suh J H. An Optimal 9-Point, Finite-Difference,Frequency-Space 2-D Scalar Wave Extra-polator[J]. Geophysics, 1996, 61(2):529-537.
[18] Shin C, Sohn H. A Frequency-Space 2-D Scalar Wave Extrapolator Using Extended 25-Point Finite-Difference Operator[J]. Geophysics, 1998, 63(1): 289-296.
[19] Hustedt B, Operto S, Virieux J. Mixed-Grid and Staggered-Grid Finite-Difference Methods for Frequency-Domain Acoustic Wave Modeling[J]. Geophys J Int, 2004, 157(3): 1269-1296.
[20] 曹书红,陈景波. 声波方程频率域高精度正演的17点格式及数值实现[J]. 地球物理学报, 2012,55(10):3440-3449. Cao Shuhong, Chen Jingbo. A 17-point Scheme and Its Numerical Implementation for High-Accuracy Modeling of Frequency-Domain Acoustic Equation[J]. Chinese Journal Geophysics, 2012,55(10): 3440-3449.
[21] 吴国忱,梁锴. VTI介质qP波方程高精度有限差分算子[J]. 地球物理学进展,2007, 22(3):896-904. Wu Guochen, Liang Kai. High Precision Finite Difference Operators for qP Wave Equation in VTI Media[J]. Progress in Geophysics, 2007, 22(3): 896-904.
[22] 梁锴,吴国忱,印兴耀. TTI介质qP波方程频率-空间域加权平均有限差分算子[J]. 石油地球物理勘探,2007,42(5):516-525. Liang Kai, Wu Guochen, Yin Xingyao. Weighted Mean Finite-Difference Operator of qP Wave Equation in Frequency-Space Domain for TTI Medium[J]. Oil Geophysical Prospecting, 2007, 42(5):516-525.
[23] 韩立,韩立国,李翔,等. 二阶声波方程频域PML边界条件及频域变网格步长并行计算[J]. 吉林大学学报:地球科学版,2011,41(4):1226-1232. Han Li, Han Liguo, Li Xiang, et al. PML Boundary Conditions for Second-Order Acoustic Wave Equations and Variable Grid Parallel Computation in Frequency-Domain Modeling[J]. Journal of Jilin University: Earth Science Edition, 2011, 41(4):1226-1232.
[24] Brossier R, Virieux J, Operto S. Parsimonious Finite-Volume Frequency-Domain Method for 2D P-SV Wave Modeling[J]. Geophy J Int, 2009, 175(2): 541-559.
[25] Pan G, Abubakar A, Habashy T M. An Effective Perfectly Matched Layer Design for Acoustic Fourth-Order Frequency-Domain Finite-Difference Scheme[J]. Geophys J Int, 2012, 188(1): 211-222.
[26] 田坤,黄建平,李振春, 等. 实现复频移完全匹配层吸收边界条件的递推卷积方法[J]. 吉林大学学报:地球科学版,2013,43(3):1022-1032. Tian Kun, Huang Jianping, Li Zhenchun, et al. Recursive Convolution Method for Implementing Complex Frequency-Shifted PML Absorbing Boundary Condition[J]. Journal of Jilin University: Earth Science Edition, 2013, 43(3):1022-1032.
[27] Amestoy P R, Duff I S, Koster J, et al. A Fully Asynchronous Multifrontal Solver Using Distributed Dynamic Scheduling[J]. SIAM Journal of Matrix Analysis and Applications, 2001, 23(1):15-41.
Acoustic Wave Modeling in Frequency-Spatial Domain with Surface Topography
Guo Zhenbo, Li Zhenchun
SchoolofGeosciences,ChinaUniversityofPetroleum(EastChina),Qingdao266580,Shandong,China
Seismic wave modeling in frequency-space domain is the foundation of full waveform inversion in frequency and Laplace-Fourier domain. An accurate seismic wave modeling with surface topography is the kernel of full waveform inversion which can direct process data recorded on relief surface. Based on acoustic wave equation with PML absorption boundary condition, the free surface condition on relief surface is included into the optimized 9-points finite difference algorithm in frequency space domain. Then the variable grid method which refines the grid near the surface and remains the rest unchangeable is introduced to increase the computational efficiency and decrease the memory cost. The theoretical analysis and numerical test show that: 1) the diffraction caused by grid discretization of the relief surface can be suppressed by refining the grid; 2) through the variable grid method, computational efficiency can be improved for several times and the memory cost can also be decreased for several times easily; 3) the energy of artificial reflection caused by the boundary of fine and coarse grid is less than 2% of the energy of the original wavefield which is acceptable for the seismic wavefield modeling and inversion.
surface topography; variable grid; frequency domain; numerical modeling
10.13278/j.cnki.jjuese.201402305.
2013-07-04
国家自然科学基金项目(40974073);国家“863”计划项目(2011AA060301);中央高校基本科研业务费专项资金(13CX06014A)
郭振波(1986-),男,博士研究生,主要从事地震波场正演模拟与波形反演等方面的研究,E-mail:stone_gzb@163.com。
10.13278/j.cnki.jjuese.201402305
P631.4
A
郭振波,李振春. 起伏地表条件下频率-空间域声波介质正演模拟.吉林大学学报:地球科学版,2014,44(2):683-693.
Guo Zhenbo, Li Zhenchun. Acoustic Wave Modeling in Frequency-Spatial Domain with Surface Topography.Journal of Jilin University:Earth Science Edition,2014,44(2):683-693.doi:10.13278/j.cnki.jjuese.201402305.

