入口温度对换热器污垢热阻的影响及其修正

曹生现 周 昊 张腾宇 李宗攀 时丕栋

(东北电力大学自动化工程学院，吉林 吉林 132012)

换热器是化工厂中重要的化工设备之一[1]，流经换热设备的循环冷却水会因温度和流速的变化在换热器壁面上逐渐形成污垢[2]，常常引起局部过热或超温导致机械性能下降，从而引发事故。结垢也常常引起换热面局部腐蚀乃至穿孔，严重威胁了换热设备的安全运行，而且造成了巨大的经济损失。当换热面上形成污垢后，流体与换热面之间的传热热阻就会增加，这种在污垢形成后增加的传热热阻为污垢热阻，它通常随运行条件和时间的变化而变化。

为测取不同条件下的污垢热阻，Howarth J H等描述了一种基于模拟换热器热平衡原理的过程监测器，提出了旨在用于新型装置设计和计算优化清洁周期的污垢监测技术[3]；徐品政和罗益民设计了一种基于C8051F021单片机的新型污垢热阻在线监测仪，在计算污垢热阻的同时还可以对监测系统的水流量和蒸汽温度进行PID控制[4]；王维珍等设计了海水冷却腐蚀热阻一体化监测装置，该装置主要由腐蚀测试、污垢热阻测量和微机管理监测系统3部分组成[5]。以上测量装置都能够监测污垢热阻并采集到污垢热阻的数据，但是没有精确计算入口温度对污垢热阻的影响，污垢热阻的测量结果不够准确，在一定工况下与实际值存在较大偏差。

笔者利用自制的循环冷却水污垢热阻在线监控装置[6]，研究了循环冷却水入口温度对污垢热阻的影响，并针对无垢和有垢两种情况，分别对污垢热阻监测模型进行修正，以减小入口温度对污垢热阻的影响，提高测量精度。

1 污垢热阻测量原理及其与入口温度的关系①

1.1 污垢热阻的测量原理

温差监测法是污垢热阻测量的常用方法，它通过换热器工艺介质和冷却水进、出口温差的变化来反映污垢沉积量的变化。这种监测方法方便、直观，其缺陷在于精度差，在不采用校正手段的情况下，它只能作为描述换热面污垢聚集的一个参考值。根据文献[7]中对温差监测法的定义，污垢热阻Rf的计算式为：

(1)

式中q——热流密度；

Ts——污垢表面温度；

Twf——界面温度。

1.2 污垢热阻与入口温度的关系

自制的污垢热阻监测装置中，Twf为换热器壁温值。由于金属材料的导热系数远大于污垢的导热系数，可认为换热器整个壁面温度Twf为常数，因此污垢热阻Rf只与污垢表面温度Ts和热流密度q有关，且成反比例关系。式(1)中的热流密度q的计算式为：

(2)

由于在本实验装置中管径d、流速V、定压比热容cp、密度ρ和管长l都是常数，因此热流密度q只与温差ΔT(ΔT=To-Ti)有关。而出口温度To相对稳定，所以热流密度q仅与入口温度Ti有关，即入口温度Ti增大，热流密度q减小。

式(1)中污垢表面温度Ts的计算式为：

(3)

由热平衡规律可知：

(4)

其中，循环冷却水温度Tf可以表示为：

(5)

由式(4)、(5)可得：

(6)

当入口温度Ti增大时，E减小，从而使1-E增大，联合式(3)可知Ts≈Ti，所以当入口温度Ti增大时污垢表面温度Ts也增大。

入口温度Ti增大导致热流密度q减小，污垢表面温度Ts增大，从而使污垢热阻Rf减小；反之，入口温度Ti减小会使污垢热阻Rf增大。因此，循环冷却水入口温度Ti与换热器污垢热阻Rf成反比例关系。

2 污垢热阻测量模型的修正

2.1 无垢时热阻测量模型修正

根据文献[7]污垢热阻法的另一种常用的测量方法表达形式为：

(7)

式中Uc——洁净状态下换热管的总换热系数；

Uf——带有污垢的换热管的总换热系数。

结合式(1) 、(7)可得洁净状态下的总传热热阻：

(8)

同理,可以得到有污垢状态下总传热热阻为：

(9)

由于洁净状态下Tsc=0，所以根据式(7)～(9)可得：

(10)

联立式(2)、(3)、(10)，整理可得污垢热阻测量模型的修正公式为：

(11)

自制污垢热阻监测装置中管径d、定压比热容cp、密度ρ和管长l都是常数，流速V、壁温和入口温度可测量，代入测量参数可得无垢时污垢热阻的修正公式为：

Rf=-0.0000011Ti+0.000358

(12)

2.2 有垢时热阻测量模型修正

有垢情况下，即污垢呈上升趋势并逐渐趋于稳定时，利用最小二乘法智能算法修正污垢热阻[8]。污垢热阻的监测数据满足原型函数y=alog2x+b，应用最小二乘法原理求出a和b。其中y为污垢热阻，x为数据采集时间次序。

令：

(13)

最小二乘法修正污垢热阻就是求出使M取得最小值时的a、b，如果把M看作是自变量a和b的函数，由多元函数取最值得条件可知：

(14)

求解得：

(15)

整理得：

(16)

y=alog2x+b

(17)

上述求解参数a和b的过程可在Matlab环境下直接使用polyfit函数实现，具体的命令格式为：

x=1,2,3,…,n

y=热阻1，热阻2，热阻3，…,热阻n

a=[0 0]

a=lsqcurvefit(@myfun,a0,x′,y)

y2=a(1,1)*logx+a(1,2)

其中lsqcurvefit表示的是最小二乘原理，a(1,1)是logx的系数，a(1,2)是常数项。综上所述，污垢热阻的修正公式为：

(18)

2.3 修正方法的选择

采用自制的污垢热阻在线监测装置，对于监测的污垢热阻数据，可采用无垢和有垢情况分别处理，修正算法的过程如图1所示。

图1 修正公式的计算过程

3 验证结果分析

为了检验修正公式的准确性，分别选取两组无垢和两组有垢数据按照图1所示方法进行验证。

3.1 无垢时热阻修正结果

图2中变化较大的污垢热阻数据是某热电厂运行的自制污垢热阻在线监控装置运行初期监测到的污垢热阻数据，即此时为无垢状态。根据修正公式Rf=-0.0000011T+0.000358对监测的污垢热阻数据进行修正，修正结果如图2所示。其中，数值变化较大曲线代表原始的污垢热阻数据，变化较小的曲线表示修正后的污垢热阻数据。

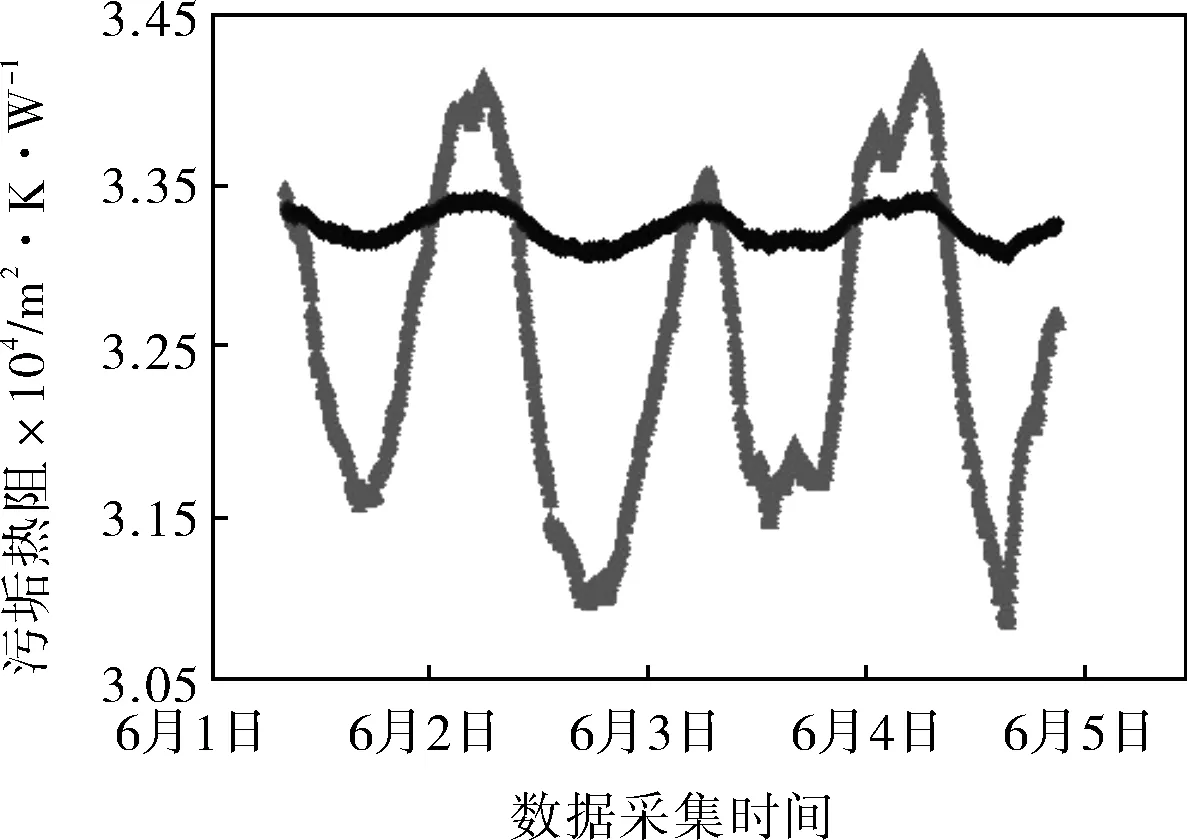
a. 第一组

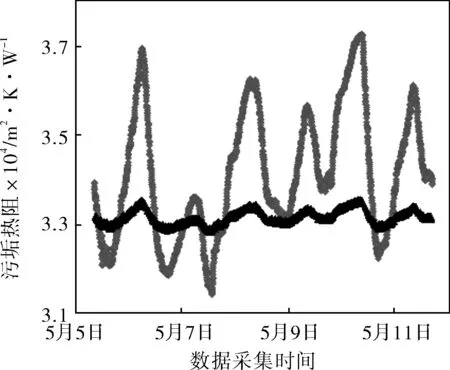
b. 第二组

由图2可以看出：污垢热阻原始数据的曲线热阻值变化较大，在换热器未结垢的状态下，污垢热阻值测量误差较大；经修正后，污垢热阻曲线的波动较为平稳，可准确反映换热器实际测量值，从而保证了监测数据的准确性。

3.2 有垢时热阻修正结果

图3中波动较大的数据为自制污垢监测装置在实验室模拟实验所获取的污垢热阻数据，由曲线变化趋势可知，此时换热器内已形成了污垢，即为有垢数据曲线。按照修正公式Rf=alog2x+b对污垢数据进行修正，修正公式的系数a和b可以根据所监测到的原始污垢热阻值计算得出，修正结果如图3所示。从图3中可以看出，修正后的污垢热阻数据，曲线较为平滑，污垢热阻的数值稳定，变化规律更加明显，表明了修正公式的有效性。

a. 第一组

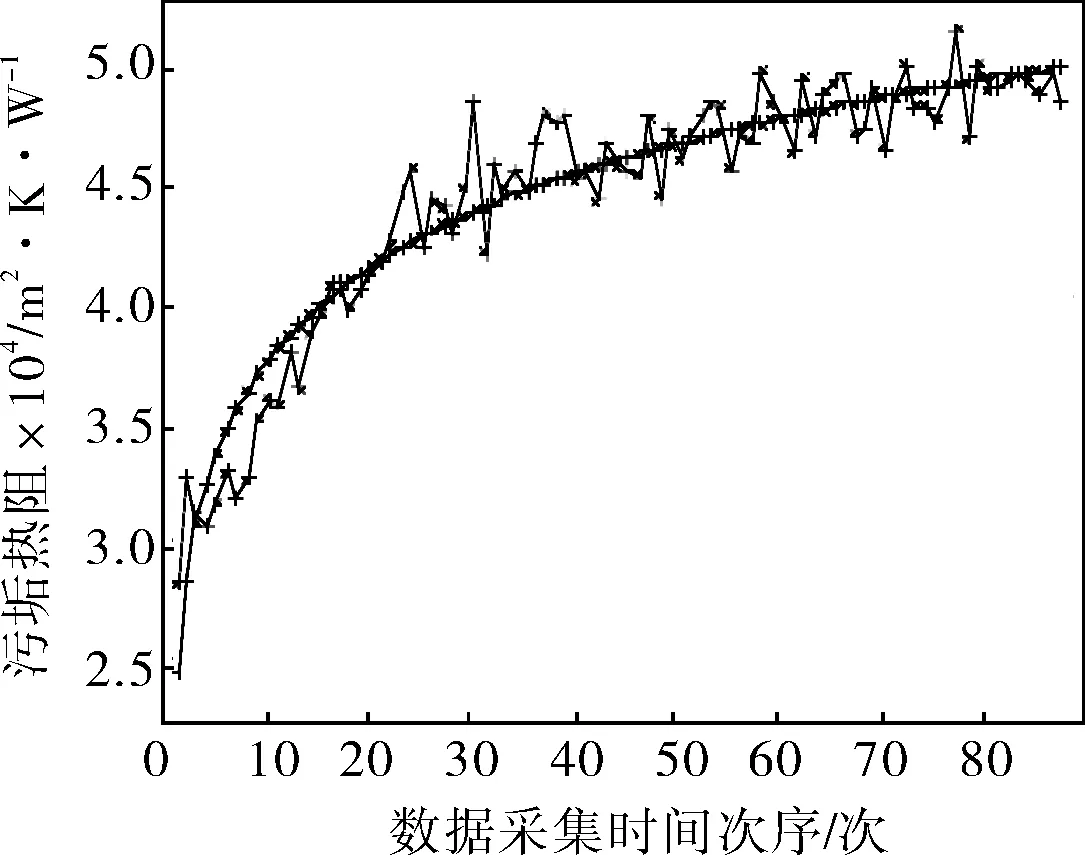
b. 第二组

4 结束语

通过对自制的污垢热阻在线监控装置获得数据分析，确定了入口温度与换热器污垢热阻呈反比的关系，并针对无垢和有垢两种情况，建立了换热器污垢热阻的修正模型。通过某电厂和实验室的污垢热阻数据处理，验证了污垢热阻修正模型的有效性，该修正模型不仅减小了入口温度对污垢热阻的影响，同时减小了污垢热阻的波动，提高了污垢热阻的测量精度。