基于改进型GPC算法的液位优化控制

吴燕翔 高中勇

(上海海洋大学工程学院，上海 201306)

随着化工行业的日益发展,化工生产的自动化程度越来越高,要真正实现无人控制,化工自动化是必不可少的环节[1]。在化工自动化中，最常见的控制问题是液位控制。化工生产的实际液位控制问题都可以简化为某种水箱的液位控制问题[2]。因此，液位是化工生产控制过程中一个重要的参数，特别是在动态状态下，采用合适的方法对液位进行监测、控制，能收到很好的操作效果[3]。

在化工生产中液位控制系统常用的是PID控制，经典的PID控制适用于单输入/单输出系统，对多输入/多输出非线性系统的效果很难达到人们的预期目标[4]。在这里，笔者引入广义预测控制(GPC)。以双容液位装置为被控对象，基于NetCon平台，利用MATLAB/Simulink程序开发工具，对广义预测控制进行仿真和实验研究。采用广义预测控制算法，通过比较，选取改进型GPC算法，即JGPC算法。通过仿真实例验证了这种算法在控制性能上的可行性和有效性。该算法提高了对非线性系统控制的稳定性，克服了双容水箱的容积延迟问题。

1 液位系统建模①

双容水箱在化工工业过程控制中应用非常广泛。在双容水箱水位的控制中,进水首先进入第一个水箱,然后通过第二个水箱流出,与一个水箱相比，由于增加了一个水箱，使得被控量的响应在时间上落后一步,即存在容积延迟,从而导致该过程难以控制。

在控制系统的分析和设计中，首先要建立系统的数学模型[5]。控制系统的数学模型是定量描述系统或过程内部物理量(或变量)之间关系的数学表达式[6]。利用辨识的方法建立系统的数学模型，首先根据系统辨识的目的，利用先验知识，初步确定模型结构；然后采集输入输出数据并进行相关处理，再进行模型结构辨识和模型参数辨识；最后经过验证获得最终模型。预测控制原理如图1所示。

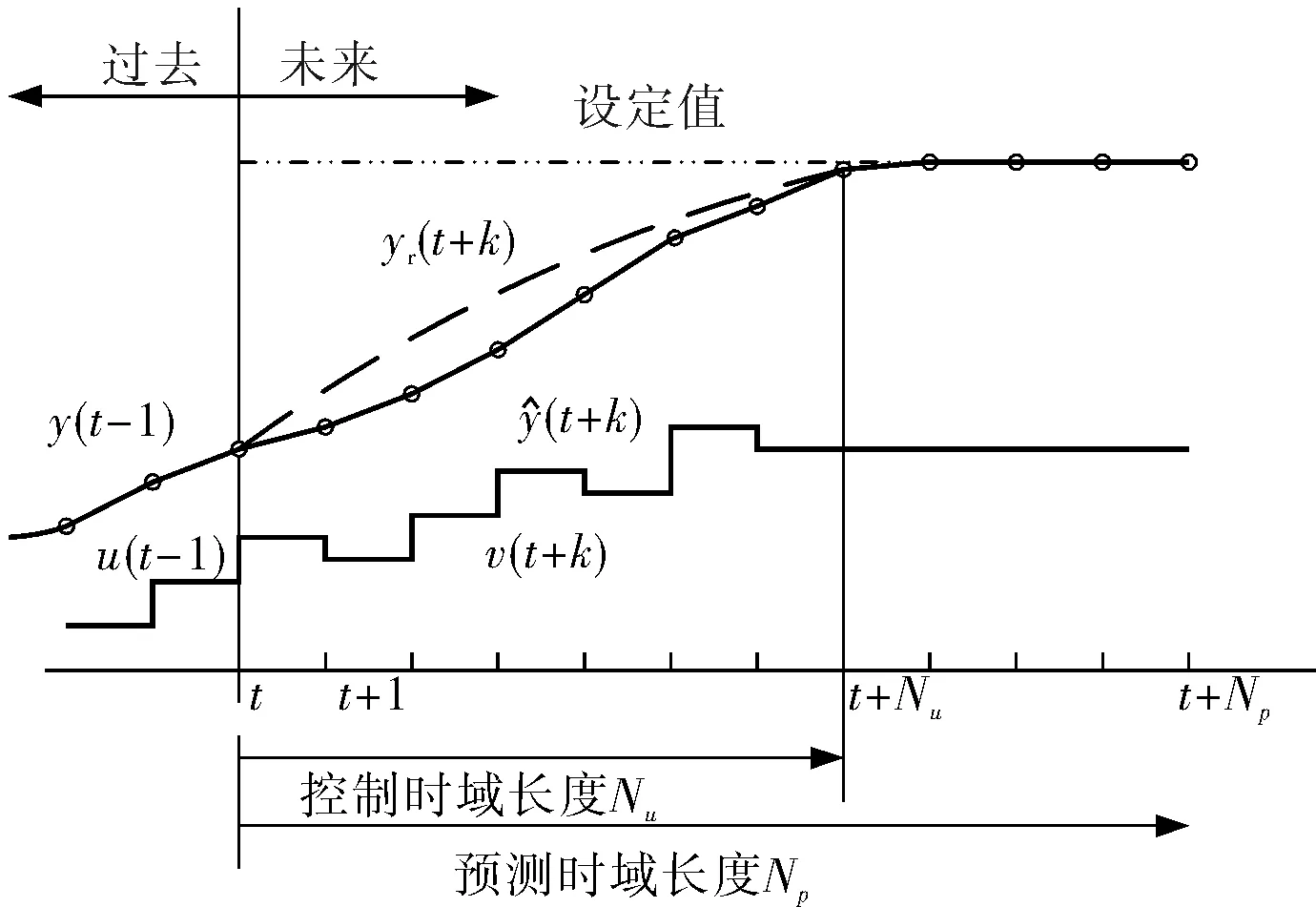
图1 预测控制原理

2 GPC算法的优化

2.1 GPC算法的比较

GPC算法中常用的是定常GPC算法、GPC自适应算法和改进后的GPC算法，即JGPC算法，这3种算法分别各有优缺点，为了适应所选系统，达到最好的控制效果，现进行GPC算法的选取。设被控对象为如下开环不稳定非最小相位系统：

y(k)-2y(k-1)+1.1y(k-2)=u(k-4)+2u(k-

5)+ε(k)/Δ

其中，ε(k)为方差为0.01的白噪声。

3种算法的仿真如图2～4所示。

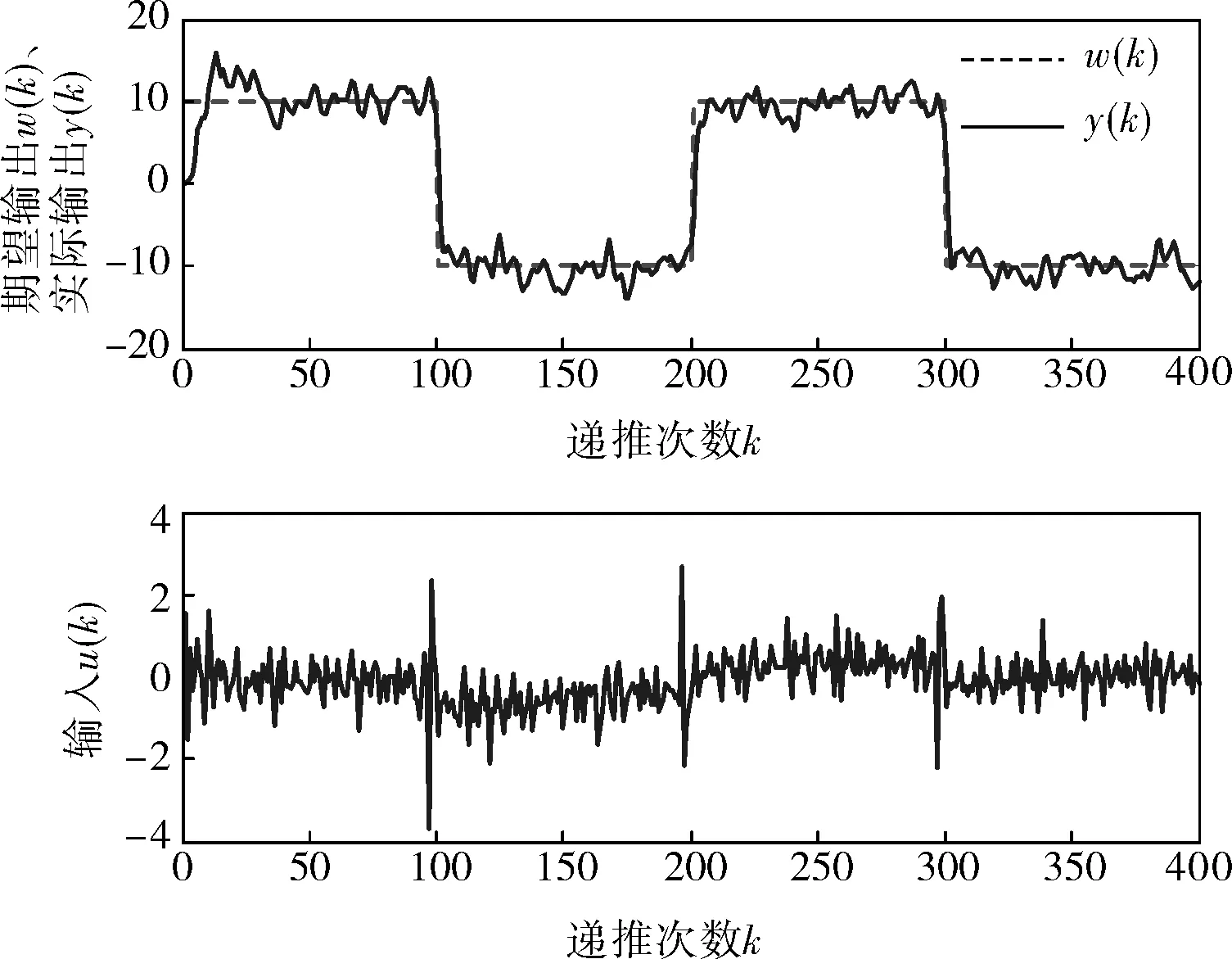
图2 定常GPC算法仿真

图3 GPC自适应算法仿真

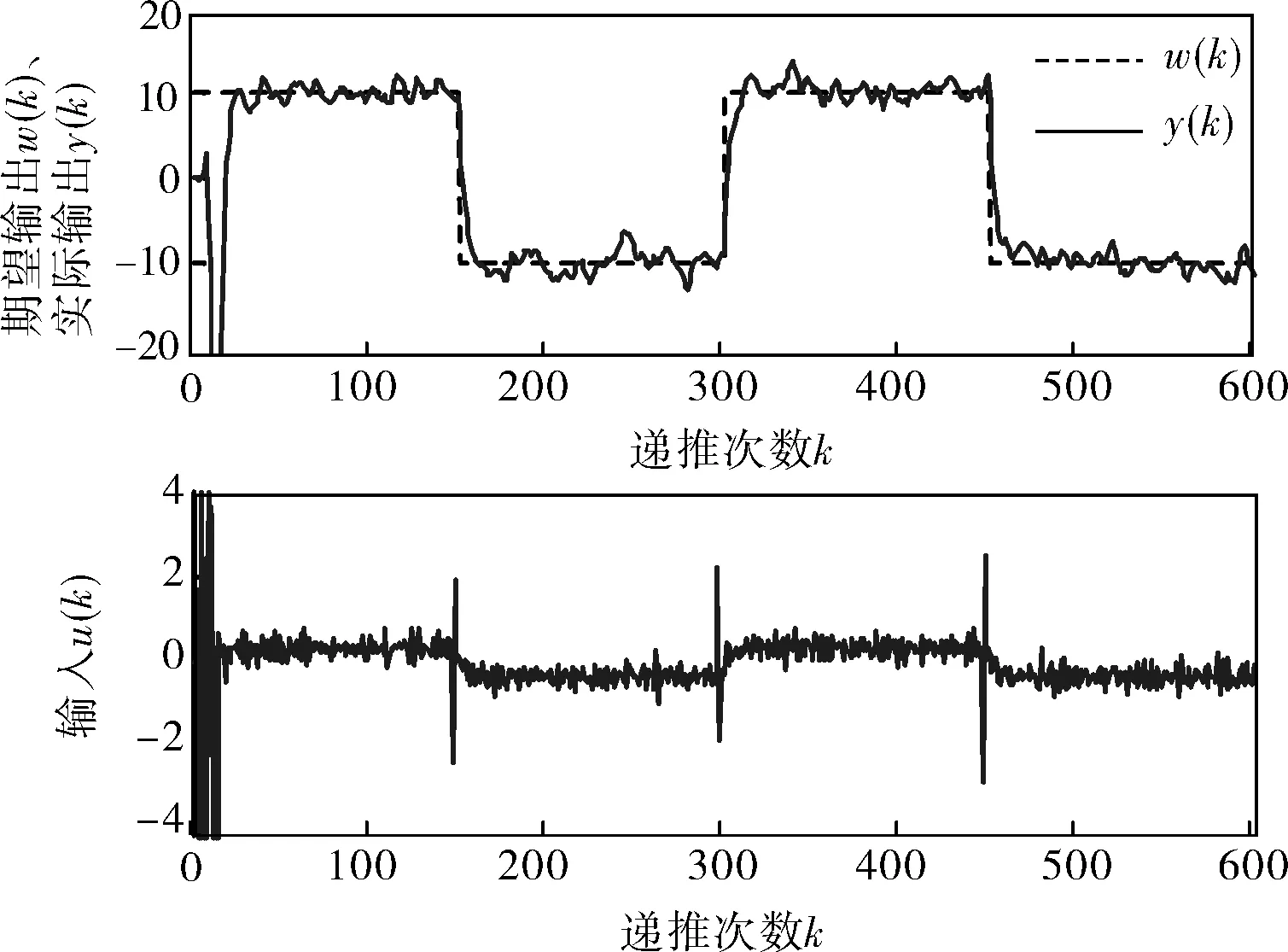
图4 JGPC算法仿真

通过对图2～4的比较发现，GPC自适应算法可以对未知的模型参数进行辨识，对环境具有很好的自适应性，当系统模型参数被辨识出来后，控制信号u的变化不会那么剧烈，但是系统的调节时间可能会有所增加。该算法也有其固有的缺陷，如计算量较大及算法过于复杂等，且在实际应用中还受到C(z-1)稳定的限制。JGPC算法中，实际输出值y(k)与期望输出值w(k)更为接近，该算法适用于C(z-1)不稳定的开环不稳定非最小相位系统，所以在液位控制系统的实验中使用JGPC算法。

2.2 基于CARMA模型的JGPC算法

被控对象的CARMA模型可表示为：

A(z-1)y(k)=z-dB(z-1)u(k)+C(z-1)ε(k)

(1)

其中，y(k)、u(k)、ε(k)是系统的输出、控制量和白噪声；d为纯延时。

由式(1)递推，系统将来时刻的最小方差输出预测模型为：

Y*=Ym+GΔU

(2)

Y*=[y*(k+d+1|k),…,y*(k+N|k)]T

(3)

Ym=[ym(k+d),ym(k+d+1),…,ym(k+N)]T

(4)

ΔU=[Δu(k),Δu(k+1),…,Δu(k+N-d)]T

(5)

(6)

式(4)中的ym(t+k)完全由过去的控制输入和输出确定。

极小化目标函数：

J=E{(Y-Yr)T(Y-Yr)+ΔUTΓΔU}

(7)

得到相应JGPC控制增量为：

ΔU=(GTG+Γ)-1GT(Yr-Ym)

(8)

则当前时刻的控制量为：

u(k)=u(k-1)+Δu(k)

=u(k-1)+[1,0,…,0](GTG+Γ)-1GT(Yr-Ym)

(9)

3 液位控制系统的实验

3.1 参数整定

为知道各参数对液位系统模型的影响，不先对液位模型进行系统辨识。利用MATLAB/Simulink程序开发工具对被控对象进行仿真研究。预测长度N为15时y(k)的振荡非常明显，当N逐渐增大时，振荡减弱，仿真效果改善。当预测长度取20时y(k)达到稳定，仿真效果为最佳，故取N=20。对于遗忘因子λ，在仿真曲线中λ增大到2以后，振荡变大，可得λ最优取值为1。若取输出柔化因子α=0.2，实际输出曲线振荡比较剧烈，随着α的逐渐增加，实际输出w(k)逐渐稳定，但是当α大于0.7时，实际输出曲线与理想输出曲线的契合度变差。所以，α=0.7为最佳。

综上所述，JGPC算法的参数设定为预测长度N=20，遗忘因子λ=1，输出柔化因子α=0.7。

3.2 液位系统的仿真实现

图5 控制效果

图6 对象参数估计结果

通过对参数的整定，得到了较好的仿真结果，有效地控制了液位的稳定。JGPC算法对液位的控制十分有效。

4 结束语

利用MATLAB/Simulink程序开发工具，对广义预测控制进行仿真和实验研究。引入广义预测控制算法，通过分析比较选择改进后的JGPC算法。最后通过双容水箱实际系统应用，验证了这种算法在控制性能上的快速性和稳定性，对将其运用于化工生产液位控制系统具有借鉴意义。