基于生物地理优化算法的神经网络故障诊断方法研究
任伟建 赵月娇 王天任 刘爱君
(1.东北石油大学电气信息工程学院,黑龙江 大庆 163318;2.上海理工大学能源与动力工程学院,上海 200093;3.胜利油田井下作业公司,山东 东营 257077)
自然界中的生物均具有群体行为,种群中的简单个体通过团体协作来实现复杂的工作,这种群智能现象吸引着越来越多的学者。他们模拟借鉴生物群体智能机制,研究相应的群智能优化算法理论并开发高智能的信息处理系统,以解决人类运用传统方法难以解决的问题。遗传算法、粒子群优化算法、蚁群算法及免疫算法等均为群智能优化算法。神经网络是从生理角度模拟人类行为的一种智能技术。该技术已在各行业得到广泛应用[1,2]。可将传统的工程系统和人工智能处理技术混合起来,通过学习、训练和记忆,拟合输入变量与输出变量间的非线性映射。由于神经网络训练常用的学习算法——传统BP算法具有固有的缺陷而影响着应用效果[3],造成神经网络收敛速度慢且易陷入局部极小值。目前BP网络的改进方法有在梯度法基础上改进学习算法、网络拓扑结构优化以及融入其他优化算法等。
鉴于群智能优化算法的优良特性,很多学者应用群智能优化算法代替BP算法进行神经网络的训练。周颖等提出了一种人工免疫学习算法,将其用于RBF神经网络隐层中心点数和位置的调整[4];田文杰等将蚁群算法和神经网络结合起来,应用于设备故障专家系统的知识获取并进行诊断推理[5];文献[6]将粒子群优化算法用于优化神经网络的连接权值和阈值,并将优化好的神经网络应用于故障诊断中。
基于对生物物种迁移、变异行为的研究,以生物地理学归纳计算为理论的生物地理优化算法(Biogeography-based Optimization,BBO)是一种新型的群智能优化算法。鉴于其他群智能优化算法在神经网络训练中的应用,笔者将生物地理优化算法与BP神经网络相结合,建立BBO-BP组合神经网络模型,充分发挥BBO解决优化问题的优势,克服连接权值随机导致神经网络易陷入局部极小值的缺点,缩短训练时间。
1 生物地理优化算法①
生物地理优化算法就是根据生物地理学阐述的生物物种在地理上分布的特点,使用生物地理学的分配机制(即迁移模型、变异生新),以适宜度最优为求解目的,来解决工程问题[7]。具体说就是,待优化问题的解对应着生物地理学中栖息地的特征向量SIV,其中的各种自然因素相当于优化问题解向量的分量;待优化问题的度量函数值f(xi)(i=1,2,…,n)对应着生物地理学中的栖息地适宜度指数HIS,好解类似于高HIS的栖息地,差解类似于低HIS的栖息地;优化算法中的信息交互机制对应着栖息地的移近移出机制,设计了基于概率的个体迁移算子实现信息共享,每个个体通过计算得到各自的移进概率λi和移出概率μi,通过该数值来控制个体信息的移动概率。同时,为增加群体多样性,设计变异算子,根据栖息地容纳种群数量的不同,计算相应的变异率,对栖息地进行变异操作,从而扩大解集。
生物地理优化算法的精髓即迁移操作和变异操作,利用迁移操作与其他栖息地进行信息交换,进而对解空间进行广域搜索;利用变异操作来模拟自然突变,根据栖息地i的种群迁移率对栖息地的特征向量进行突变进而更新解集。
迁移操作。迁移模型采用的是简化线性模型,设栖息地的数量为n,群体大小为NP,优化问题的维度为D,最大物种数为Smax、最大迁出率为Emax、最大迁入率为Imax,具体的流程为:
fori=1 toNPdo
用概率λi选取xi
if(0,1)之间的均匀随机数小于λithen
forj=1 toNPdo
用概率μi选取xj
if(0,1)之间的均匀随机数小于μithen
从xj中随机选取一个SIVσ
用σ替换xj中的一个随机SIV
end if
end for
end if
end for
变异操作。最大变异率为mmax,迁移率为Ps,精英个体保存数量为k,BBO变异操作的核心问题就是如何根据栖息地拥有种群数量的概率给出相应的突变率,具体的流程为:
fori=1 toNPdo
计算概率pi
用概率pi选取SIVxi(j)
if(0,1)之前的均匀随机数小于mithen
用一个随机产生的SIV替换xi(j)
end if
end for
2 生物地理优化算法与其他群智能算法的比较
虽然BBO算法和其他智能算法一样,都属于模拟自然选择和生物进化机制的智能优化算法,但是该算法和其他算法有本质区别,以下为与其他算法的比较。
2.1 与遗传算法的比较
BBO也会在解之间实现信息的共享,但在进化过程中并不产生新的子代,算法利用移进概率来决定栖息地是否需要引入特征变量以及进入的比例,并且移进的特征变量来自其他不同的个体;而遗传算法通过染色体来共享信息,通过交叉变异重组基因单元来产生新的子代,它不能根据适应值来控制交叉基因,并且交叉的基因片段来自于同一个体。
2.2 与蚁群算法(ACO)的比较
BBO是通过迁移机制来改进解的适应度,它并不直接产生新的解集,只是依赖迁移机制来修改这些解;而ACO是通过蚂蚁之间信息素的交换和相互协作来实现优化,在每次迭代过程中要产生新的解集,每一代都会产生一系列方法,而BBO则会保持方法不变。
2.3 与粒子群优化算法(PSO)的比较
BBO同粒子群优化算法最为相似,都是通过个体间的知识分享来达到优化的目的,都将产生的优质方案保存到下一代,每一个方案都和邻近个体进行信息交互,进而进行调整。但BBO采用了根据不同栖息地种群数量来选择不同操作强度的物种激励机制,从而通过迁移机制调整解集来改进解的适应度,而PSO是通过调整粒子的速度和位置来改进粒子的适应度。另一方面粒子群的解更可能聚在一起,而BBO的解没有任何内在聚类的趋势。
从这些不同之处可以看出BBO算法是一种独特的群智能优化算法。
笔者采用典型的Sphere单峰函数和Rastrigin多峰函数进行测试,并与典型的群智能算法——蚁群优化算法、遗传算法和粒子群优化算法进行仿真性能比较。算法对于各个测试函数优化的平均运行结果如图1、2所示。
表1列出了测试函数过程中每一个算法的平均极小值(表示算法的平均性能)和最好极小值(表示算法的最好性能)。
从测试结果可以看出,对于Sphere单峰函数BBO前期收敛速度快,找到最优解的精度没有PSO好;但在处理Rastrigin多峰函数时,BBO的收敛速度快,并且较其他算法最接近优化值。综上所述,BBO处理优化问题还是具有优势的,求解过程中不存在波动,稳定性较好。
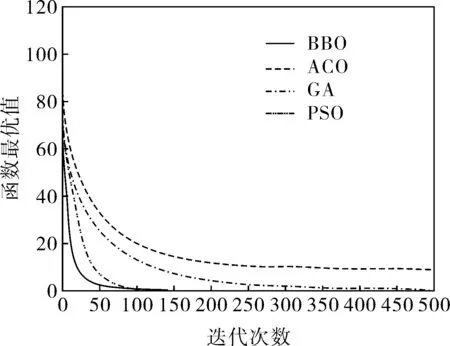
图1 Sphere单峰函数测试结果比较

图2 Rastrigin多峰函数测试结果比较
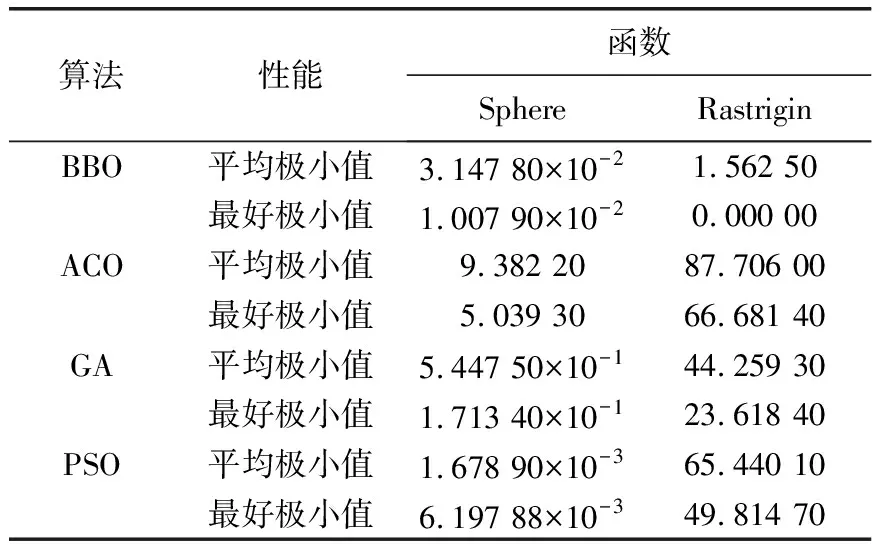
表1 各个算法运行的平均值和最优值
3 基于生物地理优化算法的神经网络故障诊断
基于神经网络的故障诊断中,神经网络的输入是被诊断对象的征兆即特征值,输出则表示发生故障的可能性。在整个诊断过程中,先利用一组故障样本对网络进行训练,确定网络结构和参数,进而实现征兆集与故障集之间的非线性映射。借鉴其他智能算法在神经网络故障诊断中的应用,笔者将BBO算法与基于BP神经网络的故障诊断相结合,把BP神经网络结构中有待训练的权值和阈值看作是BBO算法的寻优目标参数,用BBO算法作为学习算法对BP神经网络的权值和阈值进行训练。
3.1 建立神经网络
笔者选取应用最广泛的三层神经网络,以文献[8]中的抽油机数据(表2、3)为例,输入节点对应电流特征向量的6个分量,输出节点数为3,对应抽油机的3种工作状态。
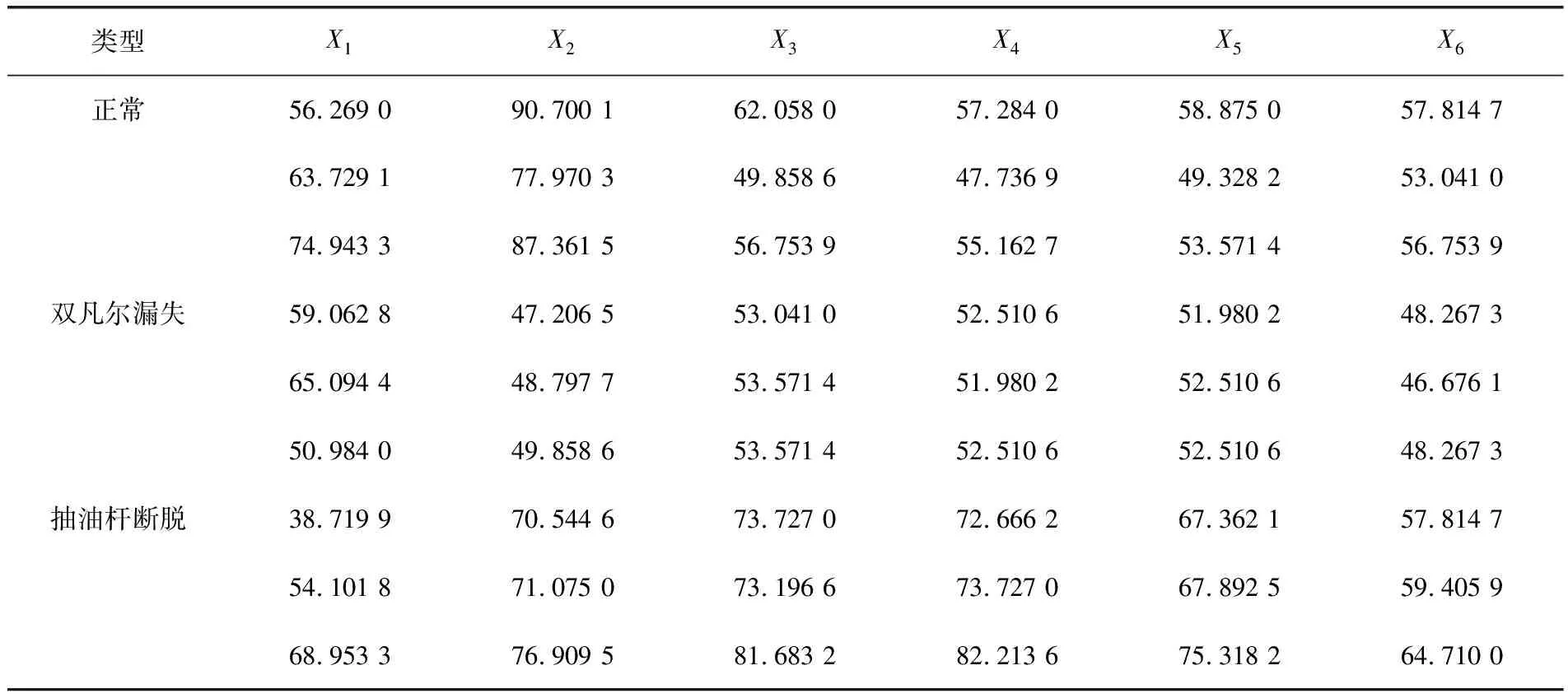
表2 训练样本数据
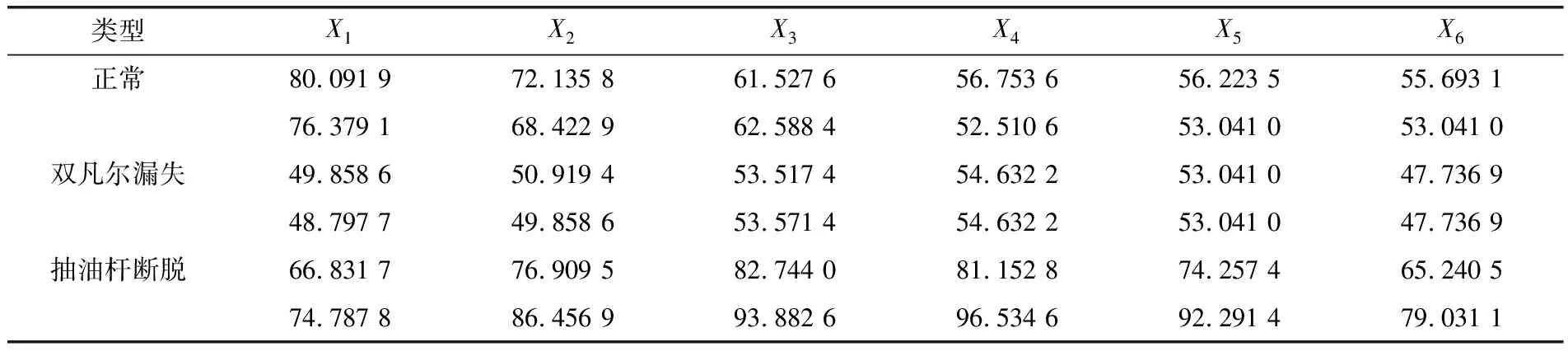
表3 测试样本数据
3.2 确定参数
利用BBO算法训练BP神经网络时,定义生物栖息地适宜度分量为网络中的连接权值。笔者采用6-6-3结构的三层神经网络,权值为6×6+6×3=54,阈值为6+3=9,故栖息地适宜度模型维数为54+9=63。设置群体大小NP=100,Imax=Emax=1.0,最大变异率mmax=0.005,迭代次数为1 000。
3.3 基于BBO算法的神经网络训练
将BBO作为学习算法来优化神经网络权值的关键在于以下两点:
a. 建立BBO的物种维度空间与神经网络连接权值之间的映射。生物地理优化算法中,每个生物栖息地的维度分量都对应为神经网络中的一个连接权值,也就是说神经网络中有多少个连接权值,作为学习算法的BBO中的每个栖息地就应该有多少维。
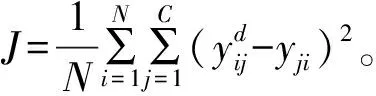
BBO算法训练BP神经网络的流程如图3所示。
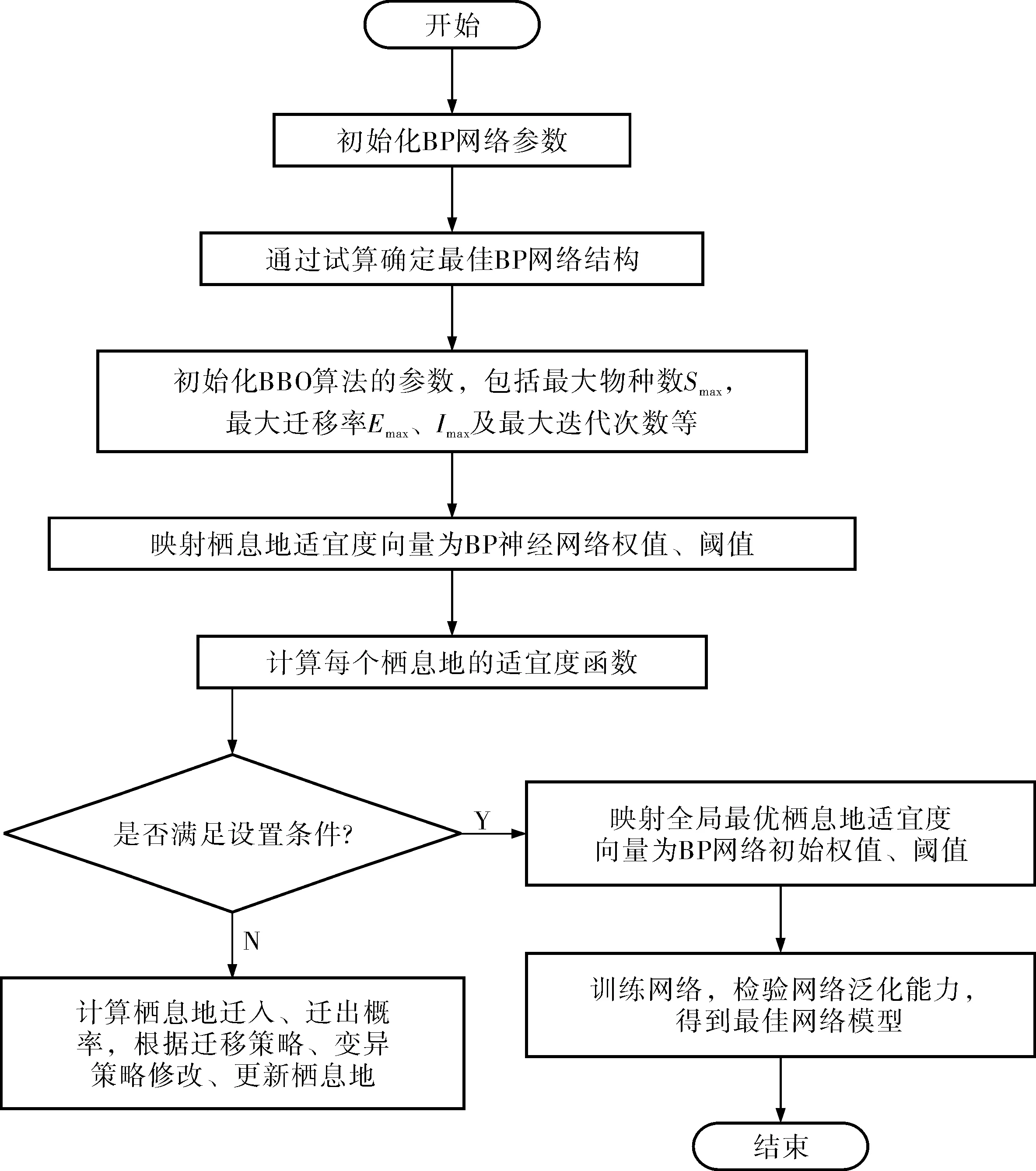
图3 BBO算法训练BP神经网络流程
图4、5为传统BP算法和BBO算法对神经网络的训练曲线。从图中可以看出:在达到目标系统误差10-2时BBO算法迭代次数为653次,要达到相同的误差时,BP算法需要1 194次。在满足相同系统误差的条件下,BBO算法所需训练时间为10.14s,而BP算法所需训练时间为36.18s。经计算,利用BBO算法训练神经网络的均方差为0.301 3,小于利用BP算法训练网络的均方差0.765 8,可见BBO算法不仅提高了神经网络的信息处理速度,并且提高了网络的训练精度。
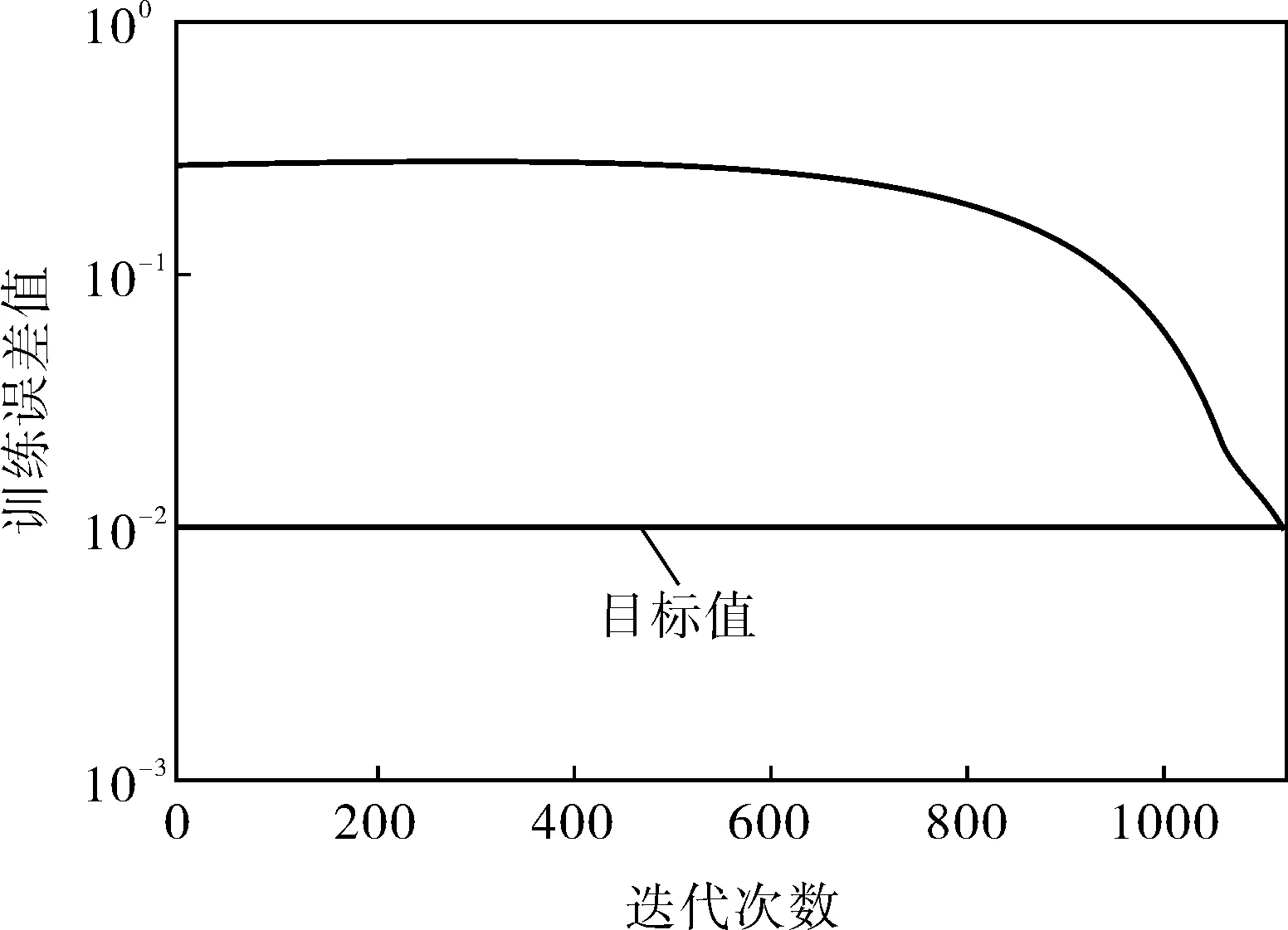
图4 传统BP算法对神经网络的训练曲线
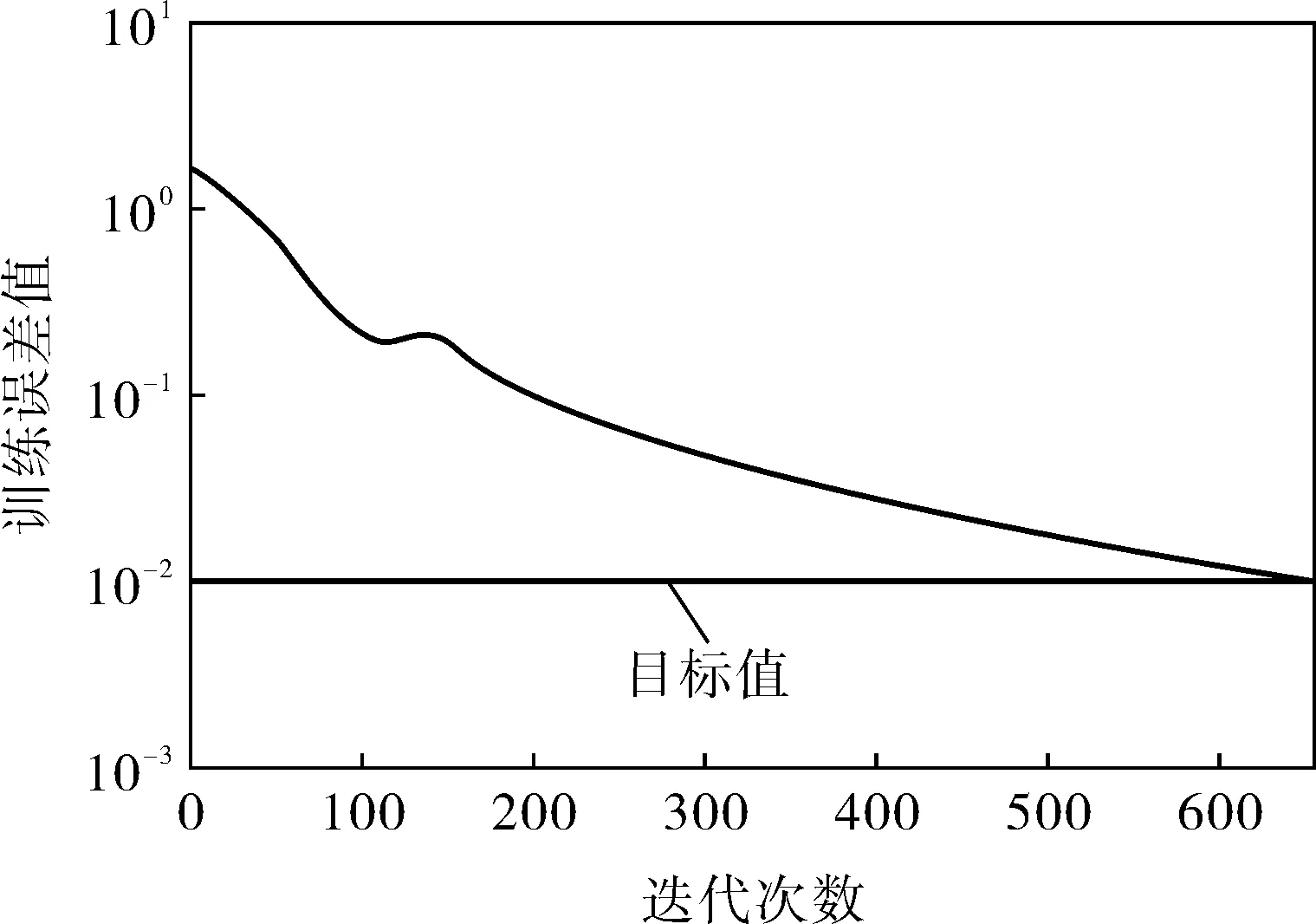
图5 BBO算法对神经网络的训练曲线
3.4 故障诊断结果分析
利用训练好的神经网络对抽油机进行故障诊断,对测试样本数据(表3)进行诊断仿真实验。假定将大于0.5的输出节点值近似看作1,将小于0.5的输出节点值近似看作为0,(1 0 0)、(0 1 0)、(0 0 1)分别对应着正常、双凡尔漏失和抽油杆脱落,诊断结果见表4。
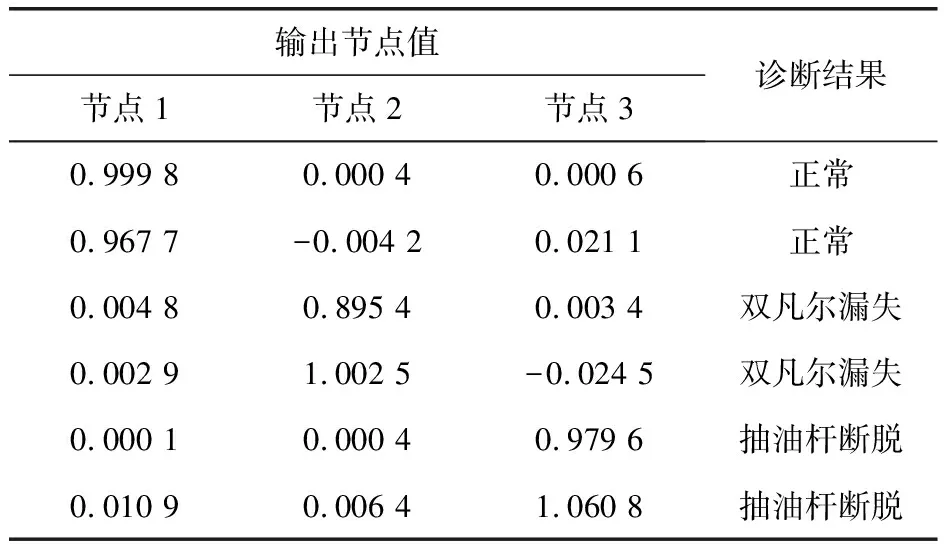
表4 BBO算法诊断结果
从表4可以看出,基于BBO的神经网络的诊断数据接近于理想值,故障区分度较高,因此可以得出结论:利用BBO算法优化神经网络应用于抽油机故障诊断中是可行的,并具有很强的准确性。
4 结束语
阐述了生物地理优化算法的优化原理和算法流程,并将其与其他群智能算法进行比较,通过仿真实验得出,BBO算法具有很强的优势性与良好的发展空间。将生物地理优化算法应用于神经网络的学习训练中,克服了BP算法训练时间较长并容易陷入局部收敛的缺点,而且能更快速地收敛于目标最优解。将训练好的神经网络对抽油机常见故障进行诊断,诊断结果表明:该方法是可行的,并且具有良好的准确性和有效性,具有广泛的应用前景。

