EDA介质中地震波的传播特征*
何现启 朱自强 鲁光银
1) 中国长沙410008湖南省交通规划勘察设计院 2) 中国长沙410083中南大学地球科学与信息物理工程学院
EDA介质中地震波的传播特征*

1) 中国长沙410008湖南省交通规划勘察设计院 2) 中国长沙410083中南大学地球科学与信息物理工程学院
对Christoffel公式进行Bond变换得到EDA介质的Christoffel方程,并由其非零解推导出EDA介质中视横波(qSV)、 横波(SH)、 视纵波(qP)的相速度、 群速度、 偏振向量(质点的振动方向)的三维计算公式. 通过模型计算分析了具有水平对称轴的各向异性(HTI)介质和EDA介质中介质对称轴的极角和方位角对相速度、 群速度及偏振向量的影响, 对其随极角、 方位角的变化特征进行了分析,并采用Matlab进行了数值计算,对其特征采用三维显示. 通过取极角或方位角为零简化得到HTI介质和具有垂直对称轴的各向异性(VTI)介质中地震波的相速度、 群速度, 对EDA介质中的三维计算结果进行退化验证. 通过数值计算进一步验证了地震波相速度与EDA介质对称轴的相互关系. 结果表明,通过广角地震勘探可探明地下介质的裂隙走向及密度, 从而确定灾害体产状.
EDA介质 地震波 相速度 群速度
引言
各向异性的基本模式有两种. 一种是裂隙诱导各向异性EDA (extensive dilatancy anisotropy)模式, 用于描述由彼此平行的垂直裂隙、 微裂隙和定向排列的微细孔洞引起的各向异性. EDA介质广泛存在于地壳中,属于六方晶系,有水平对称轴,对称轴在最小水平应力方向. 另一种是PTL (periodic thin-layery)模式, 用于描述沉积盆地地层的微细层理和旋回性薄层引起的各向异性,也属于六方晶系,但其对称轴是垂直的. 上述两种模式都属于六方各向异性,又称横向各向同性(vertical transverse isotropy, 简称VTI)介质,具有水平对称轴的横向各向同性(horizontal transverse isotropy, 简称HTI)介质可以看成是VTI介质旋转90°得到的.
上述两种基本模式还可以组合,生成具有任意方位的正交晶系的各向异性介质(Crampin,1989; Michael,1994),这种岩层属正交各向异性(orthorhombic anisotropy,简称OA)介质,被称为PTL+EDA介质.
理论和实践均已证明, 地层各向异性普遍存在(梁锴,2009). 其弹性特征随方向变化,致使地震波在地层中传播时,其相速度、 群速度、 偏振方向及衰减也都随方向变化. 目前勘探领域的地震资料处理与解释技术都是基于各向同性理论,处理结果往往存在不同程度的畸变,有时甚至会导致错误的结论,因此各向异性研究也变得越来越重要. 地震各向异性研究也成为地震学研究的热点和难点之一. 开展地震各向异性研究对地质灾害预报、 隧道安全监测、 工程检测、 地下水勘探、 复杂油气藏勘探开发等方面具有重要的理论和实用价值.
相速度与群速度是认识各向异性地震波传播规律的主要参数. 本文在研究弹性HTI介质地震波传播特征的基础上,推导出EDA介质中地震波的相速度、 群速度及偏振方向的计算公式,研究其随裂隙方位的变化规律,以进行工程地质灾害预报和安全监测等.
1 EDA介质中地震波的相速度
地震波在各向异性介质与各向同性介质中的传播特征有诸多不同之处, 其一便是在各向同性介质中相速度与群速度始终都是等价的, 而在各向异性介质中, 平面波的相速度与群速度通常在大小和方向上都不一致, 且其在方向上的差别即使在弱各向异性条件下也不能忽略, 只有在极少数特殊方向上相速度与群速度才完全相等. 相速度是最基本、 最重要的物理量之一, 许多其它物理量都需要基于它来导出; 此外, 许多物理定律(例如 Snell定律)的数学形式也需要用相速度或相慢度来表示.
各向异性介质中平面波的相速度平方是Christoffel矩阵的特征值, 可由Christoffel特征方程求解. 下面主要通过HTI介质中地震波的Christoffel方程求解EDA介质的地震波相速度.
各向异性介质均可采用6×6的弹性刚度矩阵表示. 一般情况下,弹性参数都是在本构坐标系(以对称轴为坐标轴)中给出的. 实际上在正演和反演问题中,为了简化运算,本构坐标系与观测坐标系之间的转换是必不可少的. 根据欧拉旋转理论,三维空间内的任意旋转均可用3个欧拉角描述. 对于6×6的弹性刚度矩阵C,Bond(1943)给出了如下变换矩阵(Bond矩阵):
(1)
式中,aij为新旧坐标轴[(a,b,c), (x,y,z)]间的余弦. 这样,新坐标系下的弹性系数矩阵可以进一步表示为

图1 EDA介质中地震波的传播参数示意图Fig.1 The schematic diagram of propagation parameters of seismic wave in EDA media
(2)
根据各向异性理论,EDA介质的弹性刚度矩阵可由HTI介质的弹性刚度矩阵旋转得到. 从Christoffel方程可以看出,相速度V2和偏振向量分别是Christoffel方程的特征值和特征向量. 相速度可由Christoffel 特征方程求出.
令P=(px,py,pz)T为偏振方向,n=(nx,ny,nz)T=(sinθcosφ, sinθsinφ, cosθ) 为传播方向, 其中θ和φ分别为传播方向的极化角和方位角,如图1所示.
由HTI介质的弹性矩阵,经Bond变换(刚度矩阵的坐标旋转变换)(Winterstein,1990),可得到EDA介质的Christoffel方程如下:
(3)
式中
(4)
若使式(3)有非零解, 须有detΓ=0. 式(4)中的cij是由HTI弹性矩阵经Bond变换后得到的EDA弹性矩阵中的元素,而不是HTI介质弹性矩阵中的元素,具体表达如下:
(5)

(6)
求解方程(6)可得EDA介质中的qP波、 qSV波和SH波的相速度(张百红等, 2010; 王观石等, 2010)为
(7)
其中
(8)
当θ=π/2时,即xoy平面内二维相速度为
(9)
其中
D=[(c11-c55)cos2(φ-φ0)-(c22-c55)sin2(φ-φ0)]2+
4(c13+c55)2sin2(φ-φ0)cos2(φ-φ0).
当EDA介质对称轴倾角φ0=0时,EDA介质就退化为HTI介质,其地震波相速度为
(10)
其中D=[(c11-c55)cos2φ-(c33-c55)sin2φ]2+4(c13+c55)2sin2φcos2φ.
2 EDA介质中弹性波的群速度
在均匀各向同性介质中,相速度不随传播方向变化,相速度面与群速度面重合; 在各向异性介质中,相速度不再保持恒定,而是随传播方向而变化,这时群速度面不再与相速度面重合. 在完全弹性各向异性介质中,群速度等价于能量的传播速度,因此实际观测到的一般是群速度和群角,而相速度和相角只有在某些特殊角度或采用特殊手段才能观测到. 根据推导各向异性介质中群速度的思路(Crampin,1981),将式(7)代入极端各向异性介质中地震波群速度方程(Crampin, 1981; 郝重涛,姚陈,2007; 何现启, 2010)可得:
1) qP波的群速度
(11)
式中,D,E和F的计算公式同式(8),G=(cosφsinθcosφ0+sinφsinφ0).
2) qSV波群速度
(12)
式中D,E,F和G的计算公式同式(8).
3) SH波群速度
(13)
式中G和E的计算公式同式(11).
3 EDA介质中弹性波的偏振方向
偏振向量是一个表示质点位移方向的单位矢量. 由Christoffel方程可以看出,偏振向量是Christoffel的特征向量,可由Christoffel 特征方程求出. 将qP波、 qSV波和SH波的相速度分别代入介质Christoffel方程并求解方程,其通解为该种波型的偏振向量(表示质点位移方向的矢量). 求解各种波型的偏振向量如下:
1) SH波偏振矢量
(14)
式中c为任意常数(下同). 由上式可知PSH×n=0,说明EDA介质中SH波的偏振方向PSH与传播方向n[=(nx,ny,nz)T=(sinθcosφ, sinθsinφ, cosθ)]垂直,为纯SH波.
2) qP波偏振矢量
(15)
由上式可知gP×n≠0,说明EDA介质中P波的偏振方向与其传播方向不平行(在各向同性介质中P波的偏振方向与传播方向平行),有一定夹角,因此称EDA介质中的P波为视P波或qP波.
3) qSV波偏振矢量
(16)
由上式可知gSV×n≠0,说明EDA介质中SV波的偏振方向与其传播方向不垂直(在各向同性介质中SV波的偏振方向与传播方向垂直),呈一定夹角,因此称EDA介质中SV波为准SV波或qSV波.
4 模型计算
为了检验HTI与EDA介质中地震波相速度、 群速度及偏振向量公式的正确性与实用性,需对其进行数值计算. 下面给出两个模型,分别对 HTI 介质与 EDA介质中的相速度、 群速度和偏振向量进行计算.
4.1 HTI介质的模型计算
弹性介质模型的性质是由刚度矩阵C确定的,刚度矩阵C确定了应力与应变之间的关系,但由其确定的弹性波动方程系数的物理意义很不直观,由此导致波传播的相速度隐含在波动方程的系数中,其物理意义既不明确,也很复杂. 为方便理论研究和实际应用,围绕波传播的相速度公式,Thomsen(1986)提出了一套表征横向各向同性介质弹性性质的参数,定义如下:
(17)
式中,ε,γ,δ为无纲量. 参数γ表示qSH波的严格速度解,ε和δ表示qP波和qSV波的近似速度解. 这3个参数的取值大小反映了介质的各向异性程度,值越大各向异性越强.
由Thomsen(1985, 1986)参数建立HTI模型(模型1)和EDA模型(模型2),所描述的HTI介质各向异性模型及其参数如图2和表1所示.
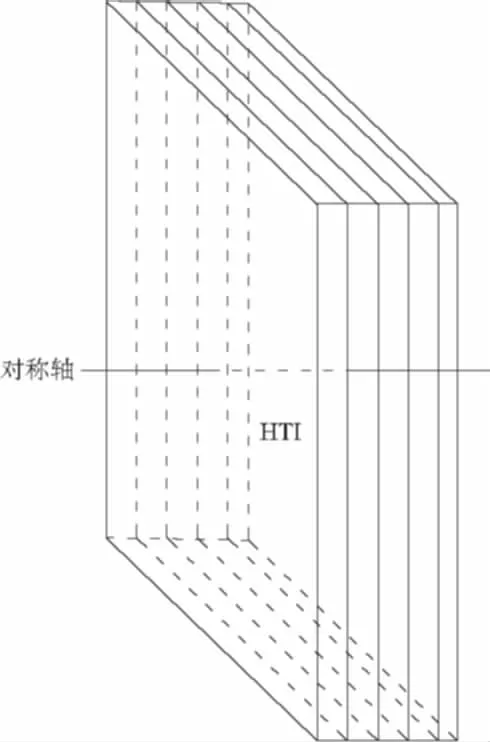
图2 HTI模型Fig.2 HTI model 表1 HTI模型参数 Table 1 Parameters of HTI model

VP0/(km·s-1)VS0/(km·s-1)εδγρ/(g·cm-3)2.891.7680.2-0.20.22.42
由垂直速度和各向异性系数直接计算HTI介质的弹性矩阵如下:

(18)
将HTI介质的弹性系数矩阵代入相速度公式(何现启,2010), 计算得到HTI介质中地震波的相速度,并用Matlab对结果进行三维显示,结果如图3所示. 图3给出了依据模型1计算的P波、 SH波和SV波的三维相速度. 从图3可看出,P波的相速度为一具有水平对称轴的不规则椭圆,SH波相速度为一具有水平对称轴的规则椭圆,SV波相速度为具有水平对称轴的不规则圆柱体. 图4为图3的切片图,通过不同切片研究相速度随极角、 方位角的变化特征. 图4a显示方位角为0°时,P波相速度随极角的变化为一不规则椭圆,椭圆的长轴指向极角为零的方向(水平方向); 图4b显示极角为90°时,P波相速度随方位角的变化为一不规则椭圆,椭圆的长轴指向极角为零的方向(方位角为90°的方向); 图4c显示方位角为90°时,P波相速度不随极角变化,即方位角为90°时,各方向上的P波相速度大小相等.

图3 模型1: HTI介质中P波(a)、 SH波(b)和SV波(c)的相速度 图中球面表示各方向上相速度的大小

图4 模型1: HTI介质中地震波的相速度(VP)与极角(θ)和方位角(φ)的关系 (a) φ=0°; (b) θ=90°; (c) φ=90°. 图中蓝色线表示各方向相速度的大小,单位为km/s
以上结果显示,HTI介质中各方向上的地震波相速度不同,呈现方向各向异性,但相速度具有一水平对称轴,且与介质的对称轴一致.
将HTI介质的弹性系数矩阵式(18)代入群速度公式(何现启,2010),计算得到HTI介质中地震波的群速度,并用Matlab进行三维显示(图5). 由图5可看出,HTI介质中群速度与相速度具有类似特征,但其各向异性特征更为显著.
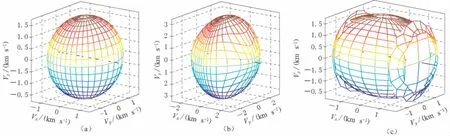
图5 模型1: HTI介质中SH波(a)、 P波(b)和SV波(c)的群速度
将HTI介质的弹性系数矩阵式(18)代入偏振向量计算公式(何现启,2010),计算得到HTI介质中地震波的偏振向量,并用Matlab进行三维显示,如图6所示.
由图6可知,在HTI介质中纵波的偏振方向不再与波的传播方向平行而是呈一定夹角,因此被称为视纵波(qP波); 横波SV波的偏振方向不再与波的传播方向垂直而是呈一定夹角,因此称为视横波(qSV波); SH波的偏振方向仍然与传播方向垂直.
分析图3—6, 依据相速度和群速度表达式及其随方向的变化特征,可知HTI与VTI介质中地震波的特征很相似,只是其对称轴一个为水平方向另一个为垂直方向. 如果HTI介质弹性系数是由VTI旋转而得到,那么其相速度与群速度的椭圆形状将完全一致. 由图4可看出,在HTI介质中xoz和xoy为各向异性面,即相速度和群速度是随角度变化的,也就是所说的角散现象. 在yoz平面内,相速度与极角无关,即yoz为各向同性面. 而在VTI介质中xoy平面为各向同性面. 在HTI介质中SH波的偏振方向仍与波的传播方向垂直,而P波的传播方向则与偏振方向呈一夹角,尤其是SV波的偏振方向与其在各向同性介质中的偏差最为明显.
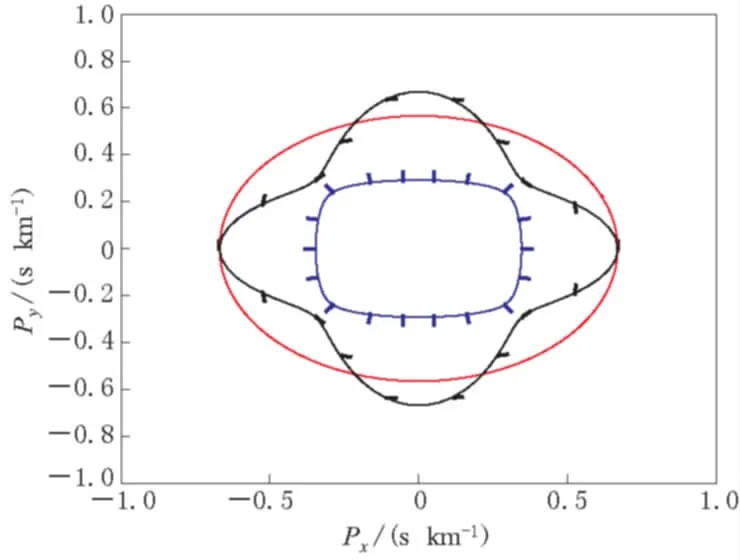
图6 模型1: HTI介质中qP波、 qSV波和SH波慢度面与偏振方向的关系 图中红色、 黑色、 蓝色分别表示qP波、 qSV波和SH波,短划线表示 其偏振方向,连线表示其慢度面
4.2 EDA介质的模型计算
首先采用Thmosen (1986, 1995)参数建立一个HTI模型(模型1),再通过Bond变换得到EDA介质模型,即模型2,其参数见表2.

表2 EDA模型的参数
将HTI介质的弹性系数矩阵式(18)进行Bond变换(将对称轴绕z轴逆时针旋转60°), 得到EDA介质的弹性系数矩阵如下:
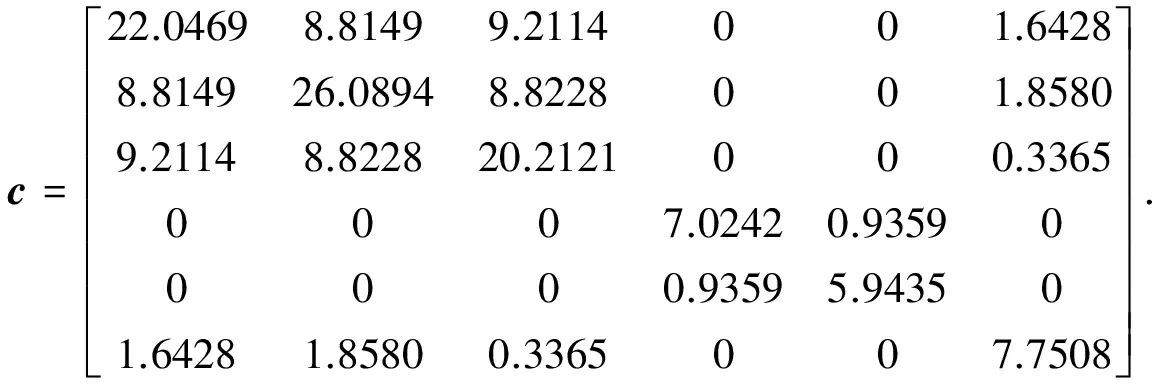
(19)
将EDA弹性系数矩阵式(19)代入式(7), 计算得到EDA介质中地震波的相速度,并用Matlab进行三维显示,如图7所示.

图7 模型2: EDA介质中P波、 SH波和SV波的相速度 (a) 平视图; (b) 俯视图
图7a为依据模型2,即EDA模型,计算的P波、 SH波和SV波的三维相速度. 由该图可见,P波和SH波的相速度为一具有水平对称轴的不规则椭圆,SV波的相速度为具有水平对称轴的不规则圆柱体. 图7b为图7a的俯视图,由该图可见水平对称轴与介质模型的对称轴一致,相速度的对称轴在水平面内逆时针旋转了60°.
将EDA弹性系数矩阵式(19)分别代入式(11)、 (12)和(13),计算得到EDA介质中地震波的群速度,并用Matlab进行三维显示(图8).
图8显示了EDA介质中地震波群速度和相速度具有相似特征,其随方向的变化均为一近视椭球,椭球的长轴与介质的对称轴方向一致. 图9显示了EDA介质中P波相速度随极角、 方位角的变化特征,两者均为近似椭圆.
在式(7)中,取方位角为60°,即可得到EDA介质中相速度随极角的变化情况(图9a); 取极角为0°即可得到EDA介质中相速度随方位角的变化情况(图9b).
由图7—9可以看出,相速度和群速度既随着对称轴旋转也绕z轴旋转,其短轴方向指向介质的对称轴方向, 长轴方向指向介质的裂隙走向方向,由此在实际勘探中可由速度分析确定地下介质主要裂隙的走向.
将EDA弹性系数矩阵式(19)分别代入式(14)、 (15)、 (16),计算得到EDA介质中地震波的偏振向量,并用Matlab进行三维显示,如图10所示.
图10显示了EDA介质中SH波的偏振方向与波的传播方向垂直; qP波的偏振方向与传播方向不再平行,而是呈一定夹角; qSV波的偏振方向与传播方向不再垂直,而是有一夹角.
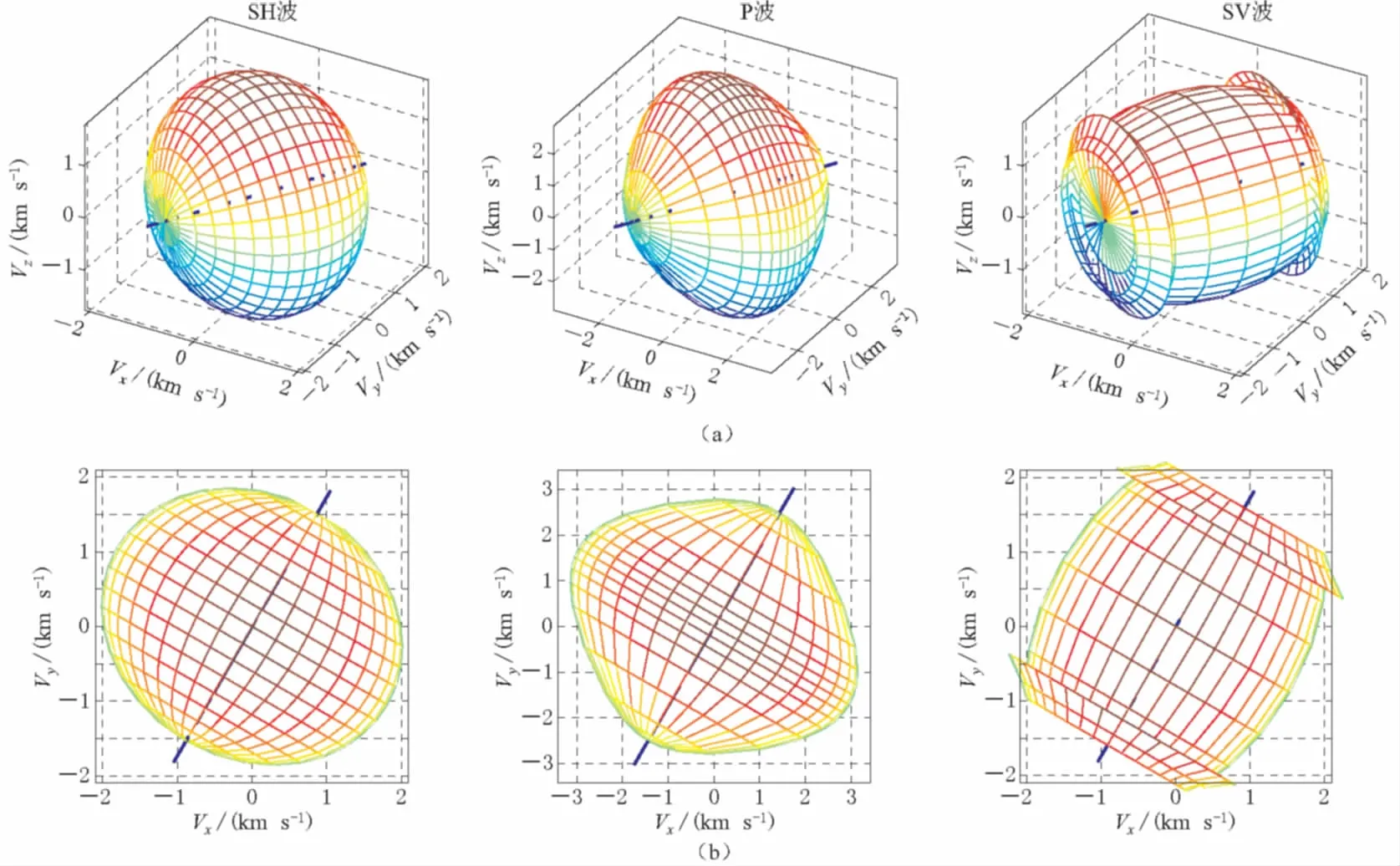
图8 模型2: EDA介质中SH波、 P波和SV波的群速度 (a) 平视图; (b) 俯视图
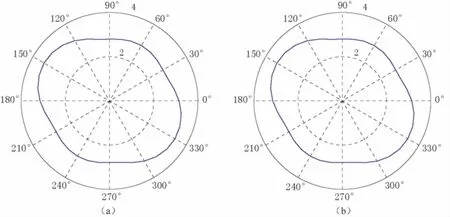
图9 模型2: EDA介质中P波相速度(km/s)与极角(a)和方位角(b)的关系
图10a为EDA介质中地震波的慢度面与偏振方向在xyz坐标系中的计算结果,由于此时介质的对称轴与x轴有一定夹角,因此图10a的计算结果可看作是慢度面在xoy平面内的投影; 图10b为慢度面及介质对称轴旋转后的偏振向量计算结果,此时模型的对称轴与旋转后的x轴重合,计算结果与HTI介质完全一致.

图10 模型2: EDA介质中地震波的慢度面与偏振方向 (a) 在xyz坐标系中的计算结果; (b) 坐标旋转后模型计算结果. 蓝色、 黑色和红色 闭合线分别表示qP波、 qSV波和qSH波的慢度面,短画线表示其相应的偏振方向
5 讨论与结论
基于Bond(1943)的研究成果,由HTI介质的Christoffel方程,通过旋转对称轴得到EDA介质的Christoffel方程,通过求解该方程,得到了EDA介质中三维qP波、 qSV波和SH波的相速度、 群速度及偏振向量的表达式,并通过取极角及方位角为零进行退化验证.
本文在推导公式的基础上,通过模型计算进一步分析了HTI和EDA介质中相速度、 群速度随极角、 方位角的变化情况,分析了EDA介质中地震波的偏振特征,及其与垂直入射的VTI介质、 各向同性介质中地震波的偏振向量区别,验证了EDA介质中相应的计算公式,并利用Matlab进行三维显示,使其传播特征更为形象、 直观. 在HTI介质中xoz和xoy为各向异性面,即相速度和群速度是随角度变化的,也就是所说的角散现象; 在yoz平面内,相速度与速度和极角无关,即yoz为各向同性面. 而在VTI介质中xoy平面为各向同性面. 在HTI介质中,SH波的偏振方向仍与波的传播方向垂直,而P波的传播方向与偏振方向呈一夹角,尤其是SV波偏振方向与各向同性介质的偏差最为明显.
由文中分析可知,EDA介质可以看作是由HTI介质绕z轴旋转一定角度得到的,而HTI介质可以看作是EDA介质的特例. 在实际计算中通过坐标旋转可以使EDA介质中地震波传播特征的计算变得更为简单. 由于地震波的许多传播特征是与EDA介质对称轴与地震测线的夹角有关,并随着夹角的变化而变化,因此我们可利用这一特性对EDA介质进行参数反演. 在实际勘探中,可依据不同方位角的数据得到不同方位的速度,从而确定EDA介质的对称轴方位,进而确定裂隙的走向. 这为实际地震勘探的测线布置及数据解释提供了较好的理论基础.
郝重涛,姚陈. 2007. 任意空间取向TI介质中体波速度特征[J]. 地球物理学报, 50(2): 226--235.
Hao C T, Yao C. 2007. Analysis of body-wave velocity characteristic for TI medium with arbitrary spatial orientation[J].ChineseJournalofGeophysics, 50(2): 226--235 (in Chinese).
何现启. 2010. EDA介质中地震波的传播特征及参数反演研究[D]. 长沙: 中南大学地球科学与信息物理学院: 10--55.
He X Q. 2010.TheStudyofSeismicWavePropagationinEDAMediumandParametersInversiom[D]. Changsha: School of Geosciences and Info-physics, Central South University: 10--55 (in Chinese).
梁锴. 2009. TI介质中地震波的传播特征与正演方法研究[D]. 北京: 中国石油大学地球物理与信息工程学院: 21--58.
Liang K. 2009.TheStudyonPropagationFeatureandForwardModelingofSeismicWaveinTIMedia[D]. Beijing: College of Geophysics and Information Engineering, China University of Petroleum: 21--58 (in Chinese).
王观石, 胡世丽, 李贵荣. 2010. 爆破地震波在结构面的传播特性与结构面倾角判断[J]. 岩石力学与工程学报, 29(9): 1790--1798.
Wang G S, Hu S L, Li G R. 2010. Transmission attributes of blasting seismic wave in interface and judgment of interface obliquity[J].ChineseJournalofRockMechanicsandEngineering, 29(9): 1790--1798 (in Chinese).
张百红, 张秀勇, 钟传利. 2010. 利用纵波探头测定层状岩石的弹性常数[J]. 岩土工程学报, 32(6): 861--866.
Zhang B H, Zhang X Y, Zhong C L. 2010. Elastic constants of foliated rock by use of P-wave probes[J].ChineseJournalofGeotechnicalEngineering, 32(6): 861--866 (in Chinese).Bond W L. 1943. The mathematics of the physical properties of crystals[J].BellSystemTechnicalJournal, 22(1): 1--72.
Crampin S. 1981. A review of wave motion in anisotropic and cracked elastic media[J].WaveMotion, 3(4): 343--391.
Crampin S. 1989. Suggestions for a consistent terminology for seismic anisotropy[J].GeophysicalProspecting, 37(7): 753--770.
Michael S. 1994. Transversely isotropic media equivalent to thin isotropic layers[J].GeophysicalProspecting, 42(89): 885--915.
Thomsen L. 1986. Weak elastic anisotropy[J].Geophysics, 51(10): 1954--1966.
Thomsen L. 1995. Elastic anisotropy due to aligned cracks in porous rock[J].GeophysicalProspecting, 43(6): 805--829.
Winterstein D F. 1990. Velocity anisotropy terminology for geophysicists[J].Geophysics, 55(1): 1070--1088.
The exact propagation characteristics of seismic wave in EDA media

1)HunanProvincialCommunicationsPlanning,Survey&DesignInstitute,Changsha410008,China2)SchoolofGeosciencesandInfo-physics,CentralSouthUniversity,Changsha410083,China
Based on the Christoffel equation,the Christoffel equation of EDA (extensive dilatancy anisotropy) medium is derived by Bond transformation. The exact formulas for 3-D phase velocity, group velocity and polarization vector are derived from the nonzero solutions of the Christoffel equation. The influences of polar and azimuth of symmetry axis of HTI (horizontal transverse isotropy) and EDA media on phase velocity, group velocity and polarization vector are studied through numerical calculation and the results are displayed by 3D graph using Matlab, which makes the results more colorful and intuitive. By setting the polar and azimuth to zero, the phase velocity, group velocity of HTI and VTI (vertical transverse isotropy) media are derived, the 3D phase velocity, group velocity of EDA media are verified by degeneration. The result proves that it is possible to explore the azimuth of cracks, crack density, the occurrence of hazard body by azimuth seismic exploration.
EDA media; seismic wave; phase velocity; group velocity
10.3969/j.issn.0253-3782.2014.03.006.
国家自然科学基金(41174061)资助.
2012-11-26收到初稿,2013-01-20决定采用修改稿.
e-mail: hexqi666@hotmail.com
10.3969/j.issn.0253-3782.2014.03.006
P315.3+1
A
何现启, 朱自强, 鲁光银. 2014. EDA介质中地震波的传播特征. 地震学报, 36(3): 403--416.
He X Q, Zhu Z Q, Lu G Y. 2014. The exact propagation characteristics of seismic wave in EDA media.ActaSeismologicaSinica, 36(3): 403--416. doi:10.3969/j.issn.0253-3782.2014.03.006.

