关于中村(Nakamura)方法分析结构响应有效性的讨论*
罗桂纯 李小军 王玉石 卢 滔
1) 中国北京100081中国地震局地球物理研究所 2) 中国北京100080北京市地震局 3) 中国河北三河065201防灾科技学院防灾工程系
关于中村(Nakamura)方法分析结构响应有效性的讨论*

1) 中国北京100081中国地震局地球物理研究所 2) 中国北京100080北京市地震局 3) 中国河北三河065201防灾科技学院防灾工程系
日本学者中村(Nakamura)1989年提出了一种基于同一地表测点地脉动水平分量与竖向分量傅里叶振幅谱比值来估计场地特征的方法,即所谓的中村方法. 该方法被广泛应用于场地特征的估计,并已取得大量的成果. 目前,这一方法也被国内外的研究人员用来进行结构响应特征的研究. 但中村方法的合理性,国内外尚存在较大争议. 通过对北京城区的一栋钢筋混凝土框架结构建筑的脉动观测,采用中村方法对获取的速度记录进行了计算分析. 结果表明,该方法能有效地得到结构的自振频率,但是不能给出结构对振动的真实放大倍数,因此,在使用此方法分析结构响应方面时应谨慎,建议采用多种方法进行比较分析.
中村(Nakamura)方法 H/V谱比 结构响应 有效性
引言
在Borcherdt(1970)提出参考基岩台计算沉积层场地放大效应的基础上,20世纪80年代末,日本学者中村(Nakamura,1989)提出了一种基于同一地表测点地脉动水平分量与竖向分量傅里叶振幅谱比值(H/V ratio)来估计场地特征的方法,这一方法通常称为中村方法(Nakamura’s technique)或QTS法(Quasi-transfer technique),也简称H/V谱比法.
卢滔等(2006)通过唐山响嘡局部场地影响台阵的记录数据,统计分析了基于该方法估算场地特征成立的前提条件的合理性. 陈棋福等(2008)记录了北京五环路以内600多个点位的脉动背景噪声,并利用H/V谱比法进行计算,得到了北京城区高分辨率的沉积层卓越频率分布. 近年来,很多研究人员将H/V谱比法从场地效应拓展运用到建筑结构对环境噪声的响应研究中. 例如,Gallipoli等(2004)基于地脉动噪声,利用H/V谱比法,研究了地基与结构之间的相互作用和影响; Facke等(2006)利用H/V谱比法对脉动噪声进行计算,估算了德国Cologne教堂的自振频率; 罗桂纯等(2011)基于建筑结构对脉动噪声的响应,利用H/V谱比法估算了钢筋混凝土建筑结构的自振频率.
尽管如此,对于利用中村方法分析结构响应的合理性,国内外仍存在较大的争议. 事实上,将H/V谱比法运用到建筑结构,其原理与在场地土层运用的原理是一样的. 如图1所示,建筑结构相当于场地土层,结构的基底面相当于基岩顶面,不同高度的楼层相当于不同厚度的土层. 结构的基底面与不同楼层上对应水平分量和竖向分量的傅里叶振幅谱分别为SBH,SBV,SSH,SSV.
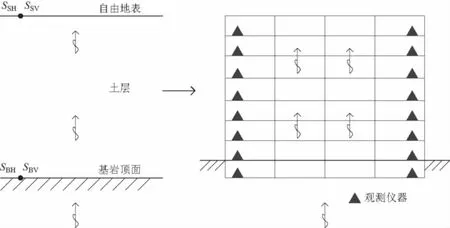
图1 场地土层与建筑结构原理对比示意图
由传递函数法可知,在建筑结构中,从结构基底面到任一楼层的水平分量的传递函数可以表示为
(1)
经变换得
(2)
式中,TF为传递函数; H/V表示水平向与竖向傅里叶振幅谱比值,其中,下标B表示结构基底面,S表示不同楼层; HS/VS代表不同楼层处谱比值,HB/VB代表结构基底面处谱比值. 对应中村方法在建筑结构中的运用,是否满足Nakamura(1989)提出的假定: ① 结构基底面处HB/VB谱比值为1,即SBH/SBV=1? ② 竖向传递函数为1,即SSV/SBV=1?
只有满足条件①和②时,传递函数TFH=HS/VS才成立,才可将不同楼层处的HS/VS作为结构中不同楼层的水平分量传递函数. 同时讨论能否把谱比峰值点对应的频率作为结构的自振频率,谱比值作为结构的放大系数.
本文通过在北京城区的一栋钢筋混凝土框架结构建筑的脉动观测,对每层获取的加速度记录,进行水平向与竖向傅里叶振幅谱比值、 水平向及竖向传递函数、 自振频率和放大系数等的分析. 在此基础上,对H/V谱比法分析结构响应的有效性进行讨论,并给出一些可供参考的建议.
1 观测系统
观测大楼是一栋典型钢筋混凝土结构的建筑,建于20世纪80年代. 该大楼长80 m,宽15 m,高25.3 m,共有8层,包括1层地下室和7层地上楼层,基本结构如图2所示. 大楼位于路北,与楼前的交通主干线和地铁线平行,长轴呈EW方向,短轴呈NS方向,西端是自由端,东端和另一幢大楼相连. 用于记录脉动信号的仪器是REFTEK数据采集系统和Guralp CMG-40T-1短周期地震仪. 该仪器对于30 s—100 Hz的频带有很好的频响,仪器的采样率是200 sps. 从地下室到顶层,每层均在东西两端各布设一台仪器,整个观测系统由16台仪器组成,仪器分布如图2中的三角形所示. 观测从周五晚上开始,一直持续到周一早上,为期60多个小时. 由于观测时间是周末,观测期间人为扰动较少,信号质量较高.

图2 仪器(三角形)布设位置和大楼EW向结构截面图
2 钢筋混凝土建筑结构响应分析
2.1 利用H/V谱比法分析结构的自振频率
建筑结构自振频率(周期)是一个重要的设计参数,是判断建筑结构是否合理的一个重要依据,是衡量建筑结构质量与刚度是否匹配、 刚度是否合理的重要指标(梁远森等,2005). 研究建筑结构的自振频率,能够了解建筑结构自身固有的动力学特征,能够有效地避免建筑结构自振频率与场地卓越频率发生共振而加重结构地震破坏,并针对建筑结构所在场地的特征,提供结构的防震减灾建议,这项工作也能为地震中建筑结构的破坏程度快速鉴定提供依据(罗桂纯等,2011).
为了验证利用H/V谱比法能否快速有效地得到结构的自振频率,首先,利用H/V谱比法对建筑结构中的脉动记录进行计算分析. 为了对比研究,先对建筑物结构中观测到的脉动记录进行快速傅里叶变换(fast Fourier transform, 简写为FFT). 图3给出了五楼西端的仪器记录到的三分量(EW,NS,UD)脉动信号的傅里叶振幅谱. 三分量速度记录的FFT显示,水平分量(EW、 NS分量的合成)的振动频率峰值是在3 Hz和10 Hz左右最明显. 除此之外,EW分量在5 Hz处也有一个小的峰值. 同时,竖向分量在3 Hz处有一个小的峰值,在10 Hz处有一个最为明显的峰值. FFT结果显示,这栋钢筋混凝土大楼的振动频率,在2—20 Hz比较明显,其中最为显著的是3 Hz,5 Hz和10 Hz左右的频率. 这么宽的频率范围,哪个频率才是大楼的自振频率? 根据以往的经验和研究表明,2—3 Hz是大楼的自振频率,5 Hz是大楼的扭转频率,10 Hz是结构对大楼附近交通噪声的响应频率. 傅里叶振幅谱的振动频率太宽,峰值太多,不能分辨出大楼的自振频率. 为了与简单的FFT分析结果进行对比,凸显大楼振动的频率特征,我们计算了大楼第五层西端的SSEW/SSV,SSNS/SSV,SSH/SSV振幅谱比值(为简单起见,这些谱比值分别用EW/V、 NS/V和H/V来代替),如图3b所示. EW/V、 NS/V和H/V的振幅谱比值结果显示,这栋大楼最强的振动发生在2—3 Hz左右,这个特征非常显著; 其次还有两个很小的峰值,分别是5 Hz的扭转频率和10 Hz的交通噪声响应频率,它们几乎可以忽略. 原来FFT中很多的频率成分在H/V振幅谱比值之后相互抵消而消除. 与FFT结果相比,H/V谱比法计算的结果能有效地简化大楼的振动信号特征,使最主要的振动特征显著化. 因此,利用H/V谱比法能有效地得到结构的自振频率. 与FFT相比,其优点显而易见.
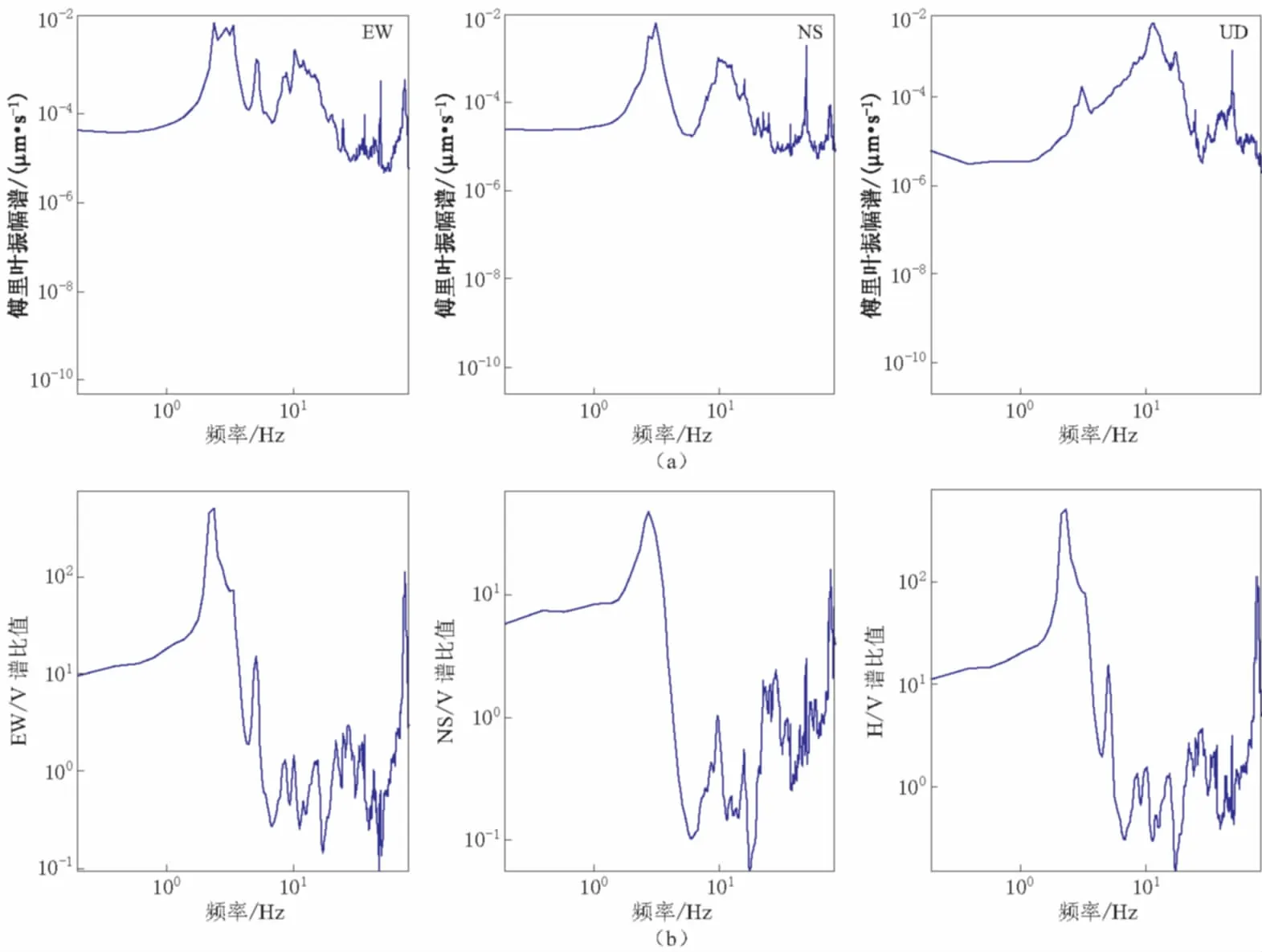
图3 五楼西端三分量速度记录的振幅谱(a)和EW/V、 NS/V和H/V振幅谱比值(b)
图3只给出了一个观测点的记录数据分析结果. 为了更有说服力,我们计算了此次观测系统中所有观测点的数据. 图4给出了大楼西端所有观测点记录信号的EW/V、 NS/V、 H/V振幅谱比值; 图5给出了大楼东端所有观测点记录信号的EW/V、 NS/V、 H/V振幅谱比值. 显然,各层的EW/V、 NS/V振幅谱比值都有一个共同的最为明显的峰值,是2—3 Hz,这是大楼的自振频率. 这说明H/V谱比法能非常准确有效地给出大楼的自振频率. 而且从图上可以看出,随着楼层的增高,这个比值越大,说明楼层越高,建筑结构对振动的放大效应越明显. 另外,还有一个很小的峰值,在5 Hz左右,可能是大楼的扭转频率. 这是由于大楼的东端是自由端,而大楼的西端与一座配楼相连,连接之后呈“L”形. 初步研究表明5 Hz的频率可能是由于地面的扭转运动、 建筑物质量的不均匀分布以及结构刚度计算的局限性等引发的结构扭转振动. 高层建筑结构在地震作用下的扭转振动是难以避免的,平面“L”形高层建筑结构的刚度中心与质量中心偏离更大,扭转也更是难以避免的(沈晓锋等,2002; 马升东等,2005; 蒋俊杰,陈春雷,2008). 这个问题由于本文没有进行专门计算,将在进一步工作中继续研究.
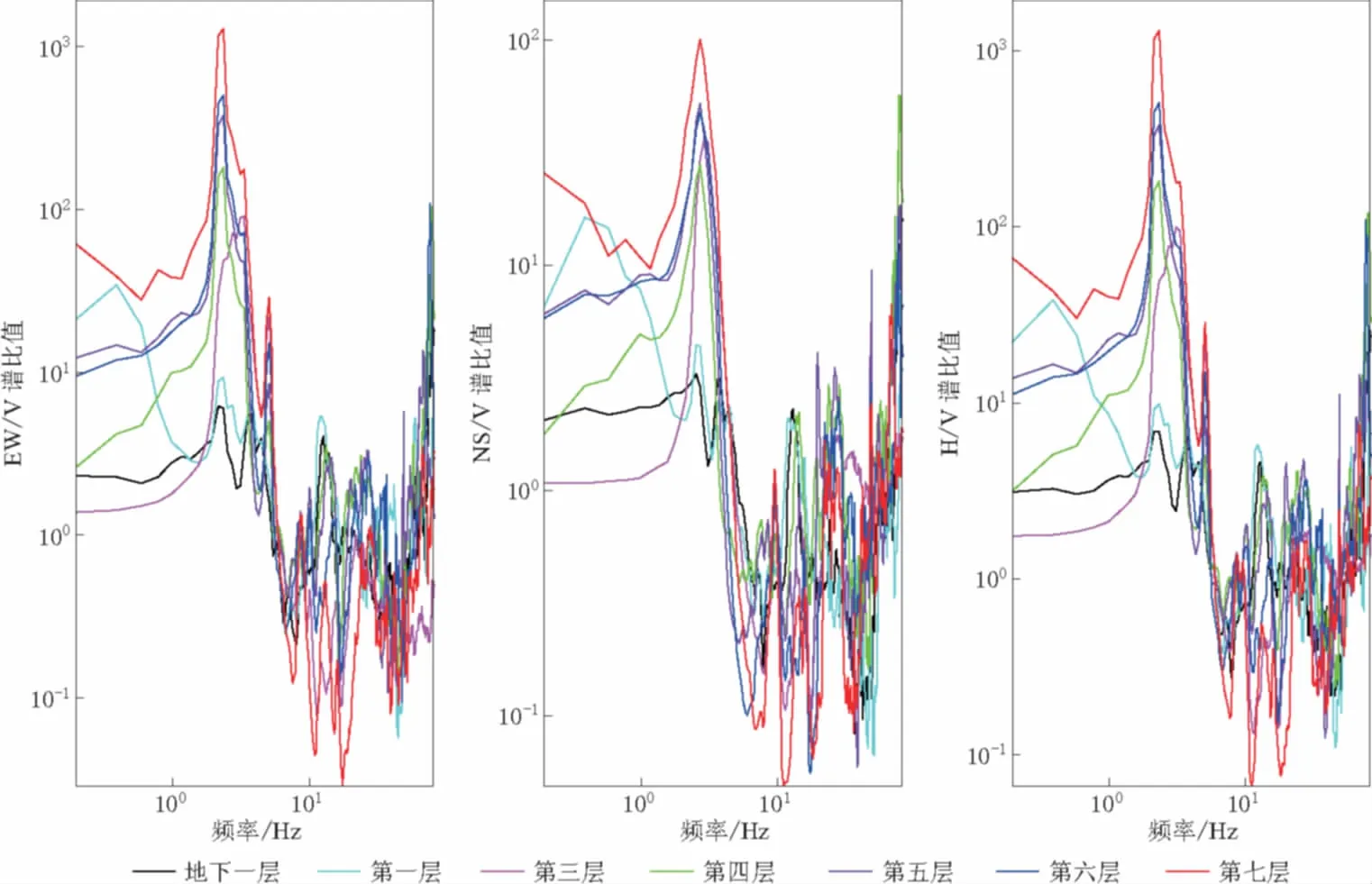
图4 大楼西端各层记录信号的EW/V、 NS/V、 H/V振幅谱比值(第二层数据不能用)

图5 大楼东端各层记录信号的EW/V、 NS/V、 H/V振幅谱比值
2.2 利用H/V谱比法分析结构的放大效应
地震动可以看成不同频率谐波分量的叠加,其作用于同一建筑物时,由于各自频率不同,对应的放大系数也不同,只有与建筑物固有自振频率接近的谐波分量才会得到最大程度的放大; 而相对频率较低的谐波分量基本上维持自身的振幅,比建筑物固有自振频率高的谐波分量可能会削弱. 这种建筑物对不同谐波分量的响应特征,可以理解为建筑物对振动中不同频率成分的选择放大效应. 根据选择放大效应的原理,只有与结构自振频率一致的频率成分会得到最大程度的放大(李洪涛等,2010). 本文利用H/V谱比法,计算水平分量与垂直分量的振幅谱比值,估算结构对振动输入的放大效应.
从EW/V、 NS/V、 H/V谱比值的计算结果可以看到,只有与结构自振频率一致的2—3 Hz得到最大程度的放大,每条谱比值曲线上最高的峰值位置,就是结构的自振频率. 从图4和图5可以看到,在地下一层,也就是结构的基底面,结构对振动的放大比较小,EW/V、 NS/V、 H/V的振幅谱比峰值倍数在3—6之间,但不是1. 因此,对于结构基底面上,根据式(2),HB/VB=SBH/SBV≠1.
对地上1—7层,随着楼层的增加,谱比峰值倍数不断增大,EW分量最大至103量级; NS分量最大至102量级. 这个峰值的位置没有变化,但是谱比峰值倍数逐渐增大. 这说明,楼层越高,结构放大效应越明显. 因此,新建项目,应尽量避免结构自振频率与场地卓越频率的共振,这样可以很大程度地减轻地震灾害. 但是,H/V振幅谱比值的倍数是否就是结构对振动的放大倍数,还有待于进一步分析计算.
2.3 水平向和竖向传递函数
根据式(2),水平分量的传递函数TFH为
(3)
只有当竖向分量的传递函数TFV与结构基底面处的HB/VB谱比值为1时,才能将结构中任一楼层的HS/VS振幅谱比值作为结构水平分量的传递函数,且谱比值表示结构的放大作用. 2.2节中的计算已表明,结构基底面处的HB/VB谱比值不为1. 为了进一步检验HS/VS谱比法结构对振动的放大效应,还需要计算竖向分量的传递函数. 竖向分量的传递函数TFV为
(4)
为了对比研究,同时计算水平分量的传递函数
(5)
式中,SBH和SBV分别为基底面处水平分量和竖向分量的傅里叶振幅谱,SSH和SSV分别为各楼层处水平分量和竖向分量的傅里叶振幅谱.
本文计算了地上1—7层所有楼层的水平(EW、 NS)分量和竖向(V)分量相对与地下一层的传递函数,即SSEW/SBEW,SSNS/SBNS,SSV/SBV(为简单起见,这些比值分别用EW/EWB, NS/NSB, V/VB来表示). 图6和图7分别给出了大楼西端和东端数据的计算结果. 从图中可以看到,不管是EW分量,还是NS分量,只有与结构自振频率一致的2—3 Hz得到了最大程度的放大. 每个楼层的水平分量的传递函数变化很大,而且变化主要集中在结构的自振频率部分. 第一层传递函数的峰值在2—3倍,随着楼层的增高,到第七层时,传递函数的峰值达到了100倍以上. 这表明水平分量的传递函数随着楼层的增高而增大. 但是,竖向分量的传递函数变化不大,尤其是在自振频率部分变化不明显. 对于1—7层,谱比值的变化范围都在1—5之间,但都大于1. 根据式(4),竖向分量的传递函数TFV≠1,而根据式(3),TFH≠HS/VS. 这表明H/V振幅谱比值的放大系数不是结构振动的真实放大系数,H/V谱比法不能真实有效地反映各楼层对振动的放大.

图6 大楼西端各层记录信号的水平向和竖向传递函数(第二层数据不能用)
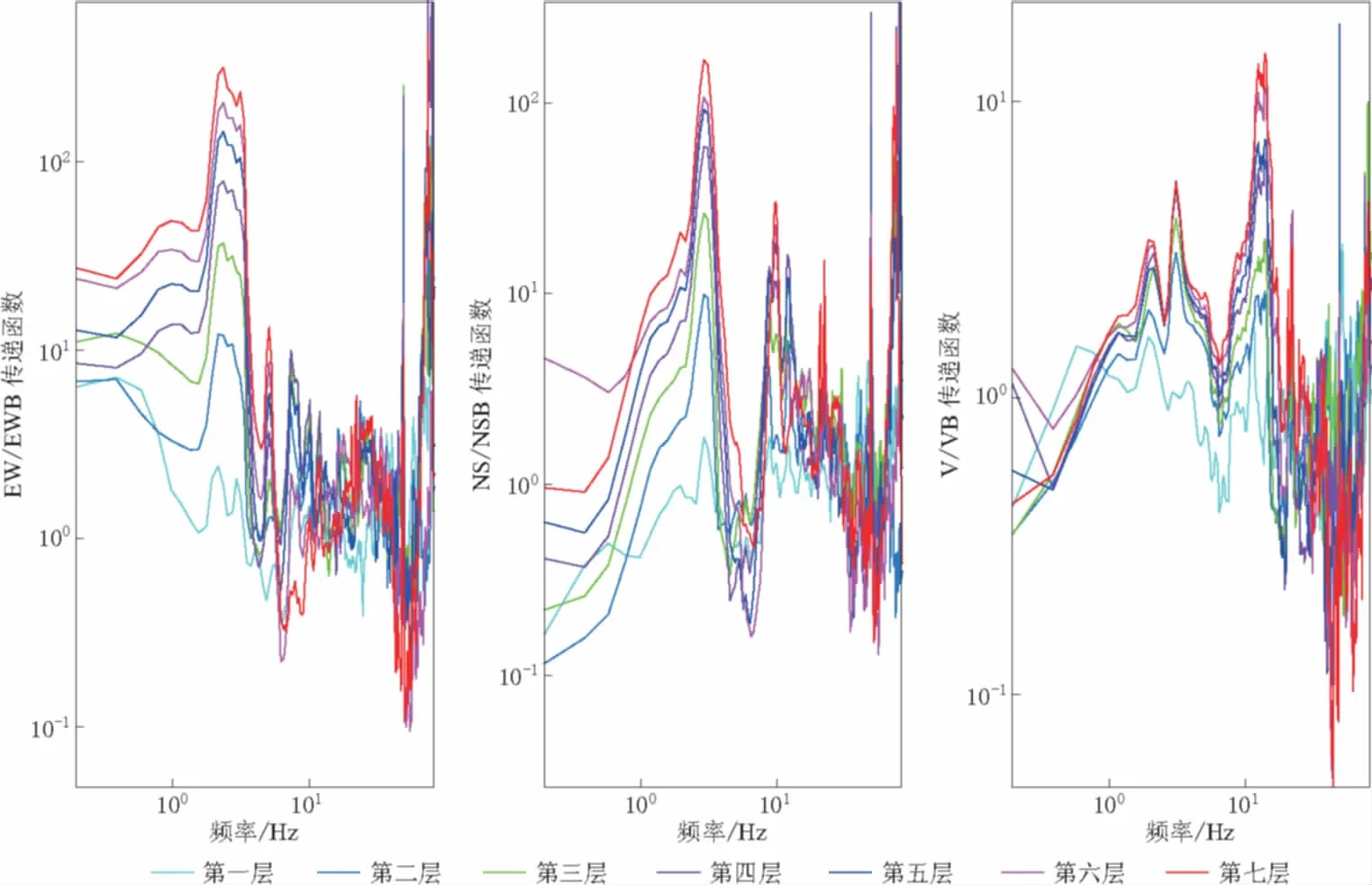
图7 大楼东端各层记录信号的水平向和竖向传递函数
对比图6与图7,发现大楼两端的传递函数非常相似,且对应楼层的放大倍数也非常一致. 但是,大楼西端在2 Hz以下频率范围内的放大,比大楼东端明显. 这可能还是与大楼长条形的矩形结构以及东端与另外一座大楼相连有关. 这一问题将在下一步工作中进行仔细研究.
3 结论
本文以北京城区一栋钢筋混凝土框架结构建筑物内的脉动观测为基础数据,采用H/V谱比法和传递函数法进行计算分析,探讨了中村方法分析结构响应的有效性. 计算分析结果表明:
1) 中村方法在建筑结构中的运用,其原理与在场地土层的运用原理一致. 利用该方法能够有效地得到结构的自振频率.
2) 即使在场地深处的结构基底面处,H/V振幅谱比值也不为1.
3) 随着楼层的增高,H/V振幅谱比值增大. 但是由于竖向传递函数不为1,因此,H/V振幅谱比值不能真实有效地反映各楼层对振动的放大.
4) 水平向传递函数随楼层的增高而增大.
总体看来,采用中村方法,能够有效地得到结构的自振频率,但不能给出结构对振动的放大倍数. 在分析结构响应方面,还是受到一定的限制.
陈棋福,刘澜波,王伟军,Rohrbach E. 2008. 利用地脉动探测北京城区的地震动场地响应[J]. 科学通报,53(18): 2229--2235.
Chen Q F,Liu L B,Wang W J,Rohrbach E. 2009. Site effects on earthquake ground motion based on microtremor measurements for metropolitan Beijing[J].ChineseScienceBulletin,54(2): 280--287.
蒋俊杰,陈春雷. 2008. 高层建筑结构扭转效应控制参数讨论[J]. 广东土木与建筑,(9): 6--8.
Jiang J J,Chen C L. 2008. Discussion on torsional parameters for high-rise building[J].GuangdongArchitectureCivilEngineering,(9): 6--8 (in Chinese).
李洪涛,舒大强,卢文波,朱传云. 2010. 建筑物对爆破振动中不同频率能量成分的响应特征[J]. 振动与冲击,29(2): 154--158.
Li H T,Shu D Q,Lu W B,Zhu C Y. 2010. Building response characteristic to different frequencies of explosive[J].JournalofVibrationandShock,29(2): 154--158 (in Chinese).
梁远森,许红,王云昌. 2005. 高层建筑结构的自振周期的计算与实测[J]. 河南科学,23(5): 699--703.
Liang Y S,Xu H,Wang Y C. 2005. Calculation & actual measurement method on natural vibration period of tall buildings[J].HenanScience,23(5): 699--703 (in Chinese).
卢涛,周正华,周雍年,仲维照. 2006. 关于Nakamura方法有效性的讨论[J]. 地震工程与工程振动,26(1): 43--48.
Lu T,Zhou Z H,Zhou Y N,Zhong W Z. 2006. Discussion on validation of Nakamura’s technique[J].EarthquakeEngineeringandEngineeringVibration,26(1): 43--48 (in Chinese).
罗桂纯,刘澜波,齐诚,陈棋福,陈永平. 2011. 基于地脉动和地铁振动的钢筋混凝土建筑结构响应分析[J].地球物理学报,54(10): 2708--2715.
Luo G C,Liu L B,Qi C,Chen Q F,Chen Y P. 2011. Structural response analysis of a reinforced concrete building based on excitation of microtremors and passing subway trains[J].ChineseJournalofGeophysics,54(10): 2708--2715 (in Chinese).
马升东,周德源,孙良宏. 2005. 平面L形高层建筑的扭转效应分析及对策[J]. 结构工程师,21(1): 10--17.
Ma S D,Zhou D Y,Sun L H. 2005. Torsional analysis and countermeasures for high-rise building with L shape plan[J].StructuralEngineers,21(1): 10--17 (in Chinese).
沈晓锋,季征宇,储诒. 2002. 阶梯形高层建筑的扭转效应分析及对策[J]. 结构工程师,18(3): 1--7.Shen X F,Ji Z Y,Chu Y. 2002. Torsional analysis for ladderlike high-rise building[J].StructuralEngineers,18(3): 1--7 (in Chinese).
Borcherdt R D. 1970. Effects of local geology on ground motion near San Francisco Bay[J].BullSeismolSocAm,60(1): 29--61.
Facke A,Stefano P,Sandra R,Lothar S. 2006. Assessing the vibrational frequencies of the Cathedral of Cologne (Germany) by means of ambient seismic noise analysis[J].NaturalHazard,38(1/2): 229--236.
Gallipoli M R,Mucciarelli M,Castro R R,Monachesi G, Contri P. 2004. Structure,soil-structure response and effects of damage based on observations of horizontal-vertical spectral ratios of microtremors[J].SoilDynEarthqEng,24(6): 487--495.
Nakamura Y. 1989. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface[J].QRepRailwayTechResInst,30(1): 25--33.
Discussion on validity of structural response by Nakamura’s technique

1)InstituteofGeophysics,ChinaEarthquakeAdministration,Beijing100081,China2)EarthquakeAdministrationofBeijingMunicipality,Beijing100080,China3)DepartmentofDisasterPreventionEngineering,InstituteofDisasterPrevention,HebeiSanhe065201,China
A method called Nakamura’s technique, which uses a horizontal-to-vertical Fourier spectrum ratio (H/V ratio) of microtremor to estimate the dynamic characteristics of a site, was introduced by a Japanese scholar Nakamura in 1989. This technique is widely used, and fruitful achievements in scientific research are presented by this technique. Nowadays, this technique is also used to estimate the structural response characteristics by home and abroad researchers. However, the validity of Nakamura’s technique is still in dispute. The ambient seismic noise measurement was conducted inside a reinforced concrete (RC) building in urban area of Beijing. The calculative analysis on velocity data by Nakamura’s technique is done. The analyses indicate that the natural frequency can be obtained validly by the Nakamura’s technique, but the magnification is not accurate. We must use this technique to estimate structural response characteristics carefully, and we suggest other methods should be used simultaneously to compare.
Nakamura’s technique; H/V ratio; structural response; validity
10.3969/j.issn.0253-3782.2014.03.014.
北京市地震局任务性科技专项(JZX-201205)资助.
2013-04-15收到初稿,2013-09-09决定采用修改稿.
e-mail: gchluo@163.com
10.3969/j.issn.0253-3782.2014.03.014
P315.9
A
罗桂纯,李小军,王玉石,卢滔. 2014. 关于中村(Nakamura)方法分析结构响应有效性的讨论. 地震学报, 36(3): 491--499.
Luo G C, Li X J, Wang Y S, Lu T. 2014. Discussion on validity of structural response by Nakamura’s technique.ActaSeismologicaSinica, 36(3): 491--499. doi:10.3969/j.issn.0253-3782.2014.03.014.

