基于改进RBF的空间插值算法及其在矿体三维可视化中的应用

周仲礼, 马 腾, 陈秀荣, 秦飞龙

(数学地质四川省重点实验室,成都 610059)

基于改进RBF的空间插值算法及其在矿体三维可视化中的应用

周仲礼, 马 腾, 陈秀荣, 秦飞龙

(数学地质四川省重点实验室,成都 610059)

为径向基神经网络确定更为优化的初始中心，增强径向基网络的性能。通过采用改进的模拟退火蚁群算法作为径向基神经网络径向基层的训练法，将改进的径向基神经网络模型应用于地层高程的面插值和矿体品位的空间体插值，并与普通克里金法进行交叉验证，优化效果明显，然后利用VC++与OpenGL开发环境开发出矿体可视化系统，结果在结合矿体实际数据进行实例应用的过程中，实效性明显。

矿体品位预测;改进的模拟退火蚁群径向基;地层面插值;空间插值

在矿业资源开发生产项目中，矿体的品位预测及储量估算是矿业公司的首要需求。而要满足这些需求，首要的是要通过采样点数据分析出矿体的分布规律。然而，受制于项目经费有限等客观因素，采样点数据的数量显然不足以全面反映矿体的分布情况。因此，采用空间插值技术来弥补采样点数据信息的不全面就理所当然地成为一种有效的方法。如克里金法和其衍生出的趋势克里金法[1]，协同克里金法[2,3]和平滑修正克里金法[4]等。然而，从本质上讲，它们都属于依据线性理论的滑动加权平均的方法，因此在局部易造成因对数据进行平滑操作而引起的信息遗失；另外，其对具有非线性特征的矿体品位空间分布的描述在精度上也存在一定的限制。而且使用克里金类方法是有前提条件的，它要求插值变量满足本征假设或平稳假设，采样数据服从对数正态分布或正态分布。这样的要求在现实中显然是难以达到的。因此，寻求一种对非线性系统处理能力强大又对采样数据分布和假设没有要求的方法尤为迫切和重要。而本文提出的径向基神经网络插值法正是这样一种方法，但美中不足的是径向基神经网络很难确定合理而有效的中心。针对这一难题，本文将蚁群和模拟退火算法进行全新结合形成一种有效的优化方法，并以此作为径向基网络径向基层的新训练方法来确定更为优化的网络中心，从而很好地解决了这一难题，形成了一个改进模拟退火径向基空间插值的全新模型，为更精确合理地进行矿体空间品位插值提供了一种新的思路，而且具有实效性。同时利用VC++和OpenGL相结合的环境从底层实现了此新模型下的矿体可视化系统的开发，从而使用户可以更为直观和便捷地分析和了解矿体内部品位分布状况。

1 算法模型

从理论上讲，神经网络虽然适合处理非线性系统的问题，但是由于矿体形成外因是复杂的地质变化过程，再加上所能提供的采样数据是极其有限的，所以仅仅依据有限的采样数据去拟合整个矿体品位如此复杂的超曲面显然是十分困难的。也就是说选用整体内插的思路是不易实现的。除此之外常用的内插方法还有逐点内插法和分块内插法。其中逐点内插法顾名思义即可知其过程繁琐，因此实效性不强。而与其相对的分块内插法不但实现过程简便，而且由于将矿体品位数据进行分类处理而降低了整体复杂度。所以分块内插法是首选。

而RBF网络即是一种分块内插方法。首先其径向基层对样本数据进行分类，再分别对每类数据进行训练。这样等同于将原本十分复杂的问题分为若干相对不复杂的问题分别解决，可行性显然更高。然而RBF网络受制于初始中心难确定和解决复杂问题时隐含层节点过多的困境。本文采用新的模拟退火与蚁群相结合的算法来为RBF网络确定更为优化的初始中心，从而减少了冗余的隐含层节点，有效改善了这种局面。

径向基神经网络分为3层：输入层、隐含层和输出层。不同于BP神经网络，径向基网络采用局部连接，训练收敛速度更快；而且训练方式采用分部训练方法，先训练第一层径向基层权值，再训练输出层权值。对于本文采用的空间插值模型，设置输入层神经元节点数为3，分别对应空间的(x,y,z)坐标值。输出层的节点数为1，对应矿体品位值。隐含层选用激励函数radaps(x)=exp(-x2),输出层选用线性函数，将隐含层的输出与输出层权值加权求和作为网络输出。径向基网络径向基层的训练原理其实是一种聚类过程，而正是由于其各类初始中心确定的困难严重制约径向基网络的性能。这种聚类过程可看做是TSP问题中的寻优问题，解决这类TSP问题常用的算法有蚁群算法和模拟退火算法，且它们在寻优能力上各有优劣。模拟退火在无限长马氏链条件下理论上可保证以概率收敛于全局最优解，但计算时间过长。而蚁群算法虽然收敛速度较快，但易陷入局部最优。所以将两者巧妙地结合可以互补短板。

本文提出的结合方法的主体思路是，外部循环采用模拟退火算法的模型思路以便最终收敛于全局最优解，内部循环采用蚁群算法的模型思路以保证收敛速度。且收敛条件相互制约，从而增强了新模型的实效性。

其中蚁群算法的主要思路是：将径向基层的权值和阈值所组成的n个数记为qi。每个qi的可能值设为m个非零随机数，记为集合Iqi。令蚁群中所有蚂蚁都走遍这n个集合，其中每个蚂蚁在每个集合中选择一个元素，而选择每个元素的概率由元素对应的信息素来控制。这样一只蚂蚁的全部选择就确定了一组径向基层的参数。然后不断地更新每个元素的信息素来控制蚂蚁再次选择的概率。

为防止蚁群算法过早收敛陷入局部最优，本文将模拟退火算法的控制温度T设为初始值为1向0衰减的变量，有别于蚁群算法中信息素挥发系数的多种改进方法，本文将控制温度T作为信息素挥发系数ρ。这样就保证了初始温度较高时选择每个参数的概率差别不是很大，即扩大了可选空间，经大量验证其可有效防止过早收敛。

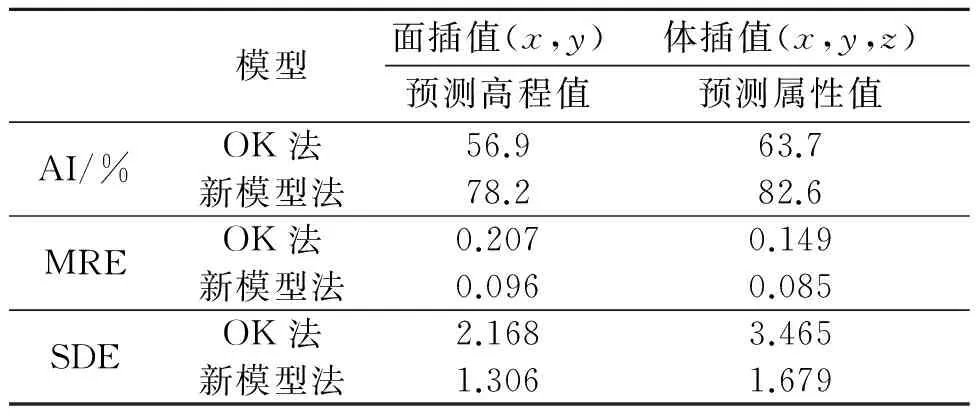
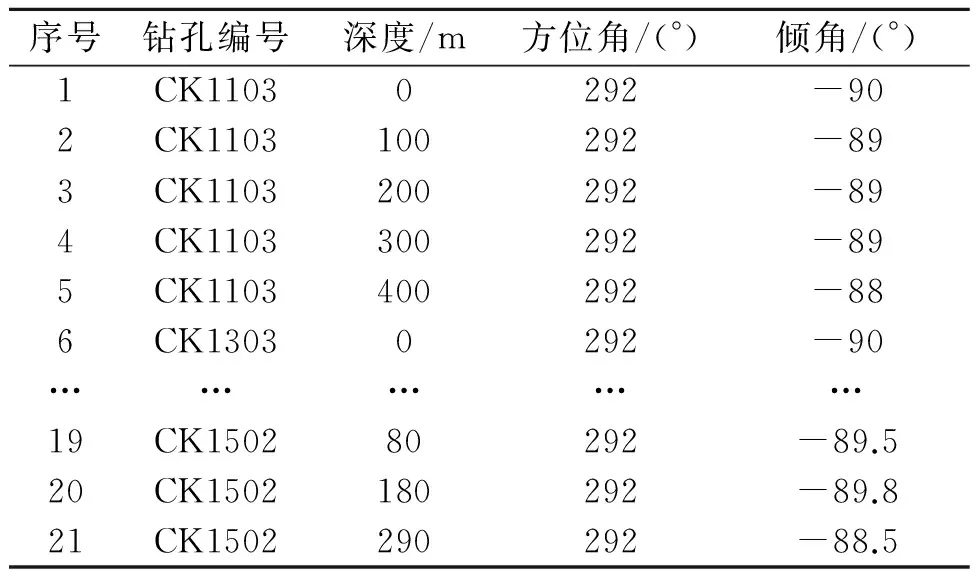
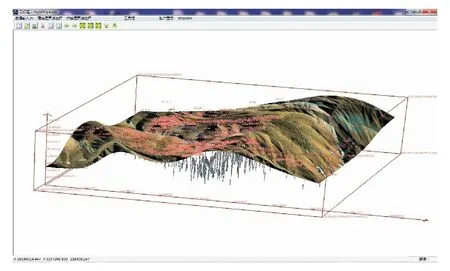
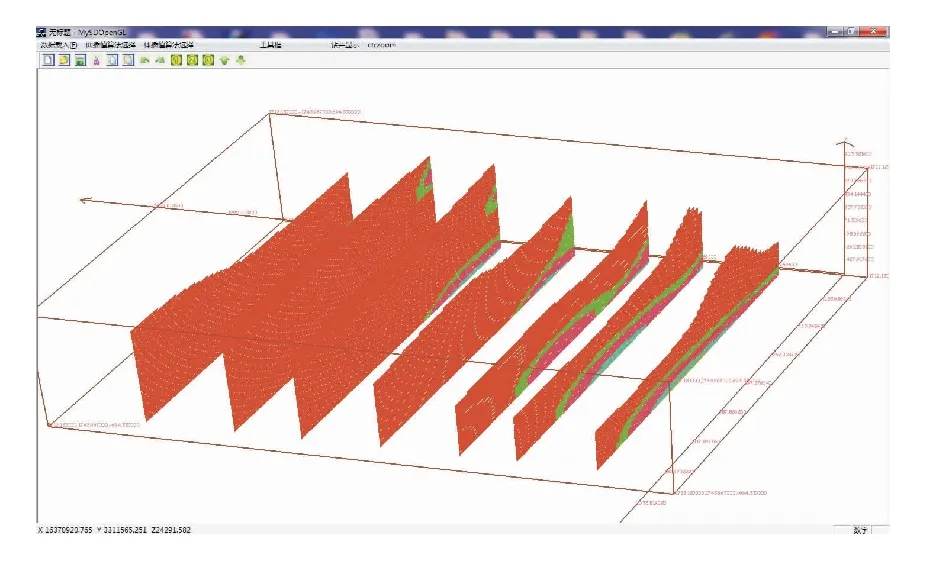
同时对改变每个元素信息素的条件作了限制，设定一个目标误差goal，对每次蚁群选择的所有解中选出最优解ymax，并算得其对样本的最大输出误差Emax。当此次Emax小于前次Emax时，就接受这次选择的所有解，按规则改变元素信息素；否则按模拟退火算法中对新解的接受概率来接受新解。当蚁群停滞于若干解时，进行降温处理并记录此时解的个数和所有解的最大误差Esmax，从而提高了信息素对选择概率的影响使解的范围更集中。当相邻两次降温处理记录的解数相同且每组解的最大误差和Esmax

a.蚁群数量设为常数h，目标输出误差goal=0.01；外层降温循环次数记为Ndc，初始化为0；最大降温循环次数为Nmc；内层循环次数记为Nc，也初始化为0。设每个元素j的信息素为Tj(Iqi)=1，令改变量ΔTj(Iqi)=0，初始温度T0=1，温度改变系数α=0.1。

b.让所有蚂蚁在各集合中选元素，则第k只蚂蚁选择第i个集合的第j个元素的概率

(1)

所有蚂蚁选择好各自的一组元素后，令Nc=Nc+1。

c.记录蚁群选择的解的个数为NI，计算每组解对样本训练的最大输出误差，记录所有解中最优解ymax(Nc)和最优解对应样本的最大输出误差Emax(Nc)。设r为区间[0,1]上服从均匀分布的随机数，且记

Δf=Emax(Nc)-Emax(Nc-1)

激光多普勒测速仪以其测速精度高、动态响应快、空间分辨率高等优点，广泛应用于航空、航天、交通等领域，也可用于卫星间的通信，测距等应用中[1-4]。激光多普勒测速仪大多直接利用激光的多普勒效应来获取目标速度，激光的多普勒频移较大，待测速度为1 m/s时，多普勒频率就能达到兆赫兹量级，当待测速度达1 000 m/s以上时，多普勒频移将超过108Hz，极大增加了测速系统的信号处理难度[3]。

(2)

而接受概率

P(TNdc)=e(-Δf/TNdc)

(3)

同时记

Tj(Iqi)(Nc)=(1-ρ)Tj(Iqi)(Nc-1)+ ΔTj(Iqi)

(4)

其中ρ为信息素挥发系数，且令ρ=TNdc，均是区间[0,1]上按一定规律变化的数。

(5)

(6)

d.判断当NI(Nc) =NI(Nc-1)且Emax(Nc)=Emax(Nc-1)时跳到(e)，且记录此时所有解的最大输出误差和Esmax(Ndc)，解的个数为NI(Ndc)；否则跳到(b)。

e.当Ndc=Nmc或NI(Ndc)=NU(Ndc-1)且Esmax(Ndc)

f.否则令Ndc=Ndc+1，TNdc=(1-α)TNdc，Nc=0。然后跳(b)。

g.去掉多余的重复结点，重新设定RBF层的结点数，通过文献[9]的改进的共轭梯度法训练输出层权值。

技术流程如图1。

2 实证研究与应用

2.1 实例检验

以矿山勘察的钻井数据作为原始采样数据，将构成钻井数据的井口数据表、测斜数据表和品位数据表导入。依据文献[10]的方法对原始数据进行离散化处理，将原始线性数据转化为插值所需要的空间离散数据。对离散化后的样本数据进行归一化处理，选取其中276组数据为训练样本，另外25组为测试样本。先选用普通克里金即OK法进行插值，接着利用新模型结合离散化后的采样数据分别进行地表的面插值和矿体品位的空间体插值。首先结合改进的蚁群算法来确定RBF的网络结构。由于模型用作空间插值，所以输入层神经元结点数设定为3，隐含层初始设定为276，输出层神经元为1。经改进的蚁群算法聚类后，得到新的聚类中心数为11，则重新调整隐含层节点数为11。然后选用改进的共轭梯度法，通过训练样本训练输出层权值。最后经测试样本插值得到结果与OK法插值结果对比如表1(部分经平移处理)。

图1 算法流程设计图Fig.1 Algorithm process design

表1 测试结果验证对比Table 1 Contrast of test results

采用相同模式，利用井口数据提供的面差值训练样本训练网络，并进行面插值。在比较新模型与OK法的插值精度时，本文采用插值精度AI(accuracy of interpolation),相对误差平均值MRE(mean of relative error)和预测误差的标准差SDE(standard deviation of prediction error)这3个指标来评价。AI反映的是预测值和真实值之间偏差的大小，AI值越大代表它们之间的误差越小；MRE反映的是预测值相对真实值的偏差度；SDE反映的是偏差的波动程度。它们的公式如下。

(7)

(8)

表2 插值验证结果精度统计Table 2 The statistics of accuracy of interpolation verification results

由表2可知，无论是对高程进行的面插值，还是对品位进行的体插值，新模型法对高程和属性值的插值精度都比OK法有明显提高。进行面插值时，输入相同的变量(x,y)，新模型的插值精度AI提高了37.4%，MRE和SDE分别降低了53.6%和39.8%；同理，进行体插值时，输入相同变量(x,y,z)，由表中数据计算知，新模型的AI提高了29.7%， MRE和SDE分别降低了42.9%和51.5%。 即两种插值情况下，新模型法相对于OK法在插值精度明显提高的同时，偏差度和偏差的波动程度也均有显著降低；但是如果要追求得到更高效果，需要的训练时间会成倍增加，因此在实际应用中，需要设定一个时间和精度的范围。此结论表明新模型法的插值效果在一定时间和精度要求范围内明显优于OK法，具有很强的实效性。

2.2 实例应用

基于新模型的插值方法，结合矿山勘探实际需求，利用VC++和OpenGL环境开发出矿体可视化系统。为方便进行传统储量估算，本文采用块段体模型的建模思路。首先通过与用户交互的方式确定采用的网格尺寸。将勘探钻孔的见矿点及地表DEM和此区域的遥感影像共同进行可视化。同时利用视图变换、模型变换、投影变换、视口变换和模拟变换来实现平移、旋转、放缩及精确定位等功能，结合设定合适的光照和材质实现真实的三维场景。利用空间品位插值的结果结合用户设定和选择的品位区间进行矿体三维可视化，在平移、放缩、旋转和定位功能的基础上增加和用户相交互的剖切功能，从而可得到不同矿体在不同地层的切片，方便更进一步了解矿体内部品位的空间分布情况。

结合某研究区铜矿勘探数据的井口数据表、测斜数据表和品位数据表(其中部分测斜数据表如表3)，进行离散化处理，然后通过用户提供的网格尺寸信息利用新模型分别进行地表的面插值和品位的体插值，得到钻孔工程三维可视化效果图(图2)。结合用户设定和选择的品位区间进行矿体可视化(图3)。利用OK模型进行品位的体插值，结合用户设定和选择的品位区间进行矿体可视化(图4)。结合用户定位交互对矿体进行剖切处理，得到不同地层的品位分布切片图(图5)。对矿区的高程进行颜色区分得到的高程DEM图(图6)。最后依据采样信息及矿体品位插值结果可估算插值区域矿体储量。

表3 测斜数据Table 3 Survey data

图2 钻孔工程三维可视化Fig.2 3D visualization of the drilling engineering

图3 新模型矿体可视化的品位分布显示Fig.3 The new model of the grade distribution of the ore body visualization

图4 OK模型矿体可视化的品位分布显示Fig.4 OK model according to the grade distribution of the ore body visualization

图5 地层的品位分布切片Fig.5 Grade distribution of the stratigraphic section

图6 矿区的高程DEMFig.6 The elevation of DEM in the mining area

3 结束语

通过交叉验证可以发现，新模型在插值效果上明显好于传统的克里金法。通过对湖北铜绿山铜铁矿床的铜矿数据进行的实例应用，可以体现出依据新模型开发出的矿体可视化软件实效性明显，对用户进一步对矿体的开发提供直观便捷的帮助。当项目经费有限等客观因素限制了采样点数据的数量，导致不足以全面反映矿体的分布情况时，采用新模型开发的矿体可视化软件，完全可以在要求精度内完成矿体的品位预测及储量估算工作，具有继续研究及拓展应用的价值。

[1] 徐英，王俊生，蔡守华，等．缓坡水平梯田土壤水分空间变异性[J]．农业工程学报，2008, 24(12)：16-19． Xu Y, Wang J S, Cai S H,etal. Soil water spatial variability of gentle slope level terrace[J]. Journal of Agricultural Engineering, 2008, 24(12): 16-19. (In Chinese)

[2] 李元寿，王根绪，丁永建，等．青藏高原高寒草甸区土壤水分的空间异质性[J]．水科学进展，2008,19(1)：61-67. Li Y S, Wang G X, Ding Y J,etal. Qinghai-Tibet plateau alpine meadow area spatial heterogeneity of soil moisture[J]. Advances in Science Water, 2008, 19(1): 6l-67. (In Chinese)

[3] Wu C F, Wu J P, Luo Y M,etal. Spatial estimation of soil total nitrogen using Cokriging with predicted soil organic matter content[J]. Soil Sci Soc Am J, 2009, 73(5): 1676-1681.

[4] 杨雨亭，尚松浩，李超．土壤水分空间插值的克里金平滑效应修正方法[J]．水科学进展，2010，21(2)：208-213. Yang Y T, Shang S H, Li C. Soil moisture spatial interpolation and the smooth effect correction method[J]. Advances in Science Water, 2010, 21(2): 208-213. (In Chinese)

[5] Skaf Z, Wang H, Guo L. Fault tolerant control based on stochastic distribution via RBF neural networks[J]. Journal of Systems Engineering and Electronics, 2011, 22(1): 63-69.

[6] Wang H, Afshar P, Yue H. ILC-based generalised PI control for output PDF of stochastic systems using LMI and RBF neural networks[C]//Proc of the IEEE Conference on Decision and Control. San Diego: IEEE, 2006: 5048-5053.

[7] 李冰,刘洪,李幼铭.三维地震数据离散光滑插值的共轭梯度法[J].地球物理学报，2002(5):691-699. Li B, Liu H, Li Y M. Discrete smooth interpolation with 3D seismic data of the conjugate gradient method[J]. Journal of Geophysics, 2002(5): 691-699. (In Chinese)

[8] 陈冬花, 邹陈, 王苏颖,等.基于DEM 的伊犁河谷气温空间插值研究[J].光谱学与光谱分析，2011(7):1925-1929. Chen D H, Zhou C, Wang S Y,etal. Based on the DEM of the ili river valley temperature spatial interpolation research[J]. Spectroscopy and Spectral Analysis, 2011(7): 1925-1929. (In Chinese)

[9] 马腾，周仲礼，陈秀荣,等.基于改进共轭梯度BP法的化探矿床预测系统开发[J].软件, 2012(11):81-84. Ma T, Zhou Z L, Chen X R,etal. Based on the improved conjugate gradient back propagation BP method of geochemical prospecting for ore deposits prediction system development software[J]. Software, 2012(11): 81-84. (In Chinese)

[10] 刘亚静，李梅，姚纪明.三维普通克立格插值建立非层状矿体块段模型的研究[J].金属矿山, 2008(7):92-99. Liu Y J, Li M, Yao J M. The research of three dimensional ordinary Kriging interpolation to establish the layered orebody block segment model[J]. Metal Mine, 2008(7): 92-99. (In Chinese)

Spatial interpolation algorithm based on improved RBF and its application to orebody 3D visualization

ZHOU Zhong-li, MA Teng, CHEN Xiu-rong, QIN Fei-long

GeomathematicskeyLaboratoryofSichuanProvince,Chengdu610059,China

The improved simulated annealing ant colony algorithm is used as the radial basic training method of RBF neural network. Its more optimization determines the initial center for radial basis neural network and enhance the performance of the radial basis network. The improved RBF neural network model has been applied to the stratigraphic vertical surface interpolation and orebody spatial interpolation, and verified crossly with the ordinary Kriging method, and the optimized effect is obvious. Then, the ore body visualization system developed by VC++and OpenGL development environment software is used. The result shows that in the application of the example combined with the actual data of the orebody, the effectiveness is very obvious.

ore grade prediction; simulated annealing ant colony radial basis; level interpolation; spatial interpolation

10.3969/j.issn.1671-9727.2014.05.15

1671-9727(2014)05-0645-06

2013-08-21 [基金项目] 国家自然科学基金资助项目(41272363)

周仲礼(1971-),男，博士，教授，从事应用数学的教学与科研工作， E-mail:zzl@cdut.edu.cn。

TP319:P628

A