一种瞬时谐波参数估计的新方法

吕干云，吴传满，吴育聪，李军

（1.南京工程学院电力系，南京210014；2.浙江师范大学数理信息学院，金华321004）

一种瞬时谐波参数估计的新方法

吕干云1，2，吴传满2，吴育聪2，李军1

（1.南京工程学院电力系，南京210014；2.浙江师范大学数理信息学院，金华321004）

为解决动态谐波的瞬时参数估计问题，提出了一种瞬时谐波参数估计的新方法。假定信号的各谐波分量都分布在有限频带内，通过该信号卷积相应频带理想带通滤波器的冲激响应，即可得到信号的滤波输出，将各带通滤波器输出在零频率处展开，就能得到对应谐波分量的瞬时参数，从而实现该多分量信号的瞬时谐波参数估计。算例结果表明，该法能较好地完成动态谐波的瞬时振幅、频率估计，并具有良好的精度、实时性。

带通滤波器；多分量信号；瞬时谐波；参数估计；谐波分量

随着国民经济的飞速发展，冶炼、电气机车、矿业的冲击负荷和各类非线性负荷被广泛使用，各种大型用电设备的启停导致交流电网中电压和电流波形严重失真[1]，给电力系统带来很大的危害。研究有效的瞬时谐波参数估计算法成为近年来的研究热点，瞬时谐波参数估计为电力谐波抑制与补偿提供科学依据[2]。

在电力谐波参数估计中，快速傅里叶变换FFT（fast Fourier transform）具有运算简单和计算效率高的特点，但傅里叶变换存在栅栏效应和泄漏现象[3]，在信号参数估计中存在较大误差。为减小频谱泄漏的影响，采用加余弦窗双插值FFT算法来分析间谐波[4]，提高谐波分析的准确性；文献[5]提出改进傅里叶变换的瞬时参数估计算法，采用傅里叶变换的翘曲时间信号，将翘曲算子限定在一个连续时间翘曲的二阶多项式映射中，有效地实现了瞬时谐波参数的估计，但该方法只适用于振幅不变的线性频率估计；文献[6-7]提出Hilbert变换处理非平稳信号的算法，能精确估计瞬时谐波参数，但是变换前先必须将信号通过经验模态分解成固有模态函数分量，同时经验模态分解过程中存在边界效应及模态混叠和虚假模态等缺点。处理非平稳信号算法还有最小二乘法[8]、卡尔曼滤波法[9]、离散能量分离算法[10]、小波变换[11-12]、小波包[13]、Newton法[14]和WVD的时频分布[15]等。

本文提出了一种瞬时谐波参数估计的新方法，通过信号卷积相应频带理想带通滤波器的冲激响应得到信号的带通滤波输出，然后将各带通滤波器输出在零频率处展开得到对应谐波分量的瞬时参数，能对谐波振幅变化、频率变化、振幅频率同时变化等多分量信号进行有效的参数估计，瞬时性很好。

1 非平稳信号瞬时谐波参数估计算法

在正弦模型[16]的基础上，假定被分析信号s（n）的每一个谐波分量在频域中都分布在有限的窄带频带内，所有谐波分量可由没有频谱混迭的滤波器组完成分离。通过该信号卷积相应理想带通滤波器的冲激响应hk（n），得到该带通滤波器的输出信号sk（n），然后对各带通滤波器输出信号在零频率处展开，得到对应谐波分量的瞬时参数，实现多分量非平稳信号的瞬时谐波参数估计。算法定义的谐波数目L和频率边界为：F0≤F1≤…≤FL，其中，F0=0，FL=（FS/2）。则被分析信号s（n）为

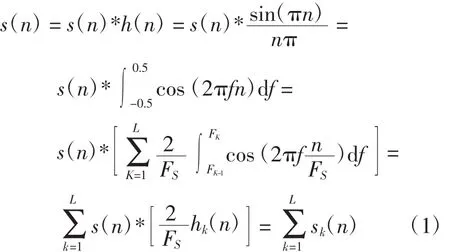
式中：hk（n）为带通滤波器在频带[FK-1，FK]的冲激响应；sk（n）为带通滤波器的输出信号。其中，hk（n）为

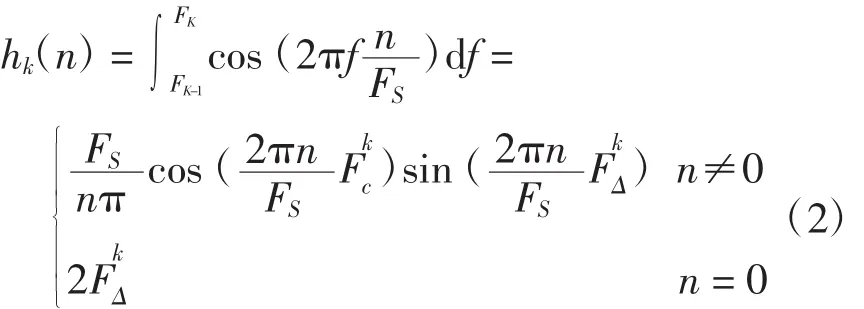
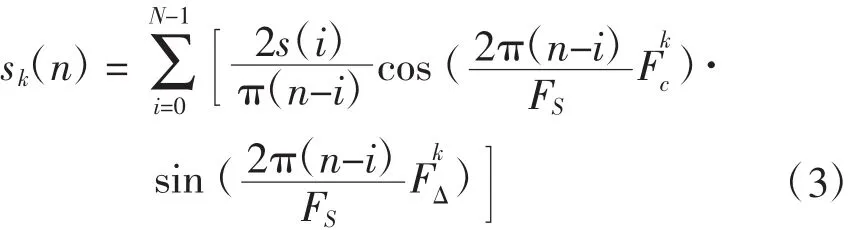
式（3）改写为

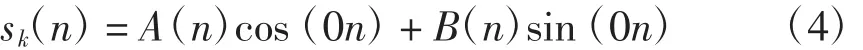
其中：

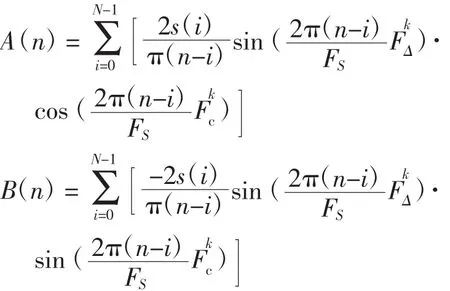
将式（4）变换，得

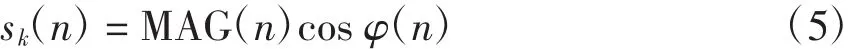
其中，瞬时振幅MAG（n）、瞬时相位φ（n）和瞬时频率f（n）分别为

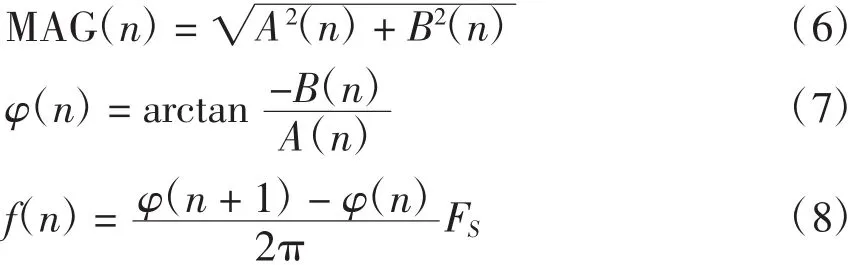
可以实现多分量非平稳信号的瞬时谐波参数估计。

2 算例分析

采用多分量非平稳信号的模型为

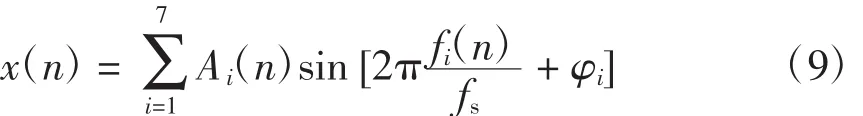
式中：i为谐波次数；Ai（n）、fi（n）分别为第i次谐波在n时刻的瞬时振幅、频率；φi为谐波初相位。基波频率f1为50 Hz，采样频率fs为3 197 Hz；数据长度N取1 280点。在1台CPU2.66 GHz、内存2.0GB的Dell PC机上进行仿真，并采用Matlab 2008软件。基波及各次谐波参数如表1所示。

2.1 振幅变化的瞬时谐波参数估计

算例中各谐波频率不变，f5（n）=250，f7（n）=350。5次、7次谐波振幅瞬时变化，A5（n）=1+|cos n|，A7（n）=1-0.05|cos t|，结果见图1和表2。

由图1、表2可知，5次、7次谐波参数估计具有很好的实时性，能快速跟踪谐波振幅的瞬时变化。其中，5次谐波振幅估计仅在瞬变处存在较大相对误差（6.0%），其他采样处相对误差都在2.0%以下；7次谐波振幅估计在始末阶段相对误差在2.00%，在稳定阶段保持相对误差在0.30%；5次谐波频率估计相对误差为0.20%；7次谐波频率估计相对误差为0.40%。算法对其余各次谐波的参数也有较高的估计精度。

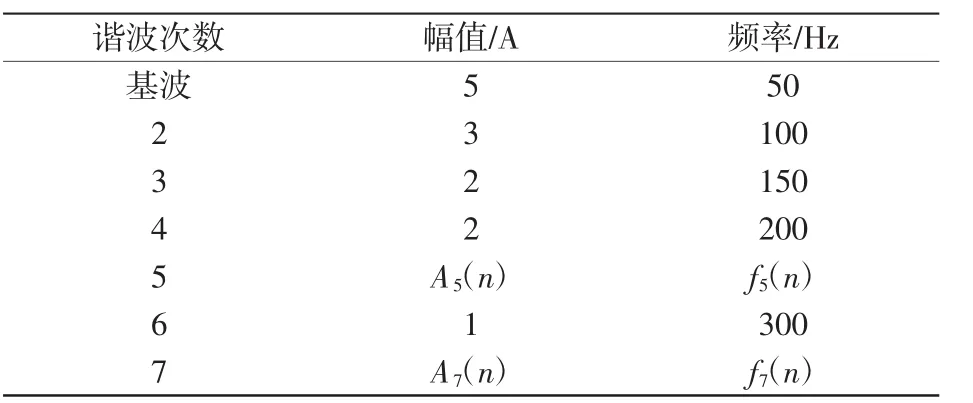
表1 信号谐波参数设置Tab.1Settings of signal harmonic parameters

图1 振幅变化下5次、7次谐波的瞬时参数估计Fig.1Instantaneous parameters estimation of 5th and 7th harmonics with amplitude-variant signals

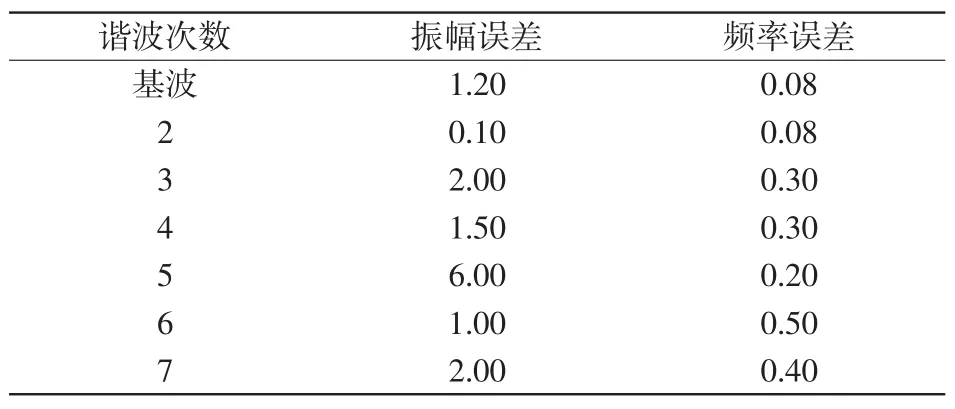
表2 各次谐波参数的估计误差Tab.2Estimation errors of harmonic parameter %

2.2 频率变化的瞬时谐波参数估计

算例中信号各谐波分量的振幅不变。5次、7次谐波频率瞬时变化，结果见图2和表3。

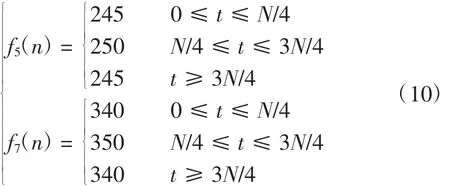
图2和表3的结果表明，5次、7次谐波估计参数具有很好的实时性，能快速跟踪谐波频率的瞬时变化。其中5次谐波频率估计仅在瞬变处存在较大相对误差1.10%，其他处相对误差都在0.20%以下；7次谐波频率估计在瞬变处相对误差为1.50%，其他各处相对误差都在0.30%以下；5次谐波振幅估计相对误差保持在2.00%；7次谐波振幅估计相对误差约为6.00%。算法对其余各次谐波的参数估计也有较高的精度。

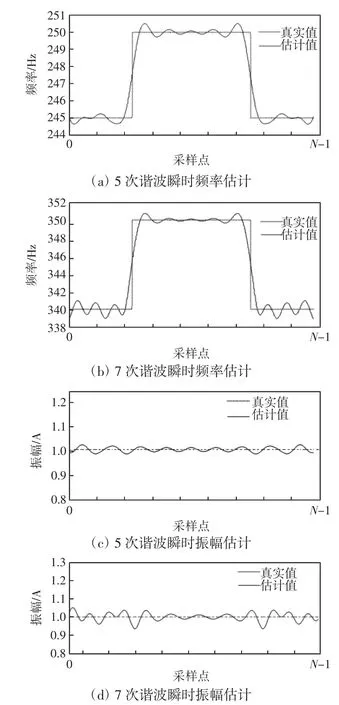
图2 频率变化下5次、7次谐波的瞬时参数估计Fig.2Instantaneous parameters estimation of 5th and 7th harmonics with frequency-variant signals

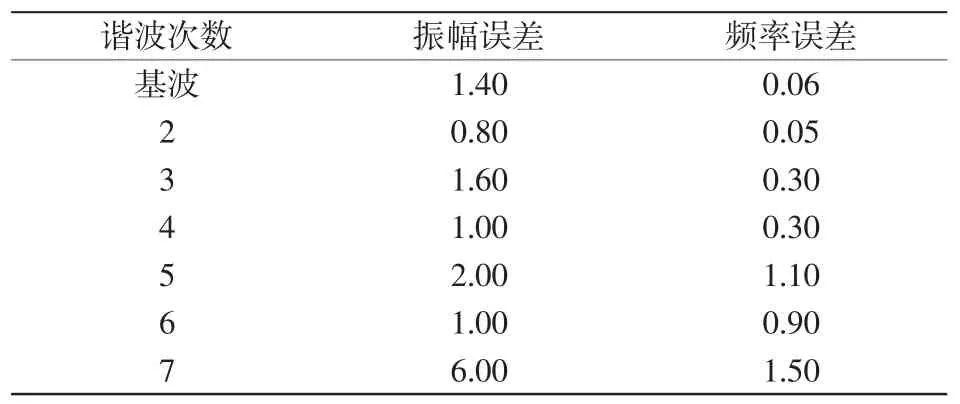
表3 各次谐波参数估计误差Tab.3Estimation errors of harmonic parameter %

2.3 振幅频率同时变化

算例中信号各谐波分量参数见表1。其中5次、7次谐波频率、振幅瞬时变化如下：f5（n）、f7（n）见式（10）；A5（n）=1+|cosn|，A7（n）=1-0.05|cost|。结果如图3和表4所示。

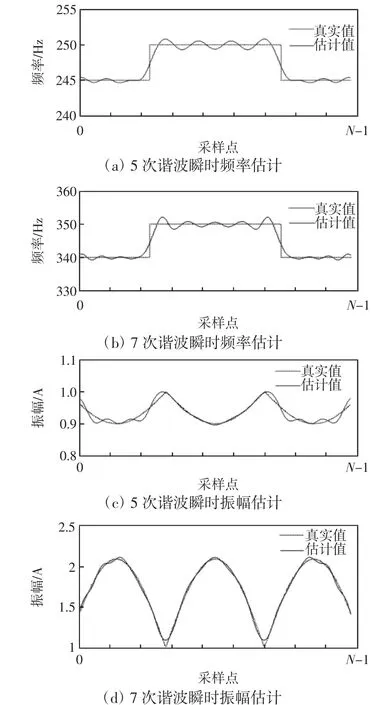
图3 振幅频率变化下5次、7次谐波的瞬时参数估计Fig.3Instantaneous parameters estimation of 5th and 7th harmonics with amplitude-variant and frequencyvariant signals

表4 各次谐波参数估计误差Tab.4Estimation error of harmonic parameters %

图3和表4仿真结果表明，5次、7次谐波参数估计具有很好的实时性，能快速跟踪谐波振幅和频率的瞬时变化。图3（a）表明，5次谐波估计频率仅在瞬变处存在较大相对误差1.2%，其他各采样处都约为0.2%；图3（b）表明，7次谐波估计频率仅在瞬变处存在较大相对误差1.5%，其他各采样处都在0.5%以下；图3（c）表明，5次谐波估计振幅相对误差为2.0%左右；图3（d）表明，7次谐波估计振幅除了在瞬变处存在较大相对误差，为8.0%，其他各采样处相对误差都为2.0%左右。算法对其余各次谐波的参数估计也具有较高精度。

3 结语

随着电力系统中的非线性负荷大量增加，大量的谐波和次谐波注入电网，给电力系统带来了很大的危害，瞬时谐波参数估计能够为电力谐波治理提供科学依据。仿真结果表明，本文方法除了在谐波参数瞬变处存在较大的误差之外，其余各采样处瞬时振幅相对误差在2.0%左右，瞬时频率相对误差保持在0.5%左右，具有较高的估计精度，能实现瞬时谐波测量及分析。适用于电力系统的谐波补偿和谐波污染，及电力故障诊断和保护及电力负荷的识别等领域。

[1]刘劲磊（Liu Jinlei）.三相电路瞬时谐波检测算法（An algorithm of instantaneous harmonic detection in threephase circuit）[D].天津：天津大学电气与自动化工程学院（Tianjin：School of Electrical Engineering and Automation，Tianjin University），2007.

[2]曾博，滕召胜（Zeng Bo，Teng Zhaosheng）.纳托尔窗改进FFT动态谐波参数估计方法（Improved FFT approach for the dynamic state estimation of harmonic parameters based on the Nuttall window）[J].中国电机工程学报（Proceedings of the CSEE），2010，30（1）：65-71.

[3]Heydt G T，Fjeld P S，Liu C C，et al.Applications of the windowed FFT to electric power quality assessment[J].IEEE Trans on Power Delivery，1999，14（4）：1411-1416.

[4]蒋春芳，刘敏（Jiang Chunfang，Liu Min）.基于双插值FFT算法的间谐波分析（Inter-harmonics analysis based on double interpolation FFT algorithm）[J].电力系统保护与控制（Power System Protection and Control），2010，38（3）：11-14，19.

[5]Weruaga L，Kepesi M.The fan-chirp transform for nonstationary harmonic signals[J].Signal Processing，2007，87（6）：1504-1522.

[6]Hahn S.Hilbert Transforms in Signal Processing[M]. Boston：Artech House，1996.

[7]Bettayeb M，Qidwai U.Recursive estimation of power system harmonics[J].Electric Power System Research，1998，47（2）：143-152.

[8]魏晓璞，徐永海，郭春林，等（Wei Xiaopu，Xu Yonghai，Guo Chunlin，et al）.基于Hilbert变换与Pisarenko谐波分解的电压闪变参数估计（Parameter estimation of voltage flicker based on Hilbert transform and Pisarenko harmonic decomposition）[J].电力系统保护与控制（Power System Protection and Control），2010，38（6）：26-29，34.

[9]罗谌持，张明（Luo Chenchi，Zhang Ming）.基于Sigma点卡尔曼滤波器的电力频率跟踪新算法（Frequency tracking of distorted power signal using complex Sigma point Kalman filter）[J].电力系统自动化（Automation of Electric Power Systems），2008，32（13）：35-39.

[10]Maragos P，Kaiser J F，Quatieri T F.Energy separation in signal modulations with application to speech analysis[J]. IEEE Trans on Signal Processing，1993，41（10）：3024-3051.

[11]陈长升，黄险峰（Chen Changsheng，Huang Xianfeng）.基于小波变换抗混叠谐波检测的一种新方法（A novel method for anti-aliasing harmonic detection based on wavelet transform）[J].电力系统保护与控制（Power System Protection and Control），2008，36（23）：23-26，31.

[12]张鹏，李红斌（Zhang Peng，Li Hongbin）.一种基于离散小波变换的谐波分析方法（A novel algorithm for harmonic analysis based on discrete wavelet transforms）[J].电工技术学报（Transactions of China Electrotechnical Society），2012，27（3）：252-259.

[13]Barros J，Diego R I.Analysis of harmonics in power systems using the wavelet-packet transform[J].IEEE Trans on Instrumentation and Measurement，2008，57（1）：63-69.

[14]Terzija V V.Improved recursive Newton-type algorithm for power system relaying and measurement[J].IEEE Trans on Instrumentation and Measurement，1998，145（1）：877-881.

[15]乐叶青，徐政（Le Yeqing，Xu Zheng）.基于时频分布的电能质量交叉扰动检测（Crossed power quality disturbances detection based on the time-frequency distribution）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2007，19（6）：114-117.

[16]Petrovsky A，Azarov E，Petrovsky A.Hybrid signal decomposition based on instantaneous harmonic parameters and perceptually motivated wavelet packets for scalable audio coding[J].Signal Processing，2011，91（6）：1489-1504.

Novel Method for Instantaneous Harmonic Parameters Estimation

LÜ Gan-yun1，2，WU Chuan-man2，WU Yu-cong2，LI Jun1
（1.Department of Electrical Engineering，Nanjing Institute of Technology，Nanjing 210014，China；2.Department of Information Science and Engineering，Zhejiang Normal University，Jinhua 321004，China）

In order to tackle the instantaneous parameters estimation of dynamic harmonic，a novel method is proposed for instantaneous harmonic parameters estimation.It is assumed that each harmonic component of a signal is spaced in frequency-limited domain in this paper.The output signal of the band-pass filter can be obtained via the signal convolution with the impulse response of an ideal band-pass filter.By expanding each filter output at the zero frequency，instantaneous parameter of the corresponding harmonic component can be estimated，and the instantaneous harmonic parameters estimation of multi-component signals can be realized.The results indicate that the method can archieve instantaneous amplitude and frequency estimation for dynamic harmonic，and it has high performance of precision and real-time utilization.

band-pass filter；multi-component signal；instantaneous harmonic；parameter estimation；harmonic component

TM714

A

1003-8930（2014）09-0007-05

吕干云（1976—），男，博士，教授，研究方向为电能质量及人工智能在电力系统中的应用。Email：ganyun_lv@yahoo.co

2012-11-29；

2013-05-18

国家自然科学基金项目（51107120，51147010）；江苏省属高校自然科学基金项目（11KJB470007）；南京工程学院校级科研基金项目（YKJ201214）

吴传满（1986—），男，硕士研究生，研究方向为电能质量分析智能电表设计。Email：stmc17@sina.com

吴育聪（1987—），男，硕士研究生，研究方向为电能质量分析。Email：jacksaon@126.com