基于逆系统内模算法的双馈风力发电系统解耦控制

安友彬，李春茂，张祖杰，李坤

(西南交通大学 电气工程学院，四川 成都 610031)

基于逆系统内模算法的双馈风力发电系统解耦控制

安友彬，李春茂，张祖杰，李坤

(西南交通大学 电气工程学院，四川 成都 610031)

应用多变量非线性控制的逆系统方法，将双馈风力发电机这一多变量、非线性、强耦合系统精确解耦成有功和无功两个一阶线性子系统。对形成的伪线性系统，引入一种改进型内模控制结构，提高了控制系统的鲁棒稳定性和高阶无静差跟踪性能。仿真结果表明，提出的基于逆系统内模控制策略成功实现了有功、无功的解耦控制和最大风能追踪控制，系统具有更高的控制精度和稳定性。

双馈发电机；逆系统；双口内模结构；解耦控制

1 引言

随着传统能源短缺和环境污染日益加剧，以风能为代表的可再生能源的开发利用受到很多国家的重视。变速恒频双馈风力发电系统由于运行性能优越、优点突出，成为风力发电领域广泛应用的主流机型[1]。双馈风力发电系统的高性能控制也成为国内外研究的热点。目前，双馈风力发电系统的控制主要有交流电机变频调速的矢量控制策略、双通道多变量反馈控制策略等[2-3]。

它们大都在忽略了定子电阻情况下按照定子磁链矢量或电压矢量定向，认为定子电压与磁链矢量正交，结合电机模型推导出转子电流两个正交分量与输出有功和无功功率的关系，再在内环引入补偿电压消除转子电压方程中的交叉耦合项，最终实现转子电压对有功和无功的解耦控制。但是，由于双馈发电机动态过程转子反电势的存在，转子电压和转子电流的两个正交分量并不是完全解耦的关系[4]，因此通过静态电压补偿来实现有功和无功解耦控制具有局限性。故上述控制只能满足系统的稳态性能，而且由于上述控制策略在系统稳定点附近进行控制器设计，当系统运行参数变化或出现大的扰动时，系统闭环极点可能偏离稳定点而使解耦控制失败。

鉴于矢量控制存在的不足，从双馈风力发电系统非线性本质出发来进行完全解耦的控制设计，提高其静态和动态性能是很有必要的。本文通过引入基于逆系统的内模控制，实现了双馈风力发电系统的精确解耦控制，提高系统鲁棒稳定性和高阶无静差跟踪性能。

2 双馈发电机状态方程

定子侧和转子侧都采用电动机惯例，即定、转子电流都以流入电机方向为正。由电机学理论，两相同步旋转d-q坐标系下双馈发电机数学模型为[5]：

(1)

(2)

式中：Rs、Rr为定、转子绕组电阻；Ls、Lr、Lm为定、转子绕组自感与互感；usd、usq、urd、urq为定、转子电压；isd、isq、ird、irq为定、转子电流；ω1、ωs、ωr为发电机同步角速度、转差角速度和转子电角速度；J、np分别为转动惯量与极对数；p为微分算子；Te、Tm为电磁转矩和风力机输入转矩。

取系统状态变量为x=[isd,isq,ird,irq,ωr]T，输入控制量u=[u1,u2]T=[urd,urq]T，可得双馈发电机的状态方程为：

(3)

3 基于系统内模算法的双馈风力发电系统控制策略

3.1 双馈发电机的逆系统模型

图1 定子电压定向坐标系关系

交流励磁双馈发电机控制目标是控制定子发出的有功、无功功率，优化发电机功率因数，维持电网稳定。因此实现双馈风力发电系统输出功率的解耦控制是发电机运行的基本要求，也是进行最大风能追踪的前提。

两相同步旋转坐标系按照定子电压定向(如图1所示)，获得usd=0,usq=Us。此时双馈发电机定子输出功率方程为：

(4)

从上式可见对双馈发电机定子电流d、q轴分量isd、isq进行控制，就可实现对定子输出有功功率P1和无功功率Q1的控制。可知双馈风力发电系统的输出变量为y=[y1,y2]T=[P1，Q1]T=[-3Usx2/2,-3Usx1/2]T。

为了分析系统可逆性，根据Interactor算法[6]，计算输出y=[y1,y1]T对时间的导数，直到显含输入变量u=[u1,u2]T。

(5)

(6)

由式(5)～(6)，有

(7)

及

(8)

u=φ(x,v1,v2)

(9)

由式(5)和式(6)解得逆系统Πα解析表达式为

(10)

将式(10)所表示的逆系统Πα串接在原系统Σ之前组成α=[1,1]T阶伪线性系统(如图2所示)，伪线性系统的理想传递函数可表示为

(11)

图2 基于逆系统的双馈风力发电系统解耦线性化

3.2 基于逆系统的改进型内模控制

上文分析，将α阶逆系统串联在原系统之前就会形成一个伪线性系统。设伪线性系统的传递函数为P(s)，内部模型为M(s)(即式(11)所示α阶积分传函)。考虑到非线性建模误差的存在、运行时参数漂移以及其他因素，形成的伪线性系统并不是理想的线性系统，P(s)可看成由若干线性系统组成的模型集合。在频域中可以描述为[7]：

(12)

其中，Lm为误差的上界。

图3为双口结构的内模控制，P(s)为伪线性系统，M(s)为内部模型，C1(s)为内模控制器。相较于常规内模控制，双口结构的内模控制增加C2(s)控制器将系统参考输入r和实际输出y之差反馈到控制端。通过对第二个控制器适当设计，必定能在跟踪性能、干扰抑制方面取得优于常规内模控制的控制效果[8]。

图3 双口结构内模控制结构图

(1)双口结构内模控制鲁棒稳定性分析

引理1：对于单位负反馈控制系统，具有建模误差的控制对象传递函数为P(s)，其内部模型为M(s)，控制器传递函数为C(s)，则保证闭环系统稳定的充要条件为：

(13)

定理1：图3所示的双口结构内模控制的闭环稳定的充要条件为

(14)

证明：由图3可得双口结构内模控制系统的闭环传递函数为：

(15)

将其等效为单位负反馈控制系统，则等效开环传递函数为：

(16)

显然，双口结构内模的等效控制器为：

(17)

将式(17)代入式(13)，化简得到双口结构内模控制闭环系统稳定条件为：

(2)双口结构内模控制的高阶无静差跟踪性能

假设图3中控制器C1(s)、C2(s)和伪线性系统P(s)稳定，且满足式(14)闭环系统稳定条件。当取控制器C1(s)=f(s)·M-1(s)=f(s)(1/sαj)-1=f(s)sαj，滤波器f(s)取一型结构1/(λs+1)αj，C2(s)取一般PID控制器C2(s)=K(1+τi/s+τds)，把上面控制器结构连同P(s)=M(s)[1+H(s)]代入式(16)得到：

(18)

注意到上式分母中式[(λs+1)αj-1]为一型，可见系统为2+αj阶无差系统，至少可实现对斜坡信号的跟踪。总结发现，双口结构内模控制系统的无差性能取决于滤波器f(s)和控制器C2(s)的积分项个数以及伪线性系统内部模型的积分个数，并且积分作用是相加的关系。f(s)若为一型滤波器，控制器C2(s)取PID时有一个积分环节，内部模型为1/s(即αj为1)，则系统为三型无差系统，其他情况可以此类推。可见，双口结构内模控制的跟踪性能大大优于常规的内模控制。

3.3 基于逆系统的双口结构内模控制策略

对逆系统与原系统形成α=[1,1]T阶伪线性系统P(s)，运用上面的基于逆系统内模算法进行控制设计。内部模型取为M(s)=diag(1/s,1/s)，内模控制器为C1(s)=f(s)·M-1(s)，其中f(s)取一型滤波器结构，则有：

(19)

第二个控制器C2(s)都取K(1+τi/s)形式的PI控制器，由式(18)可知此处改进型内模控制系统为三型无差系统，具有对加速度参考信号的跟踪能力。综上，得基于逆系统改进型内模控制功率解耦控制框图(如图4所示)。

图4 基于逆系统改进型内模控制的功率控制方案控制原理框图

4 仿真研究

双馈发电机参数：额定功率15kW，定子额定电压380V，电网频率f=50Hz，极对数np=3，同步转速n1=1000r/min，定子绕组电阻Rs=0.379Ω，转子绕组电阻Rr=0.314Ω，定子自感Ls=0.0438H，转子自感Lr=0.0449H，定转子互感Lm=0.0427H，转动惯量J=0.39kg·m2。

风力机参数：空气密度ρ=1.25kg/m3，叶片半径Rw=4.3m，齿轮箱增速比N=7.846，最佳叶尖速比λopt=8.1，最大风能利用系数Cρmax=0.48。

仿真时，双馈发电机在700rpm空载转速下进行空载并网控制。在仿真1s时刻进行并网操作。无功给定情况：在2s给定500var，4s变为1000var。风速给定情况：1～3s内风速给定为5.668m/s，在该风速下使得叶尖速比最大的最佳转速为800rpm；3～5s内风速给定为6.377m/s，对应的最佳转速为900rpm；5～7s给定风速为7.794m/s，对应的最佳转速1100rpm。

图5为并网后最大风能追踪过程中输出有功功率跟踪参考有功的波形。从波形效果看出，输出有功功率实现对参考有功功率的高精度跟踪。

图5 定子输出有功功率Pi与参考有功功率的关系

图6为输出无功功率跟踪参考无功的波形。输出无功功率上升阶段有10%超调，但很快便稳定跟踪上无功参考值。

图6 定子输出有功功率Q1与参考有功功率的关系

图7为最大风能追踪过程风力机输入转矩Tm和电磁转矩Te波形。图8为此过程电机转速波形。给定风速改变时，随着电磁转矩与风力机输入转矩趋于平衡，电机转速平稳过渡到对应该风速的最佳转速上：即1～3s风速为5.668m/s时，电机平稳达到其最佳转速800rpm;3～5s风速为6.377m/s时，达到最佳转速900rpm；5～7s风速为7.794m/s时，达到其最佳转速1100rpm。

图9反映了最大风能追踪过程，电机在最佳功率曲线平稳移动，直到最佳功率与风力机输出功率相等，此时电机转速稳定运行在最佳转速上，同时获得最大风能利用系数Cpmax(如图10所示)。

图7 最大风能追踪过程风力机输入转矩Tm和

图8 最大风能追踪过程电机转速变化波形

图9 风力机实际输出功率Pm和最佳追踪功率Popt的关系

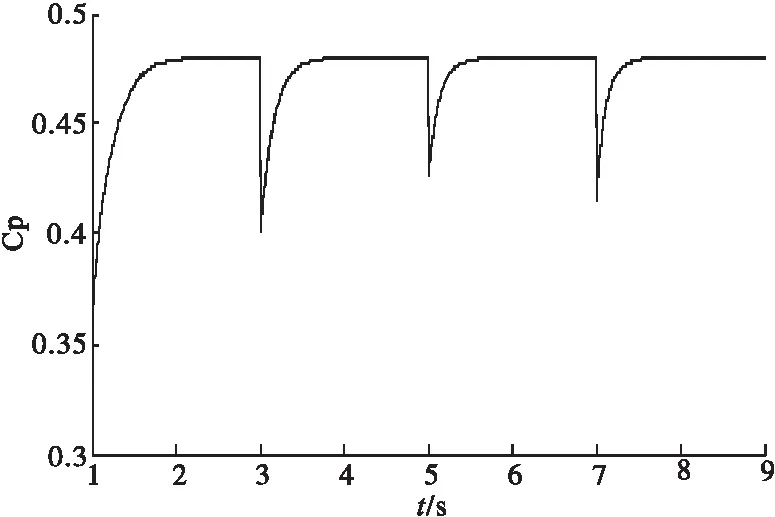
图10 风能利用系数波形

5 结语

本文在建立双馈发电机状态方程的基础上，采用非线性控制的逆系统方法，将双馈风力发电系统精确解耦成有功和无功两个一阶线性子系统。在此基础上采用一种改进型内模控制进行了综合设计。仿真结果表明，本文提出的基于逆系统内模控制很好地实现了有功、无功的精确解耦控制和最大风能追踪控制，并且控制系统具有很好的控制精度和动态性能。

[1] 任永峰，安中全.双馈式风力发电机组柔性并网运行与控制[M].北京：机械工业出版社，2011.7.

[2] 刘其辉，贺益康，张建华.交流磁链变速恒频风力发电系统的运行控制及建模仿真[J].中国电机工程学报，2006，26(5)：43-50.

[3] Guo Jia-hu.The Control Scheme Based on Inverse System Theory for Grid -connected Power Converter in Wind Turbine [C]//IC-MA2007，Harbin，China，Aug.5-8，2007:3690-3694.

[4] 郭家虎.变速恒频双馈风力发电系统控制技术的研究[D].上海：上海大学，2008.

[5] 陈伯时.电力拖动自动控制系统—运动控制系统[M].3版.北京：机械工业出版社，2003.

[6] 戴先中.多变量非线性系统的神经网络逆控制方法[M].北京：科学出版社，2005.

[7] 陈庆伟，吕朝霞，胡维礼，等.基于逆系统方法的非线性内模控制[J].自动化学报，2002，28(5)：715-721.

[8] George Stephanopoulos,Hsiao-Ping Huang.The 2-port control system [J] Chemical Engineering Science,1986,41(6):1611-1630.

Decoupling Control of Doubly-Fed Wind Power Generation System Basedon Inverse System Internal Model Algorithm

ANYou-bin，LIChun-mao，ZHANGZu-jie，LIKun

(School of Electrical Engineering,Southwest Jiaotong University,Chengdu 610031,China)

Applying the inverse system method of multivariable nonlinear control,the doubly-fed wind power generator precisely is decoupled into two first-order linear subsystems of active and reactive power which is a multivariable,nonlinear and strong coupling system.Introduce a modified internal model control structure to the pseudo linear system,to improve the robust stability and high order no static error tracking performance of the control system.Simulation results show that the proposed internal model control strategy based on inverse system,has successfully realized the decoupling control of active and reactive power and the maximum wind power tracking control,the system has higher control precision and stability.

doubly-fed wind power generator;inverse system;two-port internal model;decoupling control

李向新(1982- )，男，硕士研究生，主要研究电能质量和电力系统通信； 张颖(1962- )，男，教授，硕士生导师，主要研究电能质量及电力系统通信； 刘美容(1977- )，女，讲师，博士后,主要研究电路故障诊断及电力系统。

1004-289X(2014)02-0025-06

TM61

B

2013-06-08