灰色预测模型在蚌埠市公路客运量预测中的应用

徐建平，徐昙云，卢 杨

(1.江西省高速公路投资集团有限责任公司;2.江西省交通工程集团公司;3.长安大学)

0 引 言

公路客运量预测是对公路客运的发展趋势的动态分析，正确预测公路客运量对地区的经济发展格局和资源配置及公路运输企业的投资结构等都有重要作用。科学准确地预测公路客运量，不仅是公路客运专项规划的基础，也是制定综合交通规划等的前提。准确的把握客运发展趋势，对促进运输资源优化配置，发挥各种运输的最大效率，提高政府决策的科学性，对于加速建立现代化综合交通体系具有十分重要的参考价值。通过引入灰色系统理论，以蚌埠市为例，运用灰色预测理论对蚌埠市公路客运量进行预测，以把握蚌埠市公路客运的发展趋势，对优化公路客运资源配置、建立完善的公路客运市场具有十分重要的意义;同时，也可作为相关问题的决策及指标的制定提供科学、可靠的理论依据。

1 灰色预测模型在交通预测中的特点

灰色系统模型是中国学者邓聚龙教授于1982年创立的一种在少数据、信息缺乏的情况下对不确定性问题进行研究的新方法。由于交通运输量是一个受多层次、多因素影响的复杂关系量，为了准确的对它进行预测，需要考虑各个方面的影响因素，收集大量的信息，由此带来的问题是建模较困难，并且相应的计算工作量大;在一些情况下，即使能够建立出相应的模型但因缺乏足够的信息，相应的参数不能被确定，导致模型不能够实现预测。邓聚龙教授的灰色系统理论所提出的灰色模型预测方法，有效避开了这些复杂的相互关系，它主要着眼于系统存在的灰色信息，寻找出系统的内在规律，以达到使灰色系统明确化的目的。

2 GM(1，1)预测模型的建立及检验

2.1 GM(1，1) 预测模型建立

(1)累加生成

GM(1，1)是灰色预测模型中最常用的一种，本文采用该模型对蚌埠市公路客运量进行预测。已知原始数据序列，由它产生的r 次累加生成r－AGO，得出r－ AGO 的表达形式为，其中

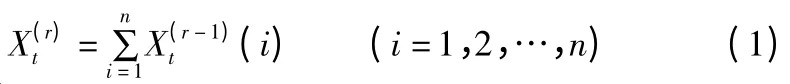
对X(0)进行一次累加生成，得到生成序列

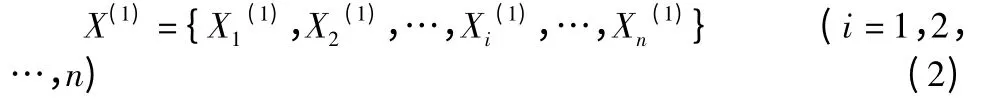
(2)建模

由X(1)构造背景值序列Z(0)={Z(1)(1)，Z(1)(2)，…，Z(1)(n)}，其中:

Z(1)(k)=aX(1)(k－1)+(1－a)X(1)(k) (k=2，3，4…n，一般取a=0.5)

得到GM(1，1)灰微分方程如下

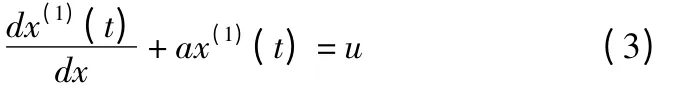
(3)求解参数

用最小二乘法，可以解得式(3)中的参数a，u。式中:a为发展系数，其大小反映了序列X(0)的增长速度;u 为灰作用量。令，有

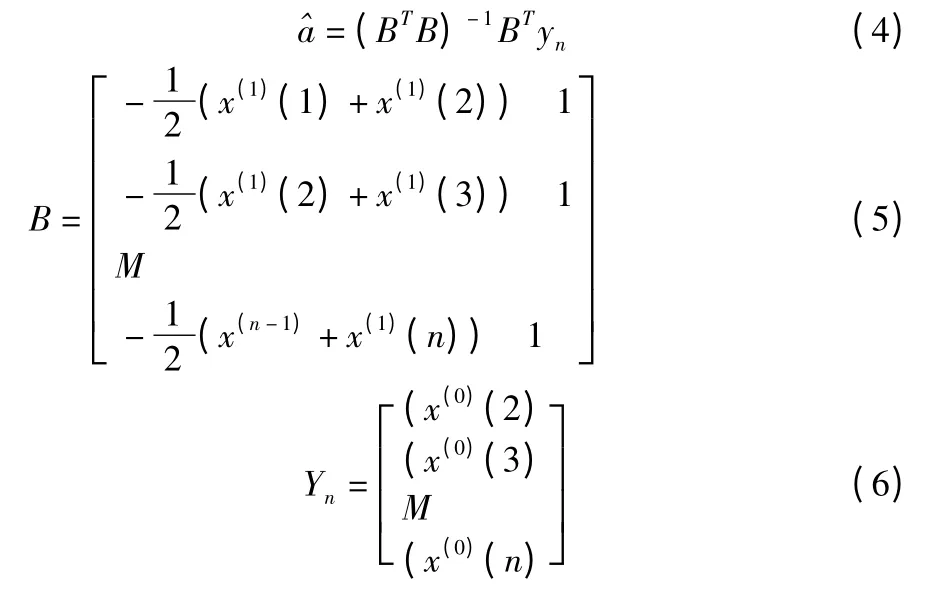
(4)建立预测公式

X(1)时间相应序列为

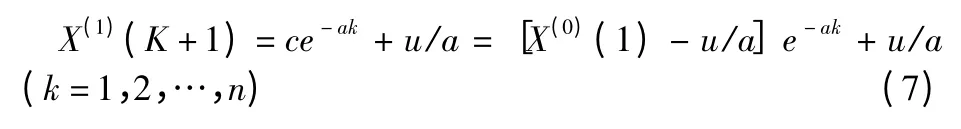
则离基年时间为k年的预测公式为:

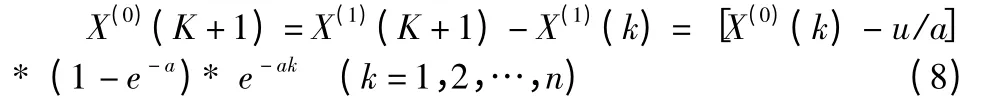
2.2 灰色系统模型的检验

灰色系统预测模型建立的科学与否，需要经过残差检验、关联度检验和后验差检验，只有通过这些检验才能运用模型进行预测。其中，模型精度检验标准如下表1 所示。

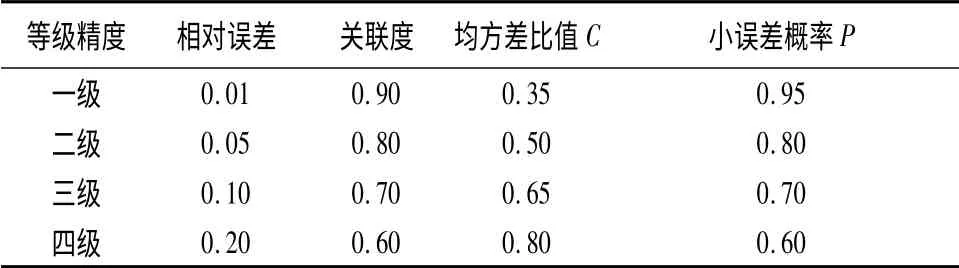
表1 模型精度检验标准

只有当模型依次通过了残差检验、关联度检验和后验差检验，则可用所建立模型进行预测。否则，需要进行残差修正。

3 灰色系统模型预测蚌埠市公路客运量

3.1 具体灰色系统模型的建立

以蚌埠公路客运行业数据为基础，应用公路客运量发展的灰色预测模型。根据上述的影响因素，选取蚌埠市2009～2011年公路客运量做相关性分析，各项统计值见表2 所示。

表2 蚌埠市2009 ～2011 数据统计表

近年来蚌埠市公路客运量增长迅猛，2009年至2011年三年之间增长44.8%，考虑到蚌埠市近年来经济的发展形势以及公路对经济的制约，蚌埠市在未来10年内会继续加大公路基础建设以满足公路客运需求的增长。在灰色系统模型中，以2009年为基年来进行预测，即X1(0)=9 326(万人次)。

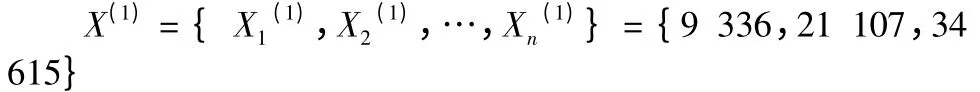
用最小二乘法，可以解得上式中的参数a，u。式中:a 为发展系数，其大小反映了序列X(0)的增长速度;u 为灰作用量。

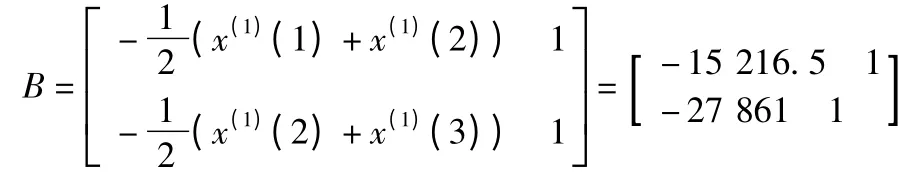
把以上数据代入公式可得

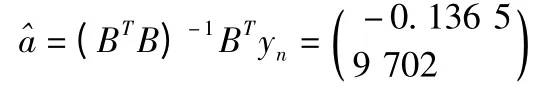
可知a=－0.136 5，u=9 702，将其代入式可得

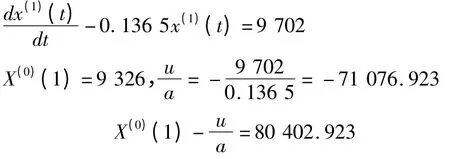
故有

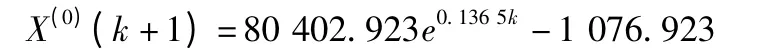
得出预测模型:

3.2 灰色系统模型的检验

模型不是一成不变的，一个模型只有经过残检验、关联度检验和后验差检验，判断其合理后才能进行预测。

(1)残差检验

按预测模型计算x(1)(i)，并将x(1)(i)累减生成x(0)(i)，然后计算原始序列x(0)(i)与x(0)(i)间的绝对误差序列和相对误差序列Φ(i):

将k=0，1，2 分别代入预测模型便得

X(1)={9 326，21 085，34 564.5}

累减生成序列X(0)序列

X(0)={9 326，11 759，13 479.5}

代入相应公式，得到绝对误差序列和相对误差序列

Δ(0)={0，22，28.5}

φ(i)={0，0.187%，0.211%}

(2)关联度检验

关联系数的计算

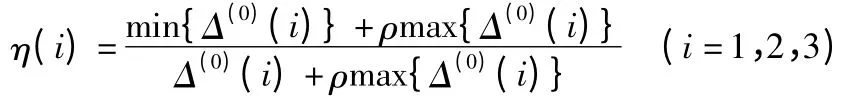
式中:ρ 为分辨率.0 ＜ρ ＜1，一般情况下，ρ=0.5。

将数据代入上式，得

η(i)={1，0.493 1，0.433 3}

关联度的计算

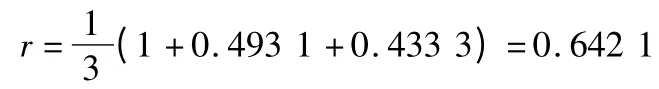
根据经验，当ρ=0.5 时，关联度r ＞0.6 即可。

(3)后验差检验

①计算原始序列标准差

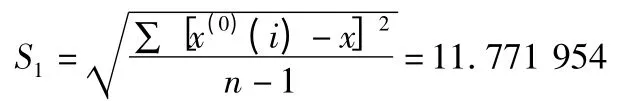
②计算绝对误差序列标准差

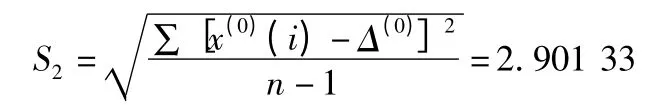
③计算方差比

④小误差概率

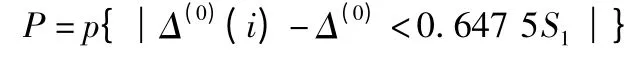
令S0=0.674 5S1，

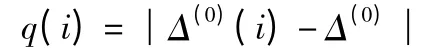
代入数据得S0=0.674 5，S1=11.987 2，q(i)={2.958，1.358，1.127}。

由于q(i)＜0.674 5S1，故P=1，c=0.163 74 ＜0.35。对照表1，可知预测模型合格。

模型通过了残差检验、关联度检验和后验差检验，故可用所建立模型进行预测。

3.3 蚌埠市公路客运量灰色模型预测值

最后确定的预测公式为:

X(0)(k+1)= X(1)(k +1)－ X(1)(k)=80 402.923*(e0.1365k－e0.1365(k－1))

故灰色预测模型预测的2020年的公路客运量为:

Y2020=X(1)(11 +1)－X(1)(10 +1)=40 171(万人次)

4 总 结

由于2011年的公路客运量为13 508 万人次，而2020年的公路客运量预测值为40 171 万人次，这说明蚌埠市的公路客运量将会快速增长，这必然会对蚌埠市的公路客运市场及公路基础施产生巨大的影响。

总体来看，将会导致蚌埠市的公路网存在一些问题:一是路网结构与交通高效转换的要求不相适应。高速、干线与农村公路网络都还不够完善，相互衔接不够顺畅，迂回路线偏少，转换效率不高，规模效益难以有效发挥;二是公路保畅应急能力与交通流加速增长的需求不相适应。特别是部分出口以及改扩建路段交通堵塞，呈现出发生频率高、持续时间长、疏导难度大、社会影响大的新特点，公路保畅、应急保障压力空前增大。

［1］邓聚龙.灰色控制系统［M］.武汉:华中理工大学出版社，1993.

［2］江志华，朱国宝.灰色预测模型GM(1，1)及其在交通运量预测中的应用［J］.武汉理工大学学报，2004，28(2).

［3］李思锋，郭天榜.灰色系统理论及其应用(第二版)［M］.北京:科学出版社，1999.

［4］张拥军，叶怀珍，任民.神经网络模型预测运输货运量［J］.西南交通大学学报，1999.34(5):602－605.

［5］张新天，罗晓辉.灰色理论与模型在交通预测中的应用［J］.公路，2001，8(8):4－7.