火灾下钢筋混凝土构件的可靠性设计

乔 牧， 盖芳芳， 赵继涛

(黑龙江科技大学 理学院，哈尔滨150022)

现代建筑向高层化发展，火灾对建筑物内部人员及建筑物本身的危害越来越大，因此，建筑防火问题成为学界研究的重点。建筑构件在高温的作用下，其材料的力学性能将严重退化，进而导致构件内力重新分布、构件承载力降低、结构变形增大，甚至造成结构破坏和倒塌。欧美国家先后成立了混凝土结构抗火研究组织，研究火灾反应和计算方法［1］。国内研究虽然起步较晚，但在结构抗火设计方法研究方面也取得了一些成果。现行的欧洲规范［2］采用确定性的力学模型来描述构件承载力的降低，这一方法虽然算法简单、思路清晰，却忽略了工程实践中的各种不确定性情况。传统方法强度折减系数的取值采用经验方法，根据实验构件在不同高温作用下各个时刻的失效概率来调整，对材料、计算方法以及荷载的不确定性情况无法给出科学的解释。将可靠性理论推广至建筑物及其构件的抗火性能研究领域，对于研究建筑物的耐火性能具有重要意义。基于此，笔者将构件的耐火极限设计与其可靠度有机结合，提出一种建筑物构件耐火极限设计方法。

1 设计方法

1．1 中心安全系数的确定

总体来说，结构设计的原则是，构件的抗力必须不小于荷载效应。按照可靠度设计方法，由于抗力与荷载的随机性，绝对安全的结构式是不存在的，只能认为结构在一定概率下可以满足设计要求。因此，高温作用下钢筋混凝土结构的可靠度设计要求为，在保证失效概率小于某一数值的条件下荷载不大于抗力。

传统的建筑设计方法是采用安全系数来增减荷载和抗力。此方法便于计算，但存在明显不足，将构件的强度和其所受到的应力看作确定量忽略了真实工况的种种不确定性，且无法得到不同条件下结构的失效概率。文中将可靠性算法引入安全系数法，既保持了传统方法的便捷，又科学解释了真实工况的变异性［2］。安全系数可以表示为抗力随机变量与荷载随机变量之比，即

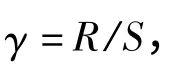
式中:γ——安全系数;

R——抗力随机变量;

S——荷载随机变量。

若假设构件强度与所受应力的概率密度函数分别为fR(R)和fS(S)，且强度和应力相互独立，则可得安全系数的概率密度函数［3］:

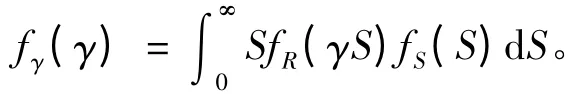
结构可靠度和失效概率可分别表示为:

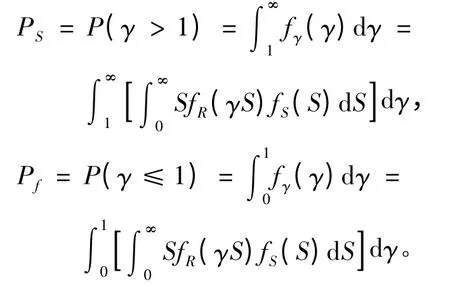
根据切比雪夫不等式可以得到

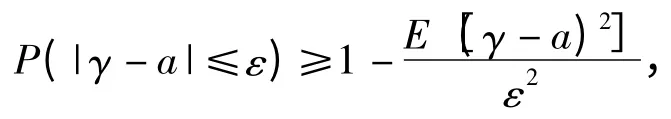
则

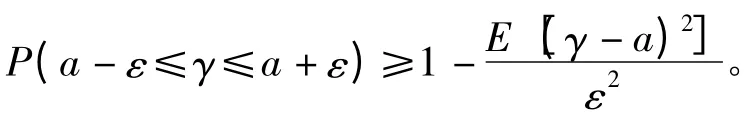
令a－ε=1，则

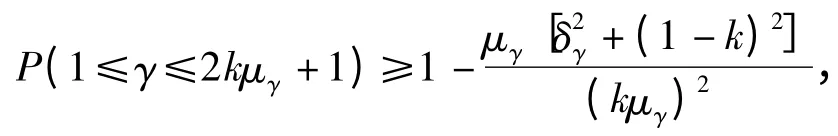
式中:μγ——随机变量γ 的均值;

δγ——随机变量γ 的变异系数;

k ——任意常数。

推导可得

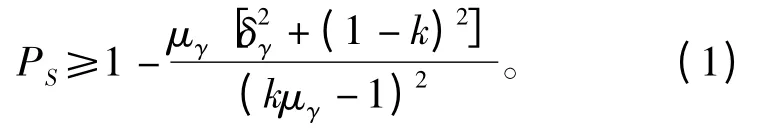
令

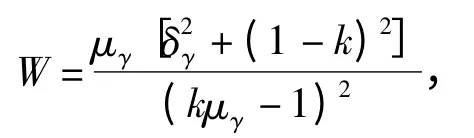
求解W 对k 的极小值可以求得极值点，代入式(1)可得:

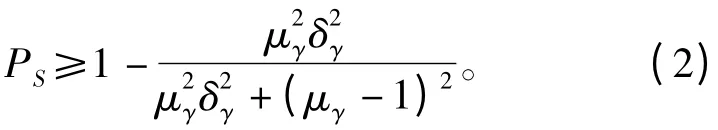
当目标可靠度确定后，安全系数γ 的均值可以通过式(2)求得，

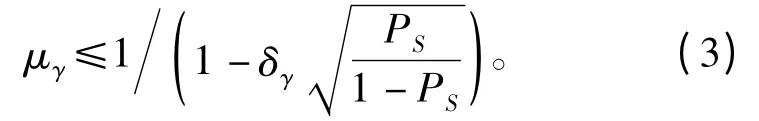
根据式(2)和式(3)，在μγ已知的情况下，安全系数的取值范围应为1≤γ≤(2k*μγ－1)，γ 的变异系数为

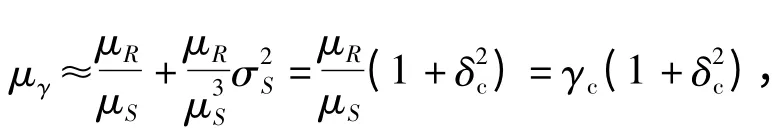
式中:γc——中心安全系数;

μR——抗力的均值;

μS——荷载的均值;

σS——荷载的标准差。

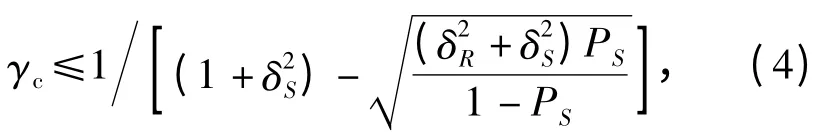
式中:δR——抗力的变异系数;

δS——荷载的变异系数。

当强度和应力的分布无法确定时，可以利用式(4)来估计安全系数的范围。假设应力和强度均服从正态分布，令可求得一次二阶矩法可靠性指标表达式为

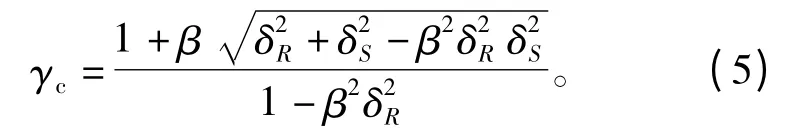
1.2 构件可靠性的设计

在求出了中心安全系数后，结构可靠性设计可表述为μR≥γcμS。假设功能函数中含有两个随机变量Xi和Xj，定义分离函数φi和φj分别为

则有

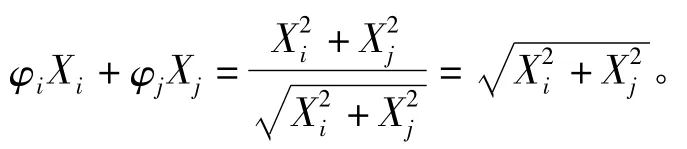
进而，当功能函数是由n 个互相独立的随机变量所确定，即Z =(x1，x2，…，xn)时，在均值点处将其台劳展开，即可推得Z 的均值和方差的近似值:

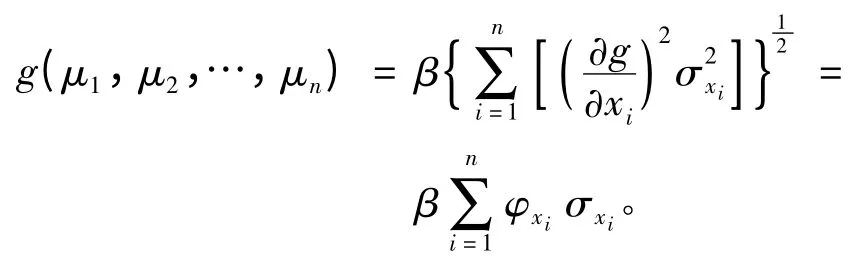
对于文中所涉及的钢筋混凝土结构的功能函数，Z=g(R，G，Q)=R －G －Q，当假设R、G、Q 均服从正态分布时可以采用上述方法计算。因此有

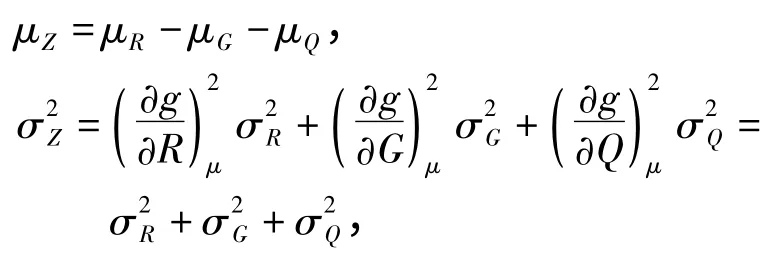
故

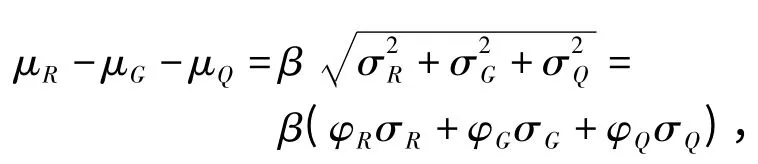
整理后可得

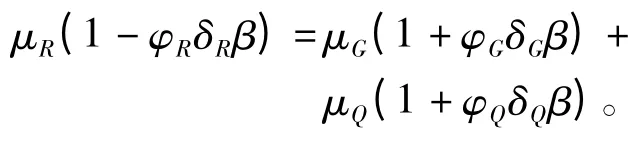
由此可得分项系数

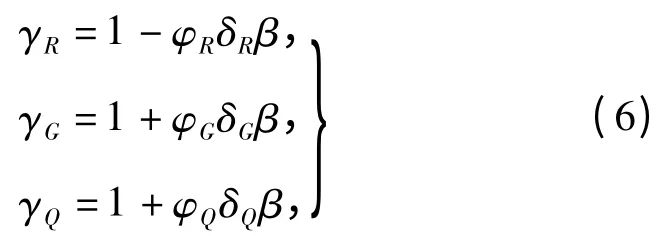
其中，

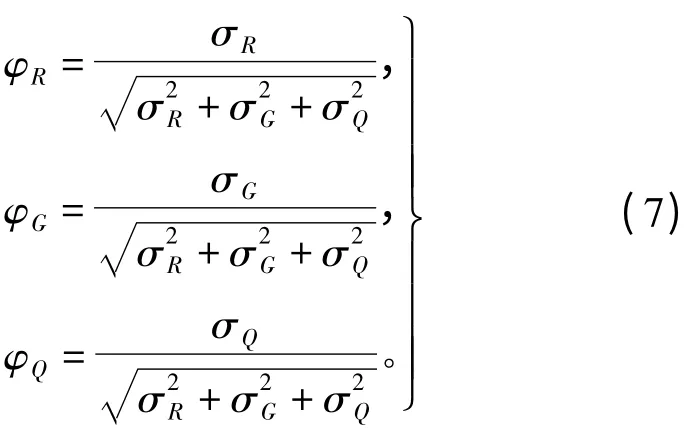
基于可靠性的安全系数定义，结构构件在高温的作用下其抗力的衰减过程决定了可靠性安全系数是一个随机过程，在任意时刻抗力取决于时间的函数φ(t)。由式(7)可知，假定恒荷载与活荷载G、Q为随机变量，其方差的取值完全取决于σR。为了计算方便，假定抗力和荷载均服从正态分布，计算表明该方法对精度影响不大。

在这里，求得的构件抗力不是某一时刻构件的瞬时抗力，而是在目标可靠度约束下构件抗力应该满足的条件。对于梁构件受高温作用的可靠性设计来说，抗力可表示为

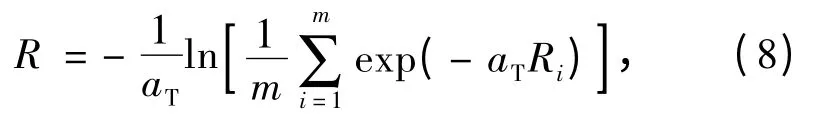
式中:Ri——加温过程中某一时刻构件抗力;

aT——活荷载取极大值时对应的分布函数参数。

通过升温曲线确定温度场的分布后，可以采用式(8)判断结构能否满足目标可靠度的要求。

2 算 例

某钢筋混凝土矩形截面简支梁，跨度为l =4.0 m，截面宽度b=300 mm，高度h=600 mm，配筋率取为0.9%，采用C30 混凝土，保护层厚度d =30 mm。假设其所受的荷载和抗力均服从正态分布，且μG=9.54 kN·m，σG=0.668 kN·m，μQ=36.078 kN·m，σQ=8.406 kN·m，采用ISO834 升温曲线，计算(1)若该梁在设计耐火极限内的可靠性指标满足规范要求，其抗力应满足的条件;(2)若已知构件的耐火极限和目标可靠度，求对常温下构件的承载力的要求。

解 (1)常温下梁的抗力可以按照混凝土规范方法求得，受弯钢筋用量

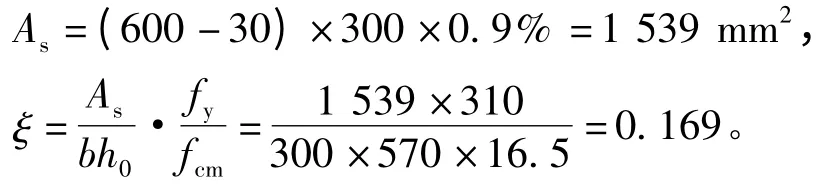
已知αs=0.154，因此初始状态极限抗弯承载力

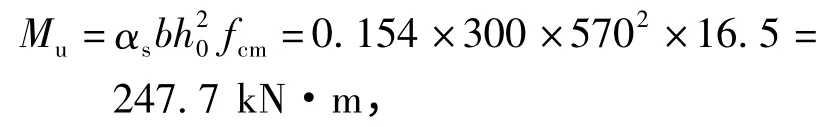
则由文献［4］可知，

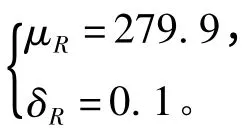
在ISO834 曲线作用下各时刻梁截面温度场如图1 所示。参照文献［2，5 －6］的计算方法，此梁加热60 min时的综合抗力计算式为

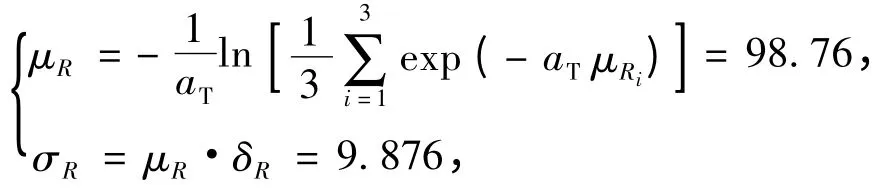
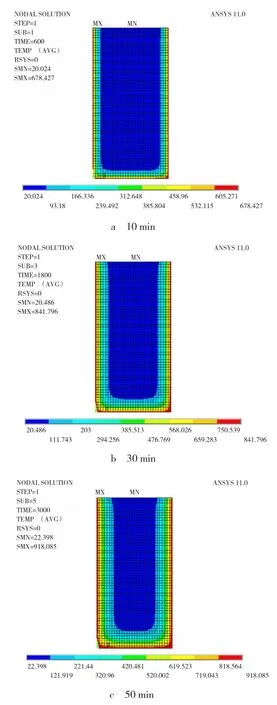
图1 梁在不同时间的温度场Fig．1 Beam temperature distribution

故有

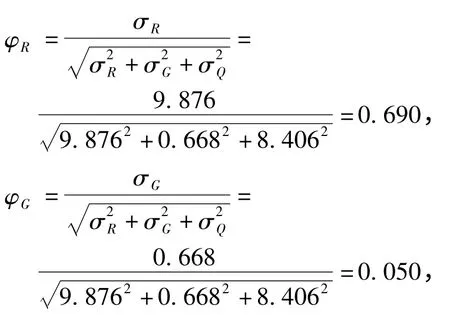
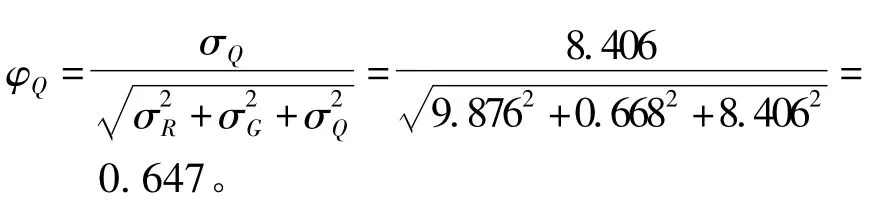
若所求钢筋混凝土梁要在受火作用60 min 后保证可靠性指标

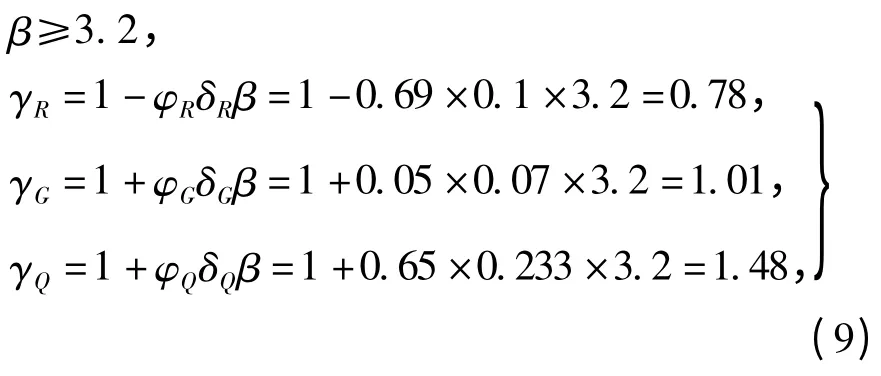
则有设计表达式

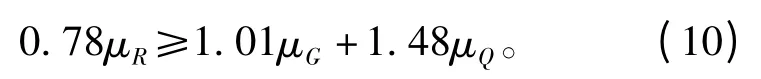
将抗力以及荷载代入式(9)可知，不等式成立，此梁能够达到规范要求的可靠度指标β≥3.2［6－7］，由文献［5］可知，此梁受火灾作用60 min 时可靠性指标为3.471 2，验证了文中结论的正确性。

(2)当耐火极限以及目标可靠度指标确定后，采用式(8)可以求出构件在常温下抗力应该满足的条件。不妨假设耐火极限为60 min，目标可靠度指标β=3.2，为了方便比较，假设混凝土构件的基本条件不变，其抗力服从对数正态分布，活荷载服从极值I型分布，且其对应的均值和方差不变，带入式(8)可得

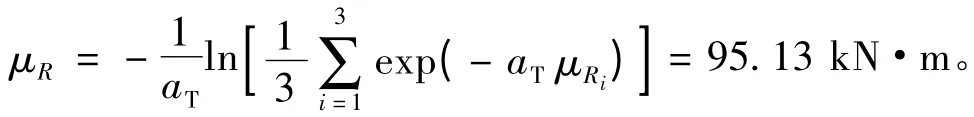
显然，上例中构件的抗力在常温下为279.9 kN·m ＞95.13 kN·m，能够满足设计要求。

3 结束语

笔者提出了一种基于可靠性安全系数法的钢筋混凝土结构抗火设计方法。根据高温下梁的承载能力与其常温下承载力的密切相关性，在梁的耐火极限与目标可靠度要求给定时，求其常温下所需的承载力，并以算例形式求解了钢筋混凝土梁在ISO834标准升温曲线作用下，其抗力与荷载应满足的条件方程。文献对比结果验证了算法的可行性。该方法能够科学解释结构及其所受荷载的变异性，同时又较为简单，易于掌握。

［1］TERRO MOHAMAD J．Numerical modeling of the behavior of concrete structures in fire［J］．ACI Structural Journal，1998，95(2):183 －193．

［2］侯晓萌，郑文忠．欧洲规范中混凝土结构抗火设计主要内容(1)——火灾下荷载效应、抗力效应、材料性能与基于表格的抗火设计方法［J］．工业建筑，2008，38(4):98 －103．

［3］何水清，王 善．结构可靠性分析与设计［M］．北京:国防工业出版社，1993:37 －65．

［4］乔 牧．火灾下建筑结构构件时变可靠性分析［D］．哈尔滨:哈尔滨工程大学，2011:31 －33．

［5］乔 牧，王振清，朱大雷，等．高温下钢筋混凝土梁的时变可靠性分析［J］．哈尔滨工程大学学报，2011，32(8):997－1000．

［6］WANG ZHENQING，QIAO MU，ZHU DALEI，et al．The reliability analysis of reinforced concrete beams under high temperature［C］//2010 Third International Joint Conference on Computational Science and Optimization(CSO2010)．Huangshan:［s．n．］，2010:327 －330．

［7］中华人民共和国住房和城乡建设部．GB50010—2002 混凝土结构设计规范［S］．北京:中国建筑工业出版社，2011．