90°弯管内流体流动数值模拟研究

王金娥 杨小江

（1.武汉船舶职业技术学院 动力工程学院，湖北武汉 430050；2.杭州市港航管理局，浙江杭州 310014）

弯管广泛应用于水利、化工、石油、动力工程等领域，弯管中的流动由于受到弯管曲率的影响，相比直管的流场要复杂的多，而且会在管壁附近形成分离区、管道截面上产生二次流动等，这不仅会造成流体总压和能量的损失，而且形成的局部障碍区域也使流动系统的阻力增大，会降低热量和质量交换的效率［1］。疏浚作业在航道整治、港口建设、湖泊清淤和吹填造地等工程中应用广泛并发挥着重大作用。在疏浚施工过程中，疏浚泥浆经过长距离输泥管道从挖掘水域排放至泥浆存放点，疏浚泥浆具有成份复杂、浓度高和颗粒不均的特点，因此阻力大、能耗高、堵塞管道和排泥距离受限等问题在长距离输送的过程中普遍存在，并严重影响着疏浚挖泥船的生产效率、作业范围和生产成本。本文以直径为50mm的输送管道为研究对象，以多相流理论为依据，通过理论分析、弯管内流场CFD模拟来输泥管道的阻力特性。

1 控制方程及计算模型

1.1 控制方程

设流体空间点的平均流速和平均压强分别用和表示，在直角坐标系中，雷诺平均RANS方程可用下式表示［2］：

式中：αk——k方程的湍流Prandtl数；

αε——ε方程的湍流Prandtl数；

Gk——由平均速度梯度引起的湍动能生成项；

在ε方程中，Rε为ε方程中的附加源项目，代表平均应变率对ε的影响，Rε的表达式为：

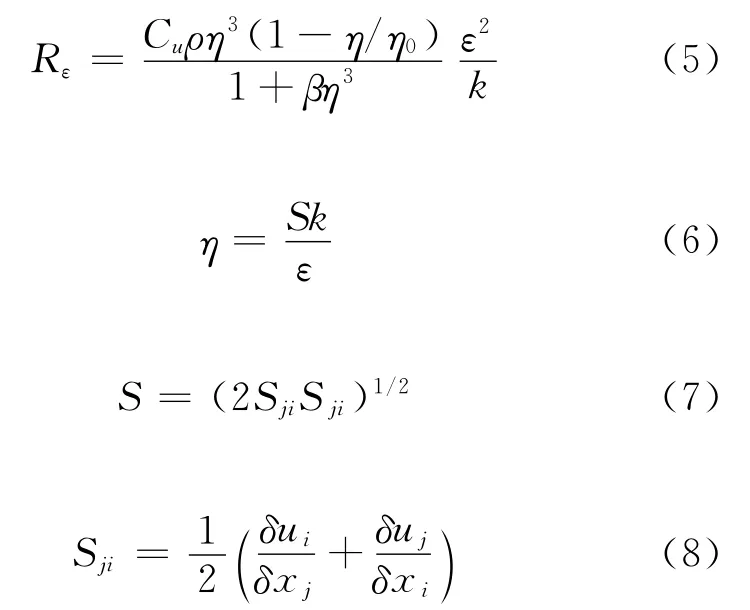
上述方程的模型参数为：η0＝4.38；β＝0.012；Cu＝0.0845；C1ε＝1.42；C2ε＝1.68；αk＝αε＝0.7194；。其中η是无量纲应变，或者湍流时间与应变尺度的比值，代表平均应变率ε对的影响［3］。

RNGК－ε湍流模型既适应高雷诺数情况，也适应低雷诺数下的湍流流动，即提供了一个微分形式的有效粘性系数表达式，以说明低雷诺数流动效应。此外，对于湍流Prandtl数，RNGК－ε湍流模式提供了一个解析式，而标准湍流模式使用了经验常数［4］。

1.2 物理模型

本文以90°圆截面弯管为研究对象，将弯管分为三个部分：上游水平直线段、弯曲段和下游竖直直线段。弯管管直径为50mm，如图1所示。

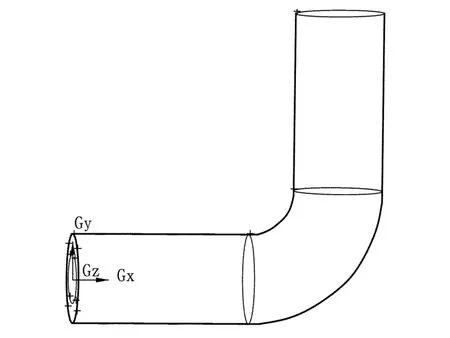
图1 90°弯管模型图

1.3 网格划分

在划分网格过程中，遵循由线到面，由面到体的划分原则。对弯管进口表面的网格选用了四边形类型，边长设为1.25mm；对直管段进行体网格划分时采用用四边形向对应的六面体网格来进行划分，壁面网格边长设为2mm；而对于弯管端，由于此处流态变化复杂需要捕捉更为准确的流场信息，所以对此处网格进行加密处理，壁面网格边长设为1mm。如下图2所示。

图2 入口端面（左）－直管段（中）－弯管段（右）网格图

在本文中，最终修正后的模型节点数有128616个，网格单元有122341个。整体网格划分图如图3所示。

图3 90°弯管网格划分图

2 数值模拟

2.1 边界条件的设定

设置弯管左侧的平面为速度入口边界inlet，类型设为VELOCITY－INLET；右侧的出口面为出口边界outlet，类型设为OUTFLOW，壁面类型为 WALL（默认）。最后输出网格File→Export→ Mesh，并保存文件，为FLUENT进行仿真计算做好准备。

2.2 结果输出及分析

因为有非线性的对流项存在，在N－S方程的原参数形式求解过程中，一定要使用迭代求解，收敛性的问题必然会遇到。其中一个重要的关系到精度和经济的问题就是收敛标准，如收敛标准过高，CPU的运算时间过长，会直接导致死循环和发散；但是收敛标准也不能过低，否则不收敛的结果会被输出。

取流速v为2m／s，方向垂直于进口截面，分别选取水和浓度的泥浆作为流动介质，入口压力p＝4.5KPa（相对于大气压），管内温度t＝293K，管径d＝0.05m。水的密度ρ1＝998.2kg／m3，动力粘度μ1＝0.001Pa·s；泥浆的密度ρ2＝1225kg／m3，动力粘度μ2＝0.02Pa·s。

雷诺数Re、湍流强度I的计算公式如下：

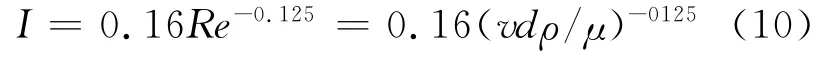
通过上式计算出流动介质为水时雷诺数Re1＝9.982×104，远大于临界雷诺数2300，所以管内为湍流流动，湍流强度I1＝0.038。

流动介质为30%浓度泥浆时雷诺数Re1＝6.125×103，也大于临界雷诺数，所以管内为湍流流动，湍流强I2＝0.054度。

定义进口边界条件并且初始化流场：水流速度v＝2m／s，湍流强度I＝0.038，水力直径d＝0.05m，从进口边界inlet进行初始化计算，经过59次迭代计算，残差达到收敛标准。泥浆流速v＝2m／s，湍流强度I0.054，水力直径d＝0.05m，从进口边界inlet进行初始化计算，经过66次迭代计算，残差达到收敛标准。

图4 清水－泥浆计算收敛对比图

2.3 压力分布及结果分析

流动介质为水和泥浆时的压力分布如下图5所示。

从图5可以看出，流体在弯管的内弯和外弯处发生明显变化，在经过外弯拐点时压强达到最大值，而当流体经过内弯拐点的时候达到最小值，并在弯管段的内测产生负压，因此在该处容易发生气蚀现象。液体在出口管的压力是从弯管的内侧到外侧逐渐增大，在管道轴线附近达到和进口管处相近的压力。由于泥浆粘度比清水粘度要大，经过弯管段的压力损失也要比介质为清水时的压力损失大，所以介质为泥浆时的出口压力比介质为清水时的出口压力小。

图5 水（左）－泥浆（右）的压力分布云图

2.4 速度分布及结果分析

流动介质分别为清水和泥浆时弯管速度分布如图6所示。

从图6可以看出，流体在弯管段的速度分布和压力分布是相反的，在弯道的内测处速度达到最大值3.1m／s，但是在弯道外侧处达到最小值，速度几乎为零。所以该处有较大的速度变化，容易产生管壁磨损。当流体流过弯管段之后进入直管段时，流体在管道内测明显形成一个低流速区域，靠近管壁处流速接近于零，由内到外逐渐增大，并在管道轴线附近达到接近进口处的流速2m／s。

通过对比，泥浆流过弯管段到直管段后的靠近管壁内测的低流速区域要明显比介质为清水时的低流速区域要大，说明泥浆经过弯管时的流动速度的扰动要比清水时大。

图6 水（左）－泥浆（右）速度分布对比图

3 结 语

本文运用fluent对90°弯管内流场进行了模拟并进行了深入分析，可以得出以下结论：

（1）运用RNGК－ε湍流模型模拟包括有旋均匀剪切流、自由流、边界层流以及有分离的流动等在内的各种湍流流动具有较好的效果；

（2）压强方面，由于流体在运动过程中受到弯管曲率的影响，离心作用逐渐由内侧被甩到曲率半径较大的外侧壁面附近，众多流体推挤外侧壁面，另外在流体输运工程中的能量的损失，弯管内侧和外侧的压力分布明显不同，沿轴向的压力梯度很大，且呈现出靠近内侧壁面区域的压力值小，外侧壁面附近区域压力值较大。

（3）流速方面，由于流体的输送压力以及弯管曲率的不同等各方面的因素，弯管外壁面附近的流体速度较小，而内壁面附近的流体的速度相对较大。

1 丁 珏，翁培奋.90°弯管内流动的理论模型及流动特性的数值研究［J］.计算力学学报，2004，21（3）：314－321.

2 李进良，李承曦，胡仁喜.精通FLUENT 6.3流场分析［M］.北京：化学工业出版社，2009：82－99.

3 朱红钧，林元华，谢龙汉.Fluent 12流体分析及工程仿真［M］.北京：清华大学出版社，2011：37－41.

4 周俊波，刘洋.FLUENT 6.3流场分析从入门到精通［M］.北京：机械工业出版社，2012：164－170.