活动轮廓模型影像分割方法综述

李妍

(武汉大学测绘学院，武汉 430079)

1 引 言

影像分割在影像处理和计算机视觉领域有着重要的应用。最近20年左右一些新的影像分割方法不断涌现，其中活动轮廓模型方法在近10年来得到了广泛的关注。活动轮廓模型源于Kass等提出的Snake模型[1]。早期的活动轮廓模型演化曲线由于采用显式参数表达(因而称为参数活动轮廓模型)导致其无法解决区域的拓扑变化问题，因而限制了该方法的使用。后来Osher和Sethian提出了水平集的方法[2]，将演化曲线(面)用隐式水平集的方式进行表达，称为几何活动轮廓模型，或者水平集方法。引入水平集函数的最大优点是能够自然地处理曲线(面)的拓扑变化，因而可以检测多个物体的边缘。因此水平集方法从很大程度上推动了活动轮廓模型影像分割方法的发展，使得该方法成为图像分割领域的一大新的分支。目前用到的活动轮廓模型方法都基本都属于几何活动轮廓模型，由于其在轮廓的表达中引入了水平集函数，在具体能量泛函最小化的解算中用到了变分理论，因而也被称为变分水平集方法。

几何活动轮廓模型进行影像分割的基本思想是利用水平集理论和影像的边缘(梯度)或者区域的灰度信息构造能量泛函并给定一个初始轮廓，然后利用变分理论对偏微分方程进行迭代计算实现初始轮廓的变形演化，最终达到能量泛函最小化，此时对应的轮廓曲线即是分割的目标边界。图1概况了活动轮廓模型的一些基本分类情况。

本文主要从能量泛函的表达和解算、分割区域的数目、能量泛函的构造、能量泛函数据项中包含的基本信息和其他信息等方面对活动轮廓模型进行总结和概括，并重点介绍一些经典的能量泛函模型，同时涵盖了活动轮廓模型的一些最新研究进展。

图1 影像分割的活动轮廓模型方法基本分类图

2 能量泛函包含的基本信息

几何活动轮廓模型中最常用的基本信息有梯度信息和区域的灰度信息。利用梯度信息时称为边缘活动轮廓模型，而利用区域的整体灰度信息时称为区域活动轮廓模型。

2.1 边缘活动轮廓模型

边缘活动轮廓模型有多种，此处仅以应用范围最广的Snake模型和测地线活动轮廓模型为代表进行简单介绍。

2.1.1 Snake模型[1]

Snake模型是最早的活动轮廓模型，其基本思想在感兴趣区域附近给出一条初始轮廓曲线(可变形曲线)，然后使得曲线在能量泛函逐渐递减的引导下在图像中发生变形并不断逼近目标轮廓。模型中的变形曲线用参量表示为C(s)=(x(s),y(s)),s∈[0,1]，其能量泛函为：

(1)

其中C′和C″分别代表变形曲线对参数s的一阶和二阶偏导。式(1)的梯度下降流为：

(2)

作为最早的活动轮廓模型，Snake模型存在许多不足，如分割结果对曲线的初始位置和形状较敏感；通常不能改变轮廓线的拓扑结构以分割多个目标或具有复杂拓扑结构的目标；外力场的作用范围小；很难将颜色、纹理或者运动信息等其他信息纳入模型等。

2.1.2 测地线活动轮廓模型[3]

测地线活动轮廓模型利用了光学中的Fermat原理，即光在不均匀介质中传播时，“光线”将不是沿直线，而是按最短光程的方式确定其路径。利用这一原理，可用如下能量泛函的最小化来确定活动轮廓：

(3)

式中L(C)表示闭合曲线C的弧长，g为边缘指示函数，作用是使轮廓曲线到达目标边界时停止演化，其定义如下：

(4)

最小化式(3)所对应的梯度下降方程为：

(5)

基于边缘的活动轮廓模型主要是利用目标的边缘信息来进行影像分割，进而提取目标边界。当影像没有明显的边缘或者边缘较弱，同时又缺乏明显的纹理特征时，这一类型的影像分割方法就很难得到理想的效果。因此在该方法发展的同时也出现了另一个研究方向——基于区域的活动轮廓模型。

2.2 区域活动轮廓模型

早期的基于区域的活动轮廓模型以Mumford-Shah模型[4]为代表，但该模型只是一个理论框架，实际求解非常困难。后来Chan和Vese将该模型简化，并利用水平集函数提出了无边缘活动轮廓模型[5](简称Chan-Vese模型)，其能量泛函可以表示为：

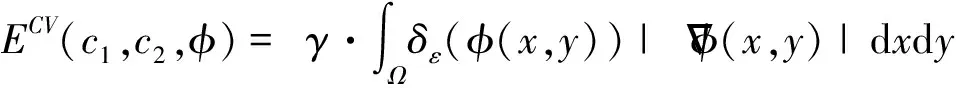
(6)

其中Hε(φ)和δε(φ)分别阶跃函数H(φ)和狄拉克函数δ(φ)的C∞规则近似项：

(7)

在实际数值计算时通常取ε=1。式(6)对应的梯度下降方程为：

(8)

由于Chan-Vese模型简单且易实现，因而后来的许多研究都是在该模型的基础上进行改进的。

基于区域的几何活动轮廓模型使用图像的区域特征作为分割条件，因此对弱边缘的分割效果优于基于边缘的方法，而且能够同时实现影像的去噪和分割。但是该方法忽略了对图像的细节和局部边缘信息，因此分割效果受到一定的影响。对此，通常有两种解决方案：①在能量模型中引入局部信息(见本文第四部分的论述)；②是将影像的边缘特征、区域特征以及统计特征等各种特征集于一体，从而构建分割效果更佳的混合模型。所以，之后又出现了混合型活动轮廓模型。

2.3 混合型活动轮廓模型

混合型活动轮廓模型[6-7]集成了影像的局部边缘信息和区域的综合信息，因而可以更加有效地实现影像的分割。Bresson等[8]提出了一种联合边界、区域和形状信息的变分模型，并且利用几何形状先验知识以及全局和局部影像信息，得到了很好的分割结果。然而，该模型的先验知识由PCA模型获得，需要大量的训练样本。Allili和Ziou[9]提出了一种联合边缘和区域极化信息的分割模型，该模型可以分割纹理信息非常强的影像。Zhang等[10]利用测地线模型和Chan-Vese模型，提出了一种SBGFRLS(Selective Binary and Gaussian Filtering Regularized Level Set) 模型。该模型可以有效提取照度均匀的影像，但对于照度不均匀的影像分割效果不佳。Tian等[11]提出了一种包含边缘项、区域项和规则项的混合模型，该模型能够分割普通场景(包括亮度不均匀影像)。

3 多相影像分割

上述给出的模型主要是针对影像中只有目标和背景两类地物的简单场景，因而只适用于两相影像分割。在很多情况下，由于影像中的场景比较复杂，背景和目标之间的分离不能简单地用两相分割来处理，因此必须要将两相影像分割模型拓展到多相影像分割。活动轮廓模型中多相影像分割方法大致可以分为以下3种类型：

①类似于二叉树的形式，采取自上而下的策略，先进行整幅影像的两相分割，再对子区域进行两相分割，如此迭代往复直到影像全部分割完毕[12]；

②对一个水平集函数分层以达到多相分割的目的[13]；

③用多个水平集函数进行多相分割[14-15]。

由于篇幅所限，这里仅对应用和研究较多的第3种类型稍加叙述。根据分割区域数目和采用水平集函数数目的不同，可以得到如表1所示的不同多相分割方案。由于多相影像分割中，每次迭代计算时均需要将所有水平集函数进行更新，因而迭代计算量会随着水平集函数数目的增加而大大增加，因此从计算效率的角度讲，方案2的计算效率最高。令χi(x)为区域Ωi的特征函数，n为分割的区域数目。这里给出方案2对应的能量泛函公式：

嘉宾席里却少了掌声相应。刚才梅宏图的开场白，把大家搞得一头雾水，面面相觑。新闻界的同行们？啥意思？一个搞房地产的问题商人，不会连“同行”是什么意思也搞不清楚吧？他奶奶的个小脚，这年头，咋净是专家出自文盲富翁起于草莽的怪现象层出不穷呢？

(9)

表1 多区域分割方案表(单位：个)

无论采用哪种分割方案，能量函数中的特征函数χi必须满足以下两个条件才能避免重叠或者漏分问题：

而且通常与两相影像分割类似，均可以利用梯度下降方程进行迭代计算，从而实现初始轮廓随时间的演化，最终实现影像的多相分割。

4 能量泛函中包含的其他信息

在Chan-Vese模型中主要用到了区域的灰度均值信息，对于含有一定噪声的影像或者纹理影像该模型分割效果不佳，因而研究人员又在此基础上提出了一系列的改进方法，即将灰度分布的统计信息、纹理信息等影像特征纳入能量泛函的数据项中，以改善变分水平集影像分割效果。

4.1 灰度分布统计信息

将统计信息融入几何活动轮廓模型中使得影像分割的应用可以扩展到纹理影像和运动序列影像的分割。Zhu和Yuille[7]给出了MS模型及其贝叶斯最大后验概率MAP估计之间的联系的证明，而Paragios和Deriche[6]则给出了应用MAP模型进行最优化分割的计算方法。

假定影像分为两区域，各区域满足高斯统计分布，令

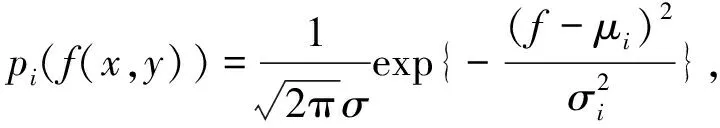
(10)

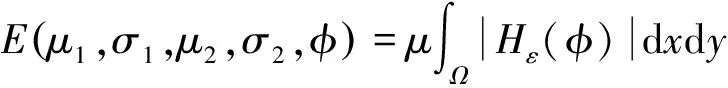
(11)

其对应的梯度下降方程为：

(12)

此外，Michailovich等[17]，Mitiche和Ayed[18]均研究了基于影像区域数据分布差异最大化进行影像两区域分割的数学模型。

4.2 纹理信息

对于纹理信息比较丰富的影像，将纹理描述子引入几何活动轮廓的能量泛函模型中将大大提高影像分割的效果。在水平集纹理影像分割中利用得比较多的纹理描述子有LBP(Local Binary Patterns)纹理[19-20]、Gabor纹理[21-22]、结构张量[23-24]等。

综上所述，除了影像亮度信息之外，影像的很多特征都可以引入变分水平集能量泛函中来代替像元本身的灰度信息，从而使得活动轮廓模型用于影像分割时具有非常好的可扩展性。这些特征可以是一个标量(如影像亮度)、一个矢量(如像元颜色或者时空影像梯度)，或者一个张量(例如结构张量或者扩散张量)等。

4.3 局部信息

当影像存在弱边缘或者影像上照度不均时，通常活动轮廓模型的分割效果会受到影响，最终导致分割错误。针对这一问题，研究人员提出了各种改进能量函数的方法，将影像的局部信息与全局信息结合起来，从而能够更好地分割弱边缘或者照度不均导致的模糊边界。例如将局部信息引入Chan-Vese模型的能量泛函中以提高演化曲线对弱边界的捕获能力[25-26]。此外，Salah等[27]将核函数引入能量泛函的数据项中；Bernard等[28]用B样条基函数的线性组合来表达零水平集，用该方法进行曲线演化时速度非常快。

5 全局凸分割模型及其求解

前面介绍的能量泛函都是非凸函数，因而在具体解算过程中存在两个根本性的问题：①能量泛函非凸使得分割结果易受初始轮廓的影响而陷入局部极值；②能量泛函均采用梯度下降方法求解，迭代次数多、计算量大，导致分割时间长，分割效率低下。虽然人们提出了窄带法和快速步进算法[29]从一定程度上改善了第2个问题，但能量泛函非凸的问题依然存在。

近些年来研究人员对经典Chan-Vese模型进行了各种改进[30-31]。其中较成功的是Chan等提出的全局凸分割GCS(Global Convex Segmentation，GCS)模型[30]，其相应的能量泛函为：

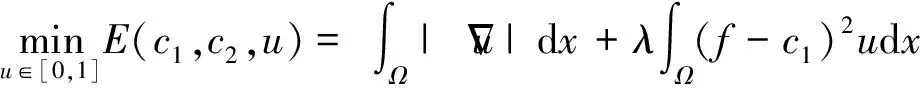
(13)

Goldstein等提出用Split Bregman算法对GCS模型进行快速求解[32-33]。其基本思想是引入矢量变量d以及Bregman迭代因子b，从而将能量泛函最小化问题分解为两个变量u和d的最优化问题：

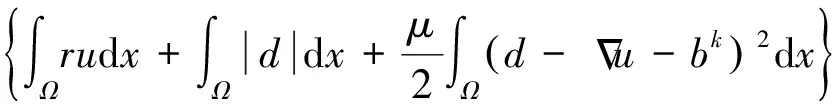
(14)

(15)

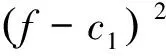
首先固定d，则式(14)所对应的最优化问题对于u的欧拉-拉格朗日方程为

(16)

对式(16)，可以用中心差分计算其中的拉普拉斯算子，用向后差分计算散度算子，从而得到式(16)的数值解方案为：

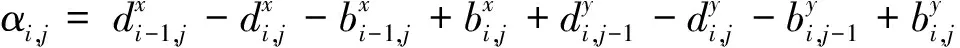
ui,j=max{min{βi,j,1},0}

(17)

然后固定水平集函数u，可以利用收缩算子求式(14)相对于d的最小值从而得到d的迭代计算式：

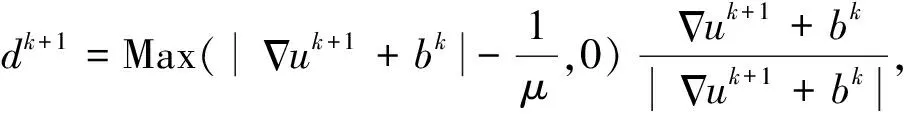
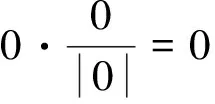
(18)

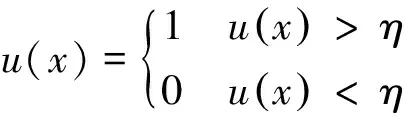
全局凸分割模型的出现较好地解决了经典Chan-Vese模型的非凸问题，Split Bregman快速算法则大大减少了全局凸分割模型的迭代次数和计算时间。但该模型只适用于两相影像分割，对于多相影像分割尚需进一步的研究。

6 结束语

利用影像的各种特征，将局部亮度扩展到局部特征，使得变分水平集的框架可以扩展到纹理影像分割、运动目标分割等，从而大大开拓了变分水平集影像分割的应用领域。从最初的简单影像分割到医学影像分割[34-36]，到目前的雷达影像等遥感影像分割[37-39]、动态影像目标跟踪[40-42]等，基于活动轮廓模型的影像分割方法的应用领域正在不断扩大。

参考文献：

[1] KASS M，WITKIN A，TERZOPOULOS D.Snakes：Active contour models[J].International Journal of Computer Vision，1988，1(4)：321-331.

[2] OSHER S，SETHIAN J A.Fronts propagating with curvature-dependent speed：Algorithms based on Hamilton-Jacobi formulations[J].Journal of Computational Physics，1988，79(1)：12-49.

[3] CASELLES V，KIMMEL R，SAPIRO G.Geodesic active contours[J].International Journal of Computer Vision，1997，22(1)：61-79.

[4] MUMFORD D，SHAH J.Optimal approximations by piecewise smooth functions and associated variational problems[J].Communications on Pure and Applied Mathematics，1989，42(5)：577-685.

[5] CHAN T F，VESE L A.Active contours without edges[J].IEEE Transactions on Image Processing，2001，10(2)：266-277.

[6] PARAGIOS N，DERICHE R.Geodesic active regions and level set methods for supervised texture segmentation[J].International Journal of Computer Vision，2002，46(3)：223-247.

[7] ZHU S C，YUILLE A.Region competition：Unifying snakes，region growing，and Bayes/MDL for multiband image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1996，18(9)：884-900.

[8] BRESSON X，VANDERGHEYNST P，THIRAN J-P.A variational model for object segmentation using boundary information and shape prior driven by the Mumford-Shah functional[J].International Journal of Computer Vision，2006，68(2)：145-162.

[9] ALLILI M S，ZIOU D.Globally adaptive region information for automatic color-texture image segmentation[J].Pattern Recognition Letters，2007，28(15)：1946-1956.

[10] ZHANG K，ZHANG L，SONG H，et al.Active contours with selective local or global segmentation：A new formulation and level set method[J].Image and Vision Computing，2010，28(4)：668-676.

[11] TIAN Y，DUAN F，ZHOU M，et al.Active contour model combining region and edge information[J].Machine Vision and Applications，2013，24(1)：47-61.

[12] CHUNG G，VESE L A.Energy minimization based segmentation and denoising using a multilayer level set approach[C].Energy Minimization Methodsin Computer Vision and Pattern Recognition，Lecture Notes in Computer Science，2005(3757)：439-455.

[13] GAO S，BUI T D.Image segmentation and selective smoothing by using Mumford-Shah model[J].IEEE Transactions on Image Processing，2005，14(10)：1537-1549.

[14] VESE L A，CHAN T.A multiphase level set framework for image segmentation using the Mumford and Shah model[J].International Journal of Computer Vision，2002，50(3)：271-293.

[15] HONG-KAI Z，CHAN T，MERRIMAN B，et al.A variational level set approach to multiphase motion[J].Journal of Computational Physics，1996，127(12)，179-195.

[16] ROUSSON M，DERICHE R.A variational framework for active and adaptative segmentation of vector valued images[C].Proceedings of IEEE Worksho Pon Motion and Video Computing，2002：56-61.

[17] MICHAILOVICH O，RATHI Y，TANNENBAUM A.Image segmentation using active contours driven by the Bhattacharyya gradient flow[J].IEEE Transactions on Image Processing，2007，16(11)：2787-2801.

[18] MITICHE A，AYED I B.Variational and level set methods in image segmentation[M].Springerverlag Berlin Heidelberg，2011.

[19] QING X，JIE Y，SIYI D.Texture segmentation using LBP embedded region competition[J].Electronic Letters on Computer Vision and Image Analysis，2005，5(1)：41-47.

[20] SAVELONAS M，IAKOVIDIS D，MAROULIS D.An LBP-based active contour algorithm for unsupervised texture segmentation[C].IEEE 18th International Conference on Pattern Recognition，2006(2)：279-282.

[21] SANDBERG B，CHAN T，VESE L.A level-set and gabor-based active contour algorithm for segmenting textured images[R].UCLA Department of Mathematics CAM Report，2002.

[22] 张立和，朱莉莉，米晓莉.结合Gabor纹理特征的局域化多通道水平集分割方法[J].电子学报，2011，20(7)：1569-1574.

[23] ROUSSON M，BROX T，DERICHE R.Active unsupervised texture segmentation on a diffusion based feature space[C].Proceedings of.IEEE Computer Society Conferenceon Computer Vision and Pattern Recognition，2003(2)：699-704.

[24] 王晓峰.水平集方法及其在图像分割中的应用研究[D].中国科学技术大学，2009.

[25] LANKTON S，TANNENBAUM A.Localizing region-based active contours[J].IEEE Transactions on Image Processing，2008，17(11)：2029-2039.

[26] LIU S，PENG Y.A local region-based Chan-Vese model for image segmentation[J].Pattern Recognition，2012，45(7)：2769-2779.

[27] BEN SALAH M，MITICHE A，BEN AYED I.Effective level set image segmentation with a kernel induced data term[J].IEEE Transactions on Image Processing，2010，19(1)：220-232.

[28] BERNARD O，FRIBOULET D，THEVENAEP，et al.Variational B-spline level-set：A linear filtering approach for fast deformable model evolution[J].IEEE Transactions on Image Processing，2009，18(6)：1179-1191.

[29] SETHIAN J A.Level set methods and fast marching methods：Evolving interfaces in computational geometry，fluid mechanics，computer vision，and materials science[M].Cambridge University Press，1999.

[30] CHAN T F，ESEDOGLU S，NIKOLOVA M.Algorithms for finding global minimizers of image segmentation and denoising models[J].SIAM Journal on Applied Mathematics，2006，66(5)：1632-1648.

[31] BRESSON X，ESEDOGLU S，VANDERGHEYNST P，et al.Fast global minimization of the active contour/snake model[J].Journal of Mathematical Imaging and Vision，2007，28(2)：151-167.

[32] GOLDSTEIN T，OSHER S.The split bregman method for l1-regularized problems[J].SIAM Journal on Imaging Sciences，2009，2(2)：323-343.

[33] GOLDSTEIN T，BRESSON X，OSHER S.Geometric applications of the split Bregman method：Segmentation and surface reconstruction[J].Journal of Scientific Computing，2010，45(1-3)：272-293.

[34] 董建园，郝重阳，齐敏.基于策略演化水平集的医学图像快速分割[J].中国图象图形学报.2009，14(8)：1689-1695.

[35] 高燕华，刘玉欢，喻罡.多尺度非参数化水平集的超声心动图分割[J].西安交通大学学报，47(2)：1-7.

[36] WANG L，LI C，SUN Q，et al.Active contours driven by local and global intensity fitting energy with application to brain MR image segmentation[J].Computerized Medical Imaging and Graphics，2009，33(7)，520-531.

[37] AYED I B，MITICHE A，BELHADJ Z.Multiregion level-set partitioning of synthetic aperture radar images[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27(5)：793-800.

[38] 贺志国.基于活动轮廓模型的SAR图像分割算法研究[D].国防科技大学，2008：22-41.

[39] 杨耘，马洪超，林颖，等.多水平集演化的高分辨率遥感影像分割[J].武汉大学学报(信息科学版)，2008，33(6)：588-591.

[40] MANSOURI A-R，KONRAD J.Multiple motion segmentation with level sets[J].IEEE Transactions on Image Processing，2003：12(2)，201-220.

[41] CREMERS D，SOATTO S.Motion competition：A variational approach to piecewise parametric motion segmentation[J].International Journal of Computer Vision，2005，62(3)：249-265.

[42] 于慧敏，徐艺，刘继忠，等.基于水平集的多运动目标时空分割与跟踪[J].中国图象图形学报，2007，12(7)：1218-1223.