非规则正射影像镶嵌多边形网络自动生成

项琳，岳贵杰，杜黎明

(1.中国测绘科学研究院,北京 100039;2.首都师范大学资源环境与旅游学院,北京 100048; 3.河南城建学院测绘工程学院,平顶山 467036)

1 引 言

在正射影像镶嵌处理中待镶嵌影像的有效范围一般为矩形区域。此类影像镶嵌网络的生成相对简单。通常采取手工或自动的方法提取重叠区域分割线，然后根据一定的规则生成整体的多边形网络[1]；当正射影像的有效像素区域为非四边形区域的，如何不对影像进行化简情况下自动生成镶嵌多边形网络显得十分重要。常用的数字摄影测量系统或遥感影像处理软件一般都采用人工方法进行两两影像镶嵌处理，在海量数据处理时，劳动强度大。

本文提出了一种非规则边缘正射影像的镶嵌多边形网络自动生成方法，将正射影像镶嵌多边形网络的生成细化为影像有效区域的提取、两两重叠区域的确定、重叠区域分割线的生成、初始镶嵌多边形网络的生成及多边形网络的拓扑编辑等过程。该流程能全自动生成唯一的、且具有良好几何特性的镶嵌多边形网络，减少了人工处理的工作量，提高了正射影像镶嵌的效率。

2 常用定义

影像有效范围：用多边形表示的影像有效像素范围。如图1中的红色多边形内部像素，无效像素为背景色(黑)，白色矩形边框为影像覆盖范围。

镶嵌多边形：在多幅影像的镶嵌过程中，需要确定每幅影像对镶嵌结果有贡献的像素多边形范围，称之为镶嵌多边形[1]。镶嵌多边形包含于影像有效范围内，如图2中的两个多边形分别包含在图1中的两个多边形内。

镶嵌多边形网络：在镶嵌区域中，由每幅影像的有效镶嵌多边形组成的多边形集合。在该多边形集合中，两两多边形没有交集。如图2中的两个多边形，图7的三个多边形。

拓扑孔洞：镶嵌多边形网络中存在的未被覆盖的部分。如图8中的点4、7、8和9组成的多边形(红色部分)。

跨接边：在多边形的三角剖分结果中，位于多边形内部的三角形的边称为跨接边。如图4中的虚线边。

边界边：镶嵌多边形组成的网络中仅出现一次的边，称为边界边。如图2中除去AB之间公共边之外的其他边。

非边界边：在多边形网络中出现两次，即相邻多边形之间的重合边(公共边)。如图2中的AB之间的公共边，图8中的点1和2,、点2和3，点3和4组成的边等。

3 镶嵌多边形网络生成步骤

本文中两幅影像镶嵌多边形网络自动生成流程为：①提取每一幅影像的有效像素范围，用多边形表示(图1中的两个红色多边形)；②求取两幅影像的重叠区域(图1中两个多边形的交集)；③计算重叠区域分割线(如图1中AB两点间的绿色线条)。分割线的起点和终点是两幅影像有效区域多边形的公共点(A点和B点)。若有多于两个公共点时，分割线可以有多条，此时需要采用优化算法得到满足条件的最优的一条分割线；④用求得的分割线分割两幅影像，得到镶嵌多边形，如图2中的两个红色多边形。

多幅影像镶嵌多边形网络的生成步骤类似于两两间的处理方法。对多幅影像处理时，将每一次分割后的结果作为下一次分割的输入，直至处理完与一幅影像有关的所有分割线。分割后的多边形构成初始镶嵌多边形网络，在该网络中，可能存在拓扑错误(孔洞)，需要进行孔洞检测及消除。

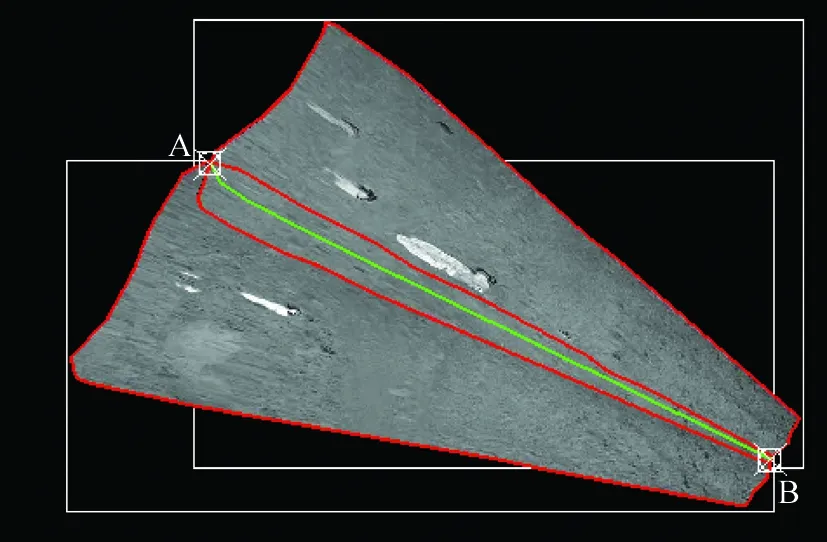
图1 两幅重叠影像及其分割线

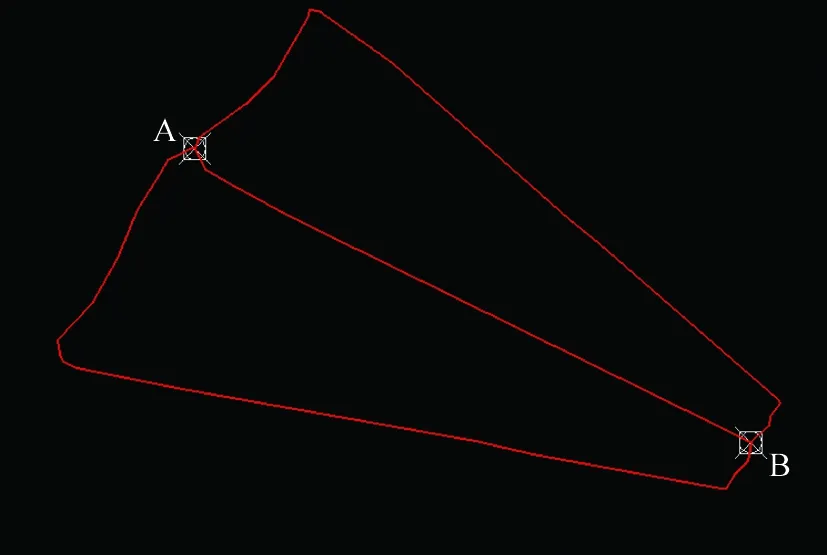
图2 分割线分割影像多边形

3.1 影像多边形的自动提取

自动镶嵌过程中，处理的是每一幅影像的有效像素，需要提取每一幅影像的有效像素范围，并用多边形表示。有效像素范围提取实质为轮廓跟踪问题，即通过顺序找出边缘点跟踪边界。轮廓跟踪常用的算法是基于4连通或8连通区域的方法。本文采用基于8连通区域的跟踪算法，其主要步骤：

① 按从上到下，从左到右扫描图像,寻找第一个边界点。

② 按一定准则逆时针搜索当前3×3邻域像素。

③ 直到得到闭合边界，则跟踪结束。

得到跟踪结果后，对多边形边界数据采用Douglas-Peucker矢量数据压缩方法进行压缩。由于Douglas-Peucker矢量数据压缩是针对曲线(首尾不相连)的压缩方法，对多边形处理时需要将多边形分解为两条曲线。分解时，选择多边形中距离最远的两个点将多边形分为两个曲线段。跟踪的结果如图1所示的两个红色多边形。

3.2 两两影像重叠区域的计算

跟踪所有影像的有效区域多边形后，需要确定所有多边形之间的重叠关系，即计算具有重叠关系的两两多边形之间的交集，本质为多边形的剪裁(求交集)问题。

本文采用Weiler多边形裁剪算法进行确定[2-3]交集多边形。该方法中首先确定主多边形和裁剪多边形，然后根据边的相交关系确定“出点”(主多边形由此离开裁剪多边形区域)和“入点”(主多边形由此进入裁剪多边形)，并把“出点”和“入点”坐标插入到多边形顶点表中，最后从多边形的顶点中按照顺时针或逆时针的顺序确定多边形的交集。

设多边形(顺时针)P1-P2-P3-P4为主多边形，多边形C1-C2-C3-C4-C5-C6为剪裁多边形。J1、J2、J3、J4、J5、J6、J7和J8为被剪裁多边形和剪裁多边形的交点，则图中的“入点”为J1、J3、J5和J7；“出点”为J2、J4、J6和J8。

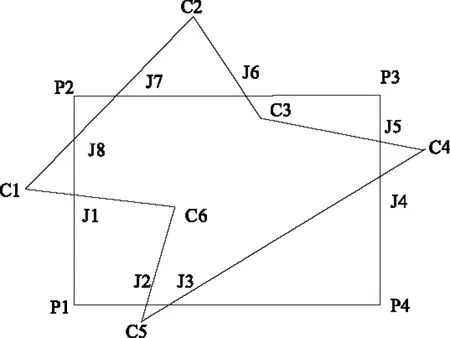
图3 Weiler多边形交集计算原理

交集查找方法(顺时针)：

① 从主多边形的起点开始搜索“入点”，如果该点未被查找过(未被标记)，则该“入点”作为交集多边形的起始点，并沿主多边形按顺时针进行顶点的搜集、查找。

② 碰到“出点”，则转入剪裁多边形进行搜索；

③ 直到被剪裁多边形中的所有“入点”均被查找；

该方法得到的两个多边形的交集J1-J8-J7-J6-C3-J5-J4-J3-J2-C6。

3.3 重叠区域分割线的生成

重叠区域分割线应尽量平分重叠区域。文中采用一种基于四叉树结构原理的多边形中任意两点间路径的提取算法进行分割线的提取，该算法的主要步骤：

① 首先对重叠区域多边形采用割耳(Ear Clipping)的方法进行三角剖分；

多边形的耳，是多边形中凸点与两个相邻点组成的三角形，而且对角线不与其他边相交。 Ear Clipping方法的主要原理为：逐次从多边形中割去一个耳作为剖分的结果，直至剩余最后一个三角形。

② 得到重叠区域多边形中的公共点(A点和B点)。

③ 采用四叉树遍历方法从剖分结果中提取指定起点和终点的分割线；

如图4表示多边形A～S的Ear Clipping三角形剖分结果(虚线)。假设B点和H点为指定的起点和终点(两个多边形的重叠区域中表示公共点)，采用四叉树结构遍历B点和H点之间路径的方法为：查找B点所在三角形的所有跨接边的中点(0,1,2)，分别以0,1,2为节点(共有三棵四叉树)遍历所有的跨接边的中点，直到查找到终点H所在三角形中的跨接边。若以点1为节点遍历，得到的路径图及四叉树表示如图4和图5所示：

图4 重叠多边形两点间路径

图5 两点间路径四叉树结构表示

指定起点和终点间的路径也可能有多条，需采取一定的优化方法提取最优的一条，如路径距离最短或分割多边形为两部分的面积差最小。

3.4 初始镶嵌网络的生成

初始镶嵌网络的生成方法流程如图6,图7和图8。图6中A、B和C为三张正射影像有效区域，ab、ac及bc分别为AB、AC、和BC两两间重叠区域的分割线，则镶嵌多边形生成步骤如下：

① 得到多边形相关的所有分割线,如图6中A多边形相关的分割线为ab,ac。

② 用每一条分割线分割多边形，并把分割后的多边形作为下一条分割线分割时的输入多边形，直到处理完所有的多边形和分割线。用图6中的ab和ac分别分割A多边形得到A1多边形(图7)，生成的初始多边形网络如图8所示。

图6 影像多边形及分割线

图7 初始镶嵌多边形

图8 初始镶嵌多边形网络

3.5 初始镶嵌多边形网络拓扑编辑

生成的初始镶嵌多边形可能含有孔洞(图 8)，在镶嵌过程中视之为拓扑错误。

(1) 镶嵌多边形网络中孔洞产生原理

在图6、图7和图8镶嵌多边形网络生成过程中，用ab、ac和bc分割三个多边形A、B和C时，由于三条分割线不相交于同一个点，分割时将可能产生孔洞。

(2) 孔洞的检测与消除

由上述定义6、7可知，在图8由A1，B1和C1组成的多边形网络中，点1、2边、点2、3边和点3、4边组成A1多边形和B1多边形的公共边。点5、6和7三边组成A1多边形和C1多边形的公共边，点9、10、11、12四边组成B1多边形和C1多边形的公共边。孔洞多边形(点4、7、8和9组成)的边出现一次，为边界边。由孔洞多边形产生原理又知，孔洞多边形的边是分割线的一部分。

基于孔洞多边形边的特点(属于边界边，并且为分割线上的一段)。本文提出了初始镶嵌多边形网络中，孔洞的自动检测方法：首先对镶嵌多边形边进行分类，并提取位于分割线之上的边界边(限制条件)，然后对得到的所有边界边进行首尾组合，生成封闭的多边形，即孔洞。

得到镶嵌多边形网络中孔洞后，可以采用多种方法消除孔洞。如以简单多边形内的任意一点代替孔洞多边形的各个顶点坐标，并用该点对镶嵌多边形网络中相应顶点进行更新替换，得到经过拓扑编辑的最终镶嵌线多边形网络。

4 镶嵌多边形网络生成与镶嵌结果

为测试本文所提方法的有效性，分别利用两个航带的航空影像数据(图9)和美国火星车影像数据(图12)进行正射影像镶嵌试验。图9中数据为两个航带共12幅影像,图12中数据为美国火星车影像制作得到的正射影像,共10幅。

图9、图12红色多边形为采用8-邻域方法跟踪得到的正射影像有效多边形范围，绿线为所有重叠区域的分割线。图10为得到的山区影像镶嵌多边形网络。图13为得到的火星影像初始镶嵌多边形网络，图13,图14为两个区域的镶嵌结果。

图9 山区影像多边形范围(红线)及分割线(绿线)

图10 山区影像镶嵌多边形网络

图11 山区影像镶嵌结果图

图12 火星车影像多边形范围(红)及分割线(绿)

图13 火星车影像镶嵌多边形网络

图14 火星车影像镶嵌结果图

5 结束语

正射影像镶嵌是摄影测量与遥感中数据生产的一项重要工作。本文采用自动化处理的流程替代手工镶嵌处理，可以方便，快捷地进行镶嵌处理，大大减轻了人工的工作量，且文中所述的镶嵌方法同样适用于规则边缘正射影像镶嵌处理，具有较好的应用价值。

参考文献：

[1] 潘俊,王密,李德仁.基于顾及重叠的面Voronoi图的接缝线网络生成方法[J].武汉大学学报(信息科学版),2009,34(5):518-521.

[2] WEILER K.Polygon comparison using a graph representation[J].Computer Graphics,1980(14):10-18.

[3] WEILER K, ATHERTON P. Hidden surface removal using polygon area sorting[J].Computer Graphics,1977,1(11):214-222.

[4] 马小虎,潘志庚,石教英.基于凹凸顶点判定的简单多边形Delaunay三角剖分[J].计算机辅助设计与图形学学报,1999,(1):1-6.

[5] 周培德.计算几何[M].北京:清华大学出版社,2001:212-235.

[6] 王中辉,闫浩文.多边形主骨架线提取算法的设计与实现[J].地理与地理信息科学,2011,27(1):43-48.

[7] 高福顺,高占恒,梁学章.三角网络中的孔洞修补算法[J].研究快报,2009,46(6).

[8] 邓敏,李志林,李光强.简单面目标与孔洞面目标间拓扑关系的层次表达方法[J].测绘学报.2008,37(3):330-337.

[9] 周晓光,陈军,蒋捷等.地籍地块间的空间拓扑关系[J].测绘学报,2003,32(4):356-361.

[10] 李根,陈志杨,张三元，等.网格曲面中复杂孔洞的自动修补算法[J].浙江大学学报(工学版),2007,41(3):407-411.