有效预应力空间分布确定方法

雷 宇

(上海市政工程设计研究总院(集团)有限公司，上海 200092)

预应力混凝土大型箱梁结构的整体抗裂性是一个相当复杂的问题，开裂是普遍现象。从受力上分析箱梁开裂的原因，发现常规设计的不足，明确常规设计的可靠性，对设计方法的改进具有重要意义。目前国内设计规范对箱梁桥设计主要是采用全截面的平截面假定，利用基于平面杆系的有限元方法求解，并通过一个内力增大系数计入箱梁横截面扭转翘曲、剪力滞、畸变的效应。这种方法对于箱梁尤其是跨径较大的箱梁结构是不合适的。因此，为了确保设计的安全性、合理性和耐久性，有必要对预应力混凝土连续刚构桥的空间受力特性和配筋方法进行分析，为桥梁抗裂性设计提供依据［1］。

1 预应力施加的模拟方法

预应力施加的模拟方法通常为初应变法和降温法，都是通过在力筋模型中产生拉应变来等效力筋被张拉时所产生的拉应变。初应变法是通过定义材料的初始属性来实现所需的拉应变，降温法是通过施加温度荷载来实现所需的拉应变。弹性分析时二者本质相同，非线性分析时存在差异。初应变法一般不考虑预应力损失，否则每个单元的实常数各不相等，建模工作量较大;降温法根据有效预应力的分布对各力筋单元施加相应的降温值，工作量相对较小。故对于大型箱梁结构，采用降温法更为适宜。

降温法的原理是利用温度变化产生的线应变等于轴力产生的线应变，即。则所需降温值，其中，Δt为所需施加的降温值;A为预应力筋截面面积;α为预应力筋线膨胀系数;E为预应力筋弹性模量。

能够反映预应力损失是降温法的优点，但确定有效预应力的分布却是难点。由于大型箱梁结构中预应力筋数量众多，线形复杂，使得计算各项预应力损失及考虑反摩阻的影响较为困难。鉴于这点，常规办法是采用折减系数来考虑预应力损失，但有效预应力值沿长度不变，这与实际相差较大［2］。针对上述不足，本文提出引入平面杆系计算结果来准确确定力筋中的有效预应力分布。即建立与实体模型完全相同的平面杆系模型，精确算出各项预应力损失。由于实体模型能够考虑徐变收缩引起的预应力损失，故计算有效预应力时只需考虑摩擦损失、锚具变形和预应力筋回缩引起的损失、混凝土弹性压缩引起的损失及预应力筋松弛引起的损失。需要说明的是，预应力筋松弛引起的损失是随时间发展的，模型难以模拟，故简化为一次性扣除。下面以某连续刚构为背景工程，将上述两种方法进行对比分析。

2 实例分析

2．1 连续刚构构造

该桥为双薄壁墩连续刚构桥，跨径140 m+268 m+140 m=548 m。主梁为分离式单箱单室直腹板箱梁，单幅箱梁顶宽16．4 m，梁底宽7．5 m。箱梁梁高及底板厚度均按1．6次抛物线变化。桥墩处梁高15．0 m，跨中梁高4．5 m。主梁采用三向预应力体系:纵、横向预应力采用钢绞线，竖向预应力采用精轧螺纹粗钢筋。主梁采用C60混凝土。主梁一般构造见图1［3］。

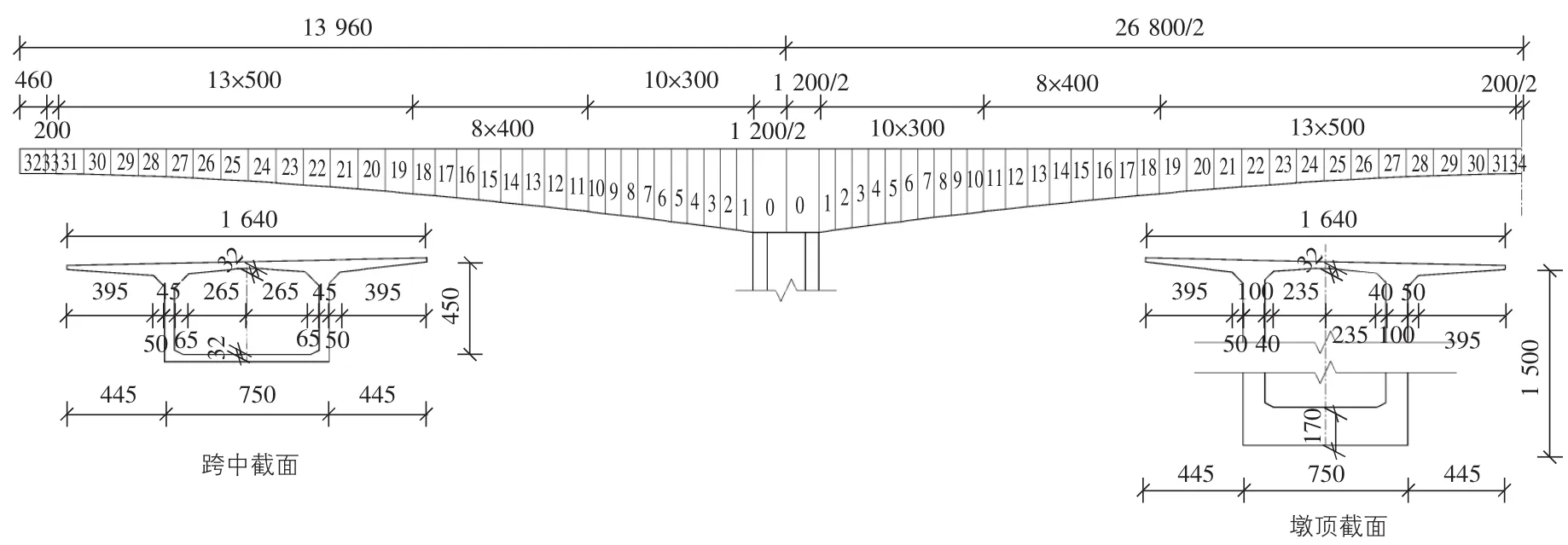
图1 主梁一般构造图

2．2 有限元模型

计算分析采用MIDAS有限元分析程序。实体模型和平面杆系模型说明如下。1)平面杆系模型。依据施工过程，进行平面杆系模型的单元划分。主梁与墩身采用刚性连接。模型的边界条件符合实际情况，双薄壁墩的墩底采用固定约束，边支座采用单向约束。2)空间实体模型。由于只分析永久作用，利用结构的对称性，选取纵向1/2结构建立空间实体单元和梁单元组合的有限元模型，模拟真实的悬臂浇筑施工过程。中跨混凝土箱梁采用8节点的实体单元模拟，少量位置采用6节点实体单元模拟，边跨混凝土箱梁采用梁单元模拟。在薄壁墩处实体单元和梁单元连接的地方，设一块大刚度零重量的虚拟刚性板。纵向、竖向以及横向预应力筋采用梁单元模拟，预应力效应通过降温法模拟。引入平面杆系模型的计算结果确定有效预应力分布。模型的边界条件符合实际情况，双薄壁墩的墩底采用固定约束，边支座采用双向约束，中跨跨中采用纵向对称约束。图2和图3分别为空间实体有限元模型和几何模型的示意图。

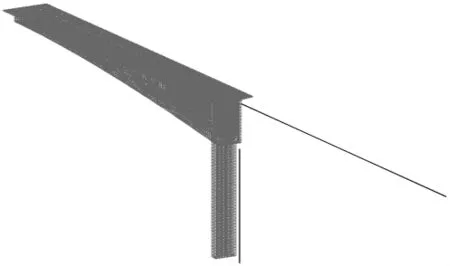
图2 空间实体有限元模型示意图

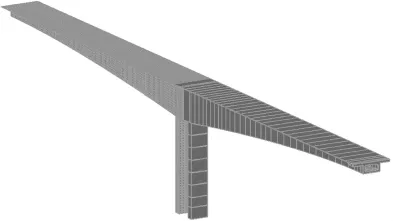
图3 空间实体几何模型示意图

2．3 两种方法的对比分析

1)钢束有效预应力值差异。结构中F31号预应力筋长度最大，线形最复杂，有效预应力值分布变化最大，故以其进行有效预应力值比较。图4，图5分别给出了两种方法在成桥初期和成桥30年两个阶段钢束中有效预应力的比较。图中标注C的曲线表示采用常规折减系数法的计算结果，标注X的曲线表示采用引入平面杆系计算结果方法的计算结果。由图4，图5不难看出两种方法下钢束中有效预应力存在着明显差异，且这种差异随着远离张拉端而逐渐增大。表1给出了这种差异的具体值。

图4 成桥初期钢束应力值比较示意图

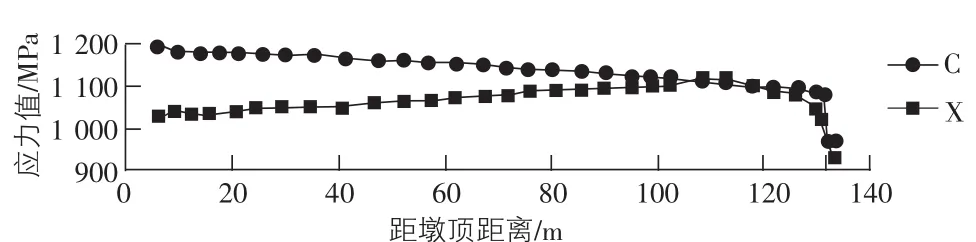
图5 成桥30年钢束应力值比较示意图

从图4，图5以及表1可以看出两种方法计算得到的钢束有效预应力值存在着很大的差异，采用常规折减系数法得到的钢束有效预应力值与实际情况有较大的差异，这种差异应引起重视。

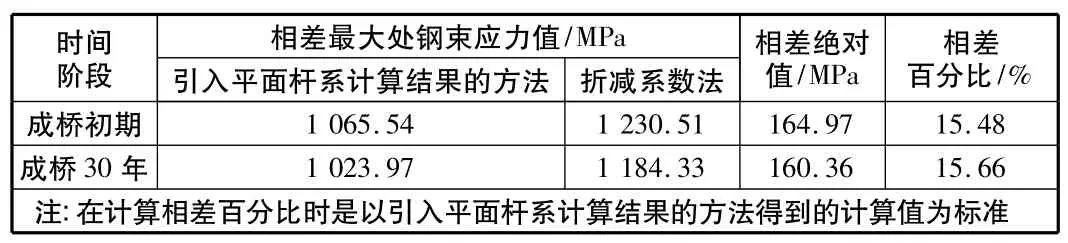
表1 钢束有效预应力最大差值比较

2)结构受力特性差异。通过比较关键截面的应力来说明。关键截面选取跨中截面和薄壁墩外侧截面进行对比。图6，图7给出了两种计算方法得到的上述两截面的法向应力云图(限于篇幅这里只给出成桥初期应力云图，其中a)为引入平面杆系计算结果的方法，b)为常规折减系数法)。

图6 薄壁墩外侧截面成桥初期法向应力云图

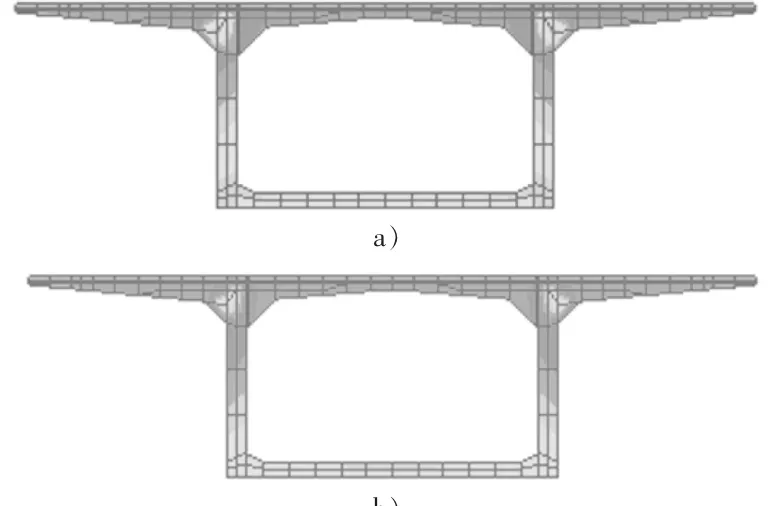
图7 跨中截面成桥初期法向应力云图

由图6，图7可以看出两种方法得到的应力云图存在明显差异，应力值相差较大，应力分布规律也完全不同。以薄壁墩外侧截面成桥初期法向应力为例:a)方法得到的截面法向应力为－4．39 MPa～ － 17．68 MPa，b)方法得到的截面法向应力为－5．16 MPa～ －20．28 MPa;底板内应力分布，a)呈环状分布，中心约为 12．5 MPa，外围约为 11．04 MPa，b)分布比较均匀，约为9．36 MPa，仅在最下缘有很小一部分约为7．36 MPa。

3 结语

通过上述对比分析，可以看出常规折减系数法与实际情况存在较大的差异，且这种差异较难减小到可接受的范围内，因此对于大型箱梁结构的空间分析采用折减系数法是不妥当的。本文提出的引入平面杆系计算结果的方法修正上述不足，真实反映了钢束中有效预应力的分布，准确反映了预应力对结构的空间效应。该方法建模工作量增加不大，但结果精确度有较大提高。需要说明的是，本文在采用引入平面杆系计算结果的方法时，平面杆系模型的单元划分是依据悬臂施工的节段长度而定的，如果进一步细分单元将得到更精确的钢束有效预应力分布。

［1］同济大学桥梁工程系．大跨径连续刚构桥箱梁抗裂性能研究［D］．上海:同济大学，2005．

［2］李国平．预应力混凝土结构设计原理［M］．北京:人民交通出版社，2000．

［3］高 金．预应力对箱梁抗剪承载能力的影响分析［D］．上海:同济大学硕士学位论文，2005．