通过差分非高斯操作连续变量量子密钥分发

王 硕， 王 萍， 郭 迎， 王兴华

（1．中南大学 信息科学与工程学院， 湖南 长沙410083；2．怀德第一中学， 吉林 公主岭136100）

通过差分非高斯操作连续变量量子密钥分发

王 硕1， 王 萍1， 郭 迎1， 王兴华2

（1．中南大学 信息科学与工程学院， 湖南 长沙410083；2．怀德第一中学， 吉林 公主岭136100）

人们发现非高斯操作可以用来提升高斯纠缠态的的纠缠度，本文提出了一种通过使用非高斯差分操作来进行放射性的基于纠缠(Entanglement-based,EB)的连续变量量子密钥分发(CVQKD)的方法，其中纠缠源产生于中间而不是合法的通信两端.这个被提出的放射性的结构方案对分析在有损信道中光子如何丢失是非常有用的，这种分析可以提高量子通信的性能.它可以在当前技术条件下实现.为了提高通信的安全距离和基于EB协议和PM协议的噪声容限，这个技术采用一种在色散潮流中新的成熟的和通用的非高斯操作.

量子密钥分发；连续变量；非高斯操作；光子减法

量子密钥分发通常为两个远距离参与者，Alice和Bob提供一种方法，来建立一个安全密钥序列[1].其中存在三个主要的标准来衡量一个量子密钥分发方案，即为：实用性，性能和安全性[2].

连续变量量子密钥分发通过光子场x和p的正交性进行编码并使用零差或外差检测来提取它，对于最初选择离散变量量子密钥分发是因为它提供更高的检测效率，现成的激光源和更加方便地集成到当前的通信系统.在过去的十年中连续变量量子密钥分发已经产生重大进展.许多最近的成果包括无条件的安全性证明抵抗任意潜在攻击策略[4]，以及基于纠缠的连续变量量子密钥分发试验性的展示[5]和改进的调制[6]或者具有高效率甚至在低信噪比中解码[7].然而，安全性分析过多的依赖于量子信道是线性的假设[7].最近，Guo以及其他人已经提出一个改进四态EB CVQKD方案，其中合法参与者在信道不是线性的假设下计算出协方差矩阵[8].不幸的是，这两个合法通信端正交的相关性不能达到一个EPR态，这明显的限制了实际运用中的CVQKD的密钥率.

有趣是，它已经被从理论和实践上证明了非高斯操作[9]如光子减法和光子加法运算，可以被用来增加和提高在高斯纠缠态的纠缠度[10]，由此提高量子线性放大器[11]和量子通信的性能[12].在本文中，我们关注在非高斯态操作基础上的一种放射性的EB CVQKD的设计,从而提高系统性能，这种非高斯操作即为：减法运算.其中的纠缠源通过一个中立的通信端Fred而放射的,来自中心的窃听者Eve位于Fred和合法参与者之间，其目的是为了完全控制高斯纠缠态.它通过使用原始的分析技术[13]表明非高斯差分可以在当前技术下[3]实践中实现，也可以增加在合法参与者之间正交的相关性.这个协方差矩阵可以在不使用线性信道的假设下的实验数据中直接评估.相应的，它对应的制备与测量方案在当前的技术下是不难实现的.它允许在长距离的情况下密钥的分发还是有好的抵抗与最初高斯调制有关的额外噪声性能，这也说明了这个方案和原始的方案的不同，尤其是，在研究非理想的信道中光子丢失对连续变量量子密钥分发的性能产生的影响.

本文的结构如下，第二部分致力于通过差分的非高斯操作进行放射性的连续变量量子密钥分发方法的基础结构.第三部分证明提出的EB CVQKD的密钥率，它位于中间的窃听者是基于传统的分析技术.最后在第四部分得出结论.

1 非高斯操作下的放射性的EB CVQKD

这个提出的连续变量量子密钥分发可以在制备与测量方案中实施，为了使理论分析简单一些，我们认为它的效率等价于使用高斯调制的基于纠缠方案[4].以设计一个放 射的基于纠缠的连续变量量子密钥分发方案为开始，它对于理解一个使用高斯调制的传统的EB CVQKD协议是很有帮助.通过中立参与者，Fred，一个纠缠的高斯源，在两个远距离参与者之间的建立起纠缠源，Alice和Bob，为了在一个放射的量子网络中（例如下图1）产生一个密钥率加密.

图1 非高斯操作下的放射性的EB CVQKD的原理示意图.在这里的PNRD代表光子数分辨探测器

假设Fred准备了一个双模真空压缩态ρab，具有方差V0+1，其中V0=2α2代表调制方差.态ρab的一半发送给Alice同时另外一半的态通过具有传送效率T和额外噪声ε的光子信道发送给Bob.在Alice（或者Bob）接收这个态时，她（或者他）就使用一个理想探测器选择外差或者零差探测器来检测.同时，我们假设Alice当Bob应用零差或者外差检测时采用外差检测，这是为了共享两个相关的高斯变量从而可以被进一步用于提取私钥加密.因为实际的量子信道和探测器并不是理想的，增加的信道噪声被指为信道输入记为Xline=1/T-1+ε.

我们想到的是考虑到一个在非高斯操作下非高斯操作下的EB CVQKD通过光子减法操作来实现.如上图1所示，Fred首先为了每一个模结合一个分束器和一个光子数分辨探测器.在两个光线在模式a0和b0同时的被两个具有相同传输器的分束器所利用之后，例如：μa=μb=μ，结果态可以被表示为：

其中pk代表归一化因子，纠缠的非高斯态由下式给出：

例如，当k∈{1,2}，它可以由下面的式子计算得出：

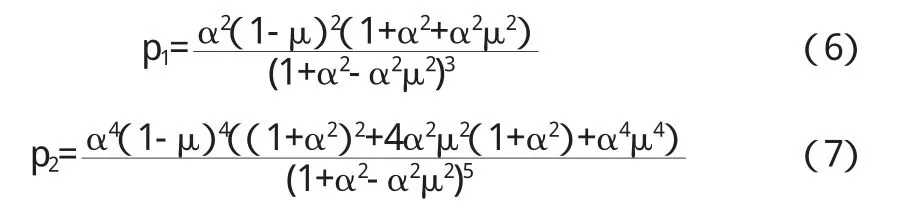
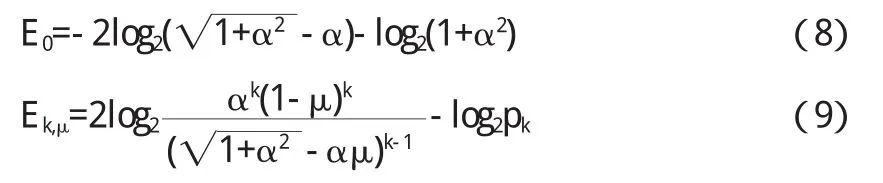
我们注意前面所提到的减法操作对于μ=1是不存在的.很容易的证明，光子k态在k≥1时，比原始的输入态有一个更大的纠缠度，如图2表示.有很多的纠缠态使用一个合适的传输条件μ∈(0,1).此外，更大数量的减去光子k意味着双向态的更大的纠缠.它表明基于减法的非高斯操作可以增加双向态的两种模式的相关性.我们也注意光子数分辨探测器应该被作为有效的检测[18]，这导致了一个对纠缠源处理后产生了非高斯混合态.

图2 |φ〉ab和的纠缠比较.这里因为μ∈{0.5,0.8}和k∈{1,2}，所以E0=E(|φ〉ab)和1具有 α∈(0,1)

在下文中，我们尝试证明由Fred所带来的纠缠性能的提高，Fred在传送纠缠态给远距离的参与者之前完成了基于光子减法的非高斯操作，它会提高在放射光子网络中的基于纠缠的连续变量量子密钥分发的性能.

2 放射性的基于纠缠的连续变量量子密钥分发的密钥率

在这部分，我们表明如何估计在基于光子减法的非高斯操作下的放射的EB CVQKD的密钥率.所以我们集中于分析直接协商，因为反向协商可以用类似的方法得到.基于高斯调制的EB CVQKD，这个密钥率可以有下面的式子计算出来[10]：

其中S是冯·诺伊曼熵，ρe是窃听者的局部态，ma代表Alice随着P(ma)的可能性实现的测量结果代表窃听者的辅助态，它是在Alice的测量结果的ma条件下得到的.由

于窃听者可以提供一个Alice的纯态和Bob的密度矩阵，我们得到)和)，如图1所示.因此，Holevo数量可以写为[8]：

而且，根据一个有益的协方差矩阵如下[4]：

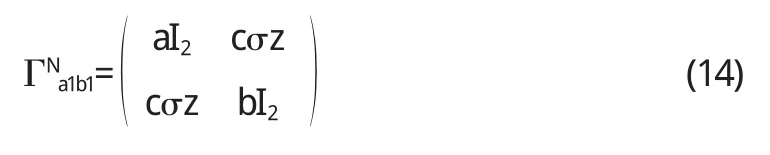
其中I2是2×2的单位矩阵，σz是以1和-1为对角线的对角矩阵，同时a，b和c代表有效的参数，由下面的式子得出：

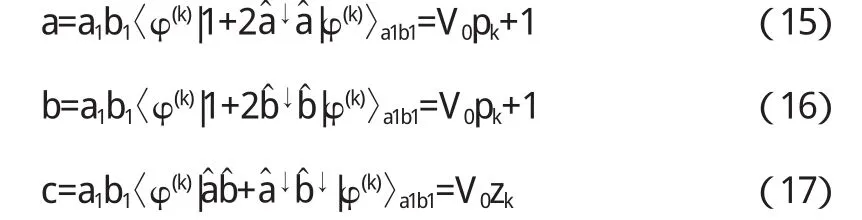
举例，当k=1时，我们得到：

图3 z1和z0的相关性对比.这里z0表示高斯EPR态的关系，同时z1对于随着α∈{0,1}的变化μ∈{0.5,0.8}.

我们注意基于减法的连续变量量子密钥分发当μ=1时不存在，这和原始的具有纠缠源在中间的连续变量量子密钥分发有关.如图3所示，熟悉矩阵的关系对于适当的参数μ和α可以制成比高斯EPR态更大.它表明对于被减去的双向态提出的方案的无条件安全性受μ和α值的限制，当α趋近于0的时候它变成高斯EPR态的下界.然而，当α的值变得非常小的时候，在实际中它就变得无效了.这就是我们在提出的方案中所要完成的不得不选择合适的μ和α值的原因.

因为由窃听者执行的最具有攻击力的策略是高斯攻击，我们假设存在一个等价的高斯态ρa1b1具有相同的协方差矩阵作为以光子减法为基础的基于纠缠的连续变量量子密钥分发，例如和之间的关系在Ref.中被讨论[17].接下来，我们考虑在以代替被减态基础的提出的方案的效率.

假设Alice执行外差检测，通过在一个平衡的分束器中结合她的模和一个真空附属d0来产生一个相干态.在原始态上的交互执行可以被描述为继续通过他的模式采用零差或者外差检测.随后，为了零差检测在Alice和Bob之间共享的信息可由下式计算得出：

外差检测由下式给出：

接下来，我们考虑的是计算窃听者和Alice的的共有信息，例如作为Alice零差测量的条件.使用提纯方法，我们有，它是相关的方差矩阵的辛本征值λ3,4的函数，具体式子如下：

注意到一个外差检测在本质上是一个通过相干态的推测，外差测量结果在协方差矩阵中如下：

然后，辛本征值直接的表示为：

因此，通过外差检测的冯·诺伊曼熵就可以如下表示了：

由此，对于基于光子减法的放射性的连续变量量子密钥率的下界由下式给出：

其中pk代表了在非高斯操作下成功实施的可能性.也就是，零差检测下的密钥率由下式计算出来：

同时外差检测由下式得出：

在放射的基于纠缠的连续变量量子密钥分发在光子信道中不具有非高斯操作，原始的高斯态ρ0的协方差矩阵ΓG

并且协方差矩阵ΓG0的辛本征值再Bob的外差测量上是有条件的：

3 结论

我们提出一个方法来提高在非高斯的操作下的基于纠缠的连续变量量子密钥方案的性能，尤其是，光子减法操作.这个提出的光子减法操作在当前的技术下很容易的实现.由于被调制的态是非高斯的，我们预测出密钥率和信道过剩噪声的可容忍度在高斯定理的协助下对抗一般的集体攻击.结果表示这个提出的方案比原始的方案允许更长的安全距离，并且在抵抗信道过剩噪声中有更好的性能.此外，因为可用的调制方差VA的区域可以是开放的，所以这个提出的方案有一个更加灵活的应用.而且，我们表明减法操作也可能等同于准备—措施方案.总之，我们已经证明光子减法不仅能被用于提高量子态的纠缠度，也能提高连续变量量子密钥分配的性能，包括更长的安全距离，更大的过剩噪声可容忍度，和更加灵活的调制方差的选择.

〔1〕M.N ielsen,and I.Chuang,Quantum computation and quantum information(Cambridge University Press, Cambridge,2000).

〔2〕V.Scarani,H.Bechmann-Pasquinucci,N.J.Cerf,M. Dusek,N.Lutkenhaus,and M.Peev,Rev.Mod.Phys. 81,1301(2009).

〔3〕C.W eedbrook,S.Pirandola,R.Garcaa-Patraon,N.J. Cerf,T.C.Ralph,J.H.Shapiro,and S.Lloyd,Rev. Mod.Phys.84,621(2012).

〔4〕R.Garcia-Patron and N.J.Cerf,Phys.Rev.Lett. 97,190503(2006).190503(2006).

〔5〕L.S.Madsen,V.C.Usenko,M.Lassen,R.Filip,and U.L.Andersen,Nat.Commun.3,1083(2012).

〔6〕A.Leverrier and P.Grangier,Phys.Rev.Lett. 102,180504(2009).

〔7〕P.Jouguet,S.Kunz-Jacques,and A.Leverrier,Phys. Rev.A 84,062317(2011).

〔8〕J.Yang,B.Xu,and H.Guo,Phys.Rev.A 86, 042314(2012).

〔9〕H.Takahashi,J.S.Neergaard-N ielsen,M.Takeuchi, M.Takeoka,K.Hayasaka,A.Furusawa,and M.Sasaki, Nature Photon.4,178(2010).

〔10〕A.Leverrier and P.Grangier,Phys.Rev.A 83, 042312(2011).

〔11〕H.-J.Kim,S.-Y.Lee,S.-W.Ji,and H.Nha,Phys. Rev.A 85,013839(2012).

〔12〕S.-Y.Lee,S.-W.Ji,H.-J.Kim,and H.Nha,Phys. Rev.A 84,012302(2011).

〔13〕R.Garcia-Patron,Ph.D.thesis,Universitfle Libre de Bruxelles,2007.

〔14〕A.Peres,Phys.Rev.Lett.77,1413(1996).

〔15〕G.Vidal and R.F.W erner,Phys.Rev.A 65,032314 (2002).

〔16〕C.Weedbrook,Phys.Rev.A 87,022308(2013).

〔17〕F.Grosshans,N.J.Cerf,J.W enger,R.Tualle-Brouri, and P.Grangier Quantum Infor.Comput.3,535 (2003).

〔18〕A.Kitagawa,M.Takeoka,M.Sasaki,and A.Chefles, Phys.Rev.A 73,042310(2006).

O141

A

1673-260X（2014）07-0017-04