Probability Inequalities for Extended Negatively Dependent Random Variables and Their Applications

TANG Xiao-feng

(School of Mathematics and Computational Science,Fuyang Teacher’s College,Fuyang 236041,China)

Probability Inequalities for Extended Negatively Dependent Random Variables and Their Applications

TANG Xiao-feng

(School of Mathematics and Computational Science,Fuyang Teacher’s College,Fuyang 236041,China)

Some probability inequalities are established for extended negatively dependent (END)random variables.The inequalities extend some corresponding ones for negatively associated random variables and negatively orthant dependent random variables.By using these probability inequalities,we further study the complete convergence for END random variables.We also obtain the convergence rate O(n-1/2ln1/2n)for the strong law of large numbers,which generalizes and improves the corresponding ones for some known results.

extended negatively dependent sequence;negatively orthant dependent sequence;probability inequality;complete convergence

§1.Introduction

Firstly,let us recall the concept of extended negatively dependent random variables.

Def i nition 1.1[1]We call random variables{Xn,n≥1}extended negatively dependent (END,in short)if there exists a constant M＞0 such that both

and

hold for each n≥1 and all real numbers x1,x2,···,xn.

If M=1,the random variables are called negatively orthant dependent(NOD,in short). For more details about NOD random variables,one can refer to Joag-Dev and Proschan[2], Want et al[34],Sung[5],Wu[6],and so forth.The concept of END sequence was introduced by Liu[1].Some applications for END sequence have been found.See for example,Liu[1]obtained the precise large deviations for dependent random variables with heavy tails,Liu[7]studied the sufficient and necessary conditions of moderate deviations for dependent random variables with heavy tails,Chen et al[8]for obtained the strong law of large numbers for END random variables,Shen[9]presented some probability inequalities for END sequence and gave some applications,Wang and Wang[10]investigated the extended precise large deviations of random sums in the presence of END structure and consistent variation,and so forth.It is easily seen that independent random variables and NOD random variables are END.Joag-Dev and Proschan[2]pointed out that NA random variables are NOD.Thus,NA random variables are END.Since END random variables are much weaker than independent random variables,NA random variables and NOD random variables,studying the limit behavior of END sequence is of interest.

It is well known that the probability inequality plays an important role in various proofs of limit theorems.We consider the following probability inequality.For proof,one can refer to Hoef f ding[11].

Theorem AIf X1,X2,···,Xnare independent and ai≤Xi≤bi(i=1,2,···,n), then for any t＞0,

Since then the inequality was extended to some cases of dependent sequences,such as negatively associated(NA,in short)sequence,negatively orthant dependent(NOD,in short)sequence,and so forth.The main purpose of the paper is to extend Theorem A for independent sequence to the case of extended negatively dependent(END)sequence,which contains independent sequence, NA sequence and NOD sequence as special cases.By using the Hoef f ding-type inequality,we further study the complete convergence and strong law of large numbers for END sequence.We obtain the convergence rate O(n−1/2ln1/2n)for the strong law of large numbers,which generalizes and improves the corresponding ones of Kim and Kim[12],Nooghabi and Azarnoosh[13], Xing et al[14]and Jabbari et al[15].

The following lemmas will be used to prove the main results of the paper.

Lemma 1.1[7]Let random variables X1,X2,···,Xnbe END.

(i)If f1,f2,···,fnare all nondecreasing(or nonincreasing)functions,then random variables f1(X1),f2(X2),···,fn(Xn)are END.

(ii)For each n≥1,there exists a constant M＞0 such that

Lemma 1.2If X is a random variable such that a≤X≤b,where a and b are f i nite real numbers,then for any real number h,

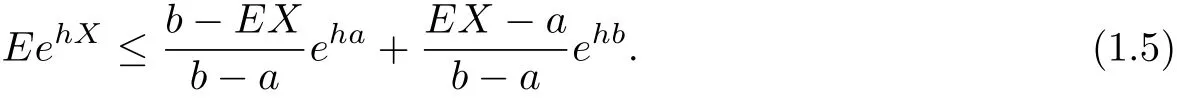
ProofSince the exponential function exp(hX)is convex,its graph is bounded above on the interval a≤X≤b by the straight line which connects its ordinates at X=a and X=b. Thus

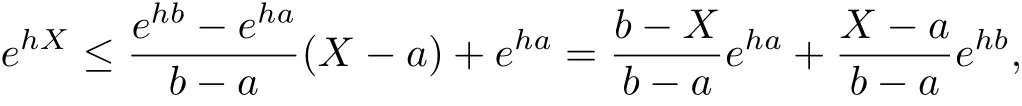
which implies(1.5).

Throughout the paper,let{Xn,n≥1}be a sequence of random variables def i ned on a f i xed probability space(Ω,F,P).Denotefor each n≥1.M denotes a positive constant which may be dif f erent in various places.

§2.Main Results and Their Proofs

Theorem 2.1Let{Xn,n≥1}be a sequence of END random variables.If there exist two sequences of real numbers{an,n≥1}and{bn,n≥1}such that ai≤Xi≤bifor each i≥1,then for any ε＞0 and each n≥1,there exists a constant M＞0 such that

ProofFor any h＞0,by Markov’s inequality,we can see that

It follows from Lemma 1.1(ii)that there exists a constant M＞0 such that

where

The f i rst two derivatives of L(hi)are

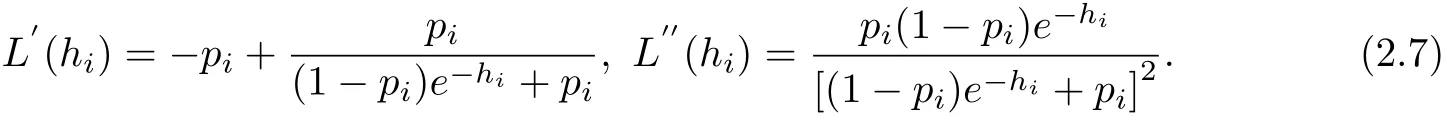
The last ratio is of the form u(1−u),where 0＜u＜1.Hence

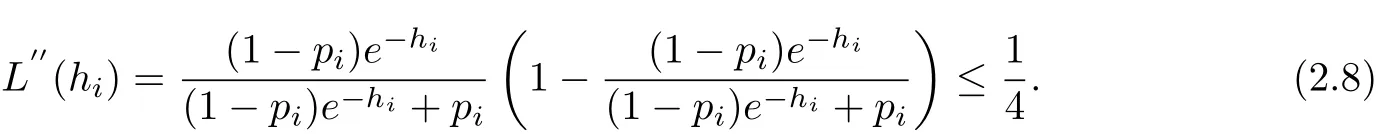
Therefore,by Taylor’s formula and(2.8),we can get

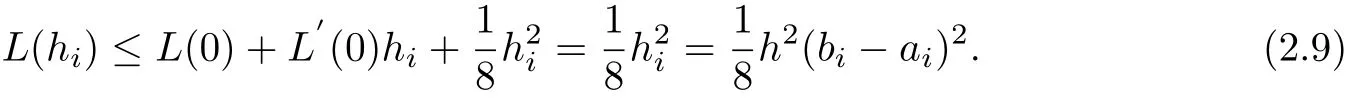
It follows from(2.6)and(2.9)that

By(2.4),(2.5)and(2.10),we have

It is easily seen that the right-hand side of(2.11)has its minimum at hInserting this value in(2.11),we can obtain(2.1)immediately.Since{−Xn,n≥1}is a sequence of END random variables,(2.1)implies(2.2).(2.1)and(2.2)yield(2.3).The proof is complete.

Corollary 2.1Let{Xn,n≥1}be a sequence of END random variables with common distribution function F.Then for any ε＞0 and any x∈ℝ,there exists a constant M＞0 such that

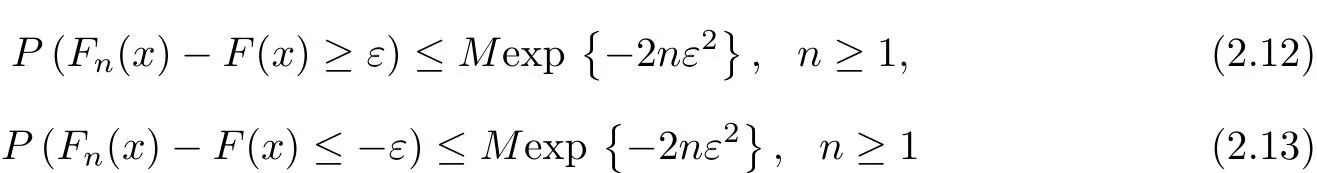
and

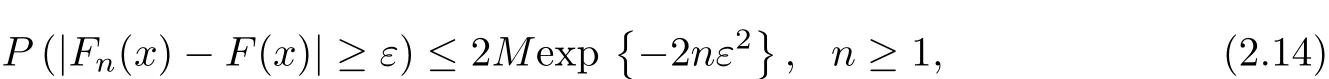
ProofFor f i xed x,by Lemma 1.1(i),it is easily seen that{I(Xn≤x),n≥1}is a sequence of END random variables satisfying 0≤I(Xn≤x)≤1,n≥1 and E(Fn(x))=F(x). Therefore,(2.12)∼(2.14)follow from Theorem 2.1 immediately.

Corollary 2.2Under the conditions of Corollary 2.1,Fn(x)→F(x)completely for any x∈ℝ.

Theorem 2.2Let{Xn,n≥1}be a sequence of END random variables with|Xi|≤c＜∞for each i≥1,where c is a positive constant.Then for any r＞

ProofFor any ε＞0,it follows from Theorem 2.1 that

which implies(2.15).

Theorem 2.3Let{Xn,n≥1}be a sequence of END random variables with EXn=0 for each n≥1.If there exists a sequence of positive numbers{cn,n≥1}such that|Xi|≤cifor each i≥1,then for any t＞0 and n≥1,there exists a constant M＞0 such that

ProofIt is easy to check that for all x∈ℝ,the following inequality holds

Thus,by EXi=0 and|Xi|≤cifor each i≥1,we have

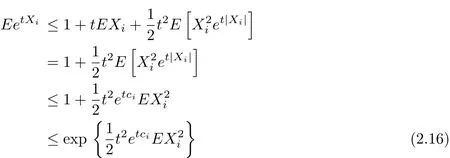
for any t＞0.By Lemma 1.1 and(2.16),there exists a constant M＞0 such that

This completes the proof of the theorem.

Corollary 2.3Let{Xn,n≥1}be a sequence of END random variables such that |Xi|≤cifor each i≥1,where{cn,n≥1}is a sequence of positive numbers.Then for any t＞0 and n≥1,there exists a constant M＞0 such that

ProofIt is easily seen that{Xn−EXn,n≥1}is a sequence of END random variables with E(Xi−EXi)=0 and|Xi−EXi|≤2cifor each i≥1.By Theorem 2.3,there exists a

constant M＞0 such that

The proof is complete.

Similarly,we can get the following corollary.

Corollary 2.4Let{Xn,n≥1}be a sequence of END random variables such that |Xi|≤cnfor each 1≤i≤n,n≥1,where{cn,n≥1}is a sequence of positive numbers.Then for any t＞0 and n≥1,there exists a constant M＞0 such that

Theorem 2.4Let{Xn,n≥1}be a sequence of END random variables such that|Xi|≤cnfor each 1≤i≤n,n≥1,where{cn,n≥1}is a sequence of positive numbers.Then for any ε＞0 such that ε≤e(2cn)and n≥1,there exists a constant M＞0 such that

ProofBy Markov’s inequality and Corollary 2.4,we have that for any t＞0,there exists a constant M＞0 such that

Corollary 2.5Let{Xn,n≥1}be a sequence of identically distributed END random variables.Assume that there exists a positive integer n0such that|Xi|≤cnfor each 1≤i≤n, n≥n0,where{cn,n≥1}is a sequence of positive numbers.Then for any ε＞0 such that ε≤eEX21/(2cn)and n≥n0,there exists a constant M＞0 such that

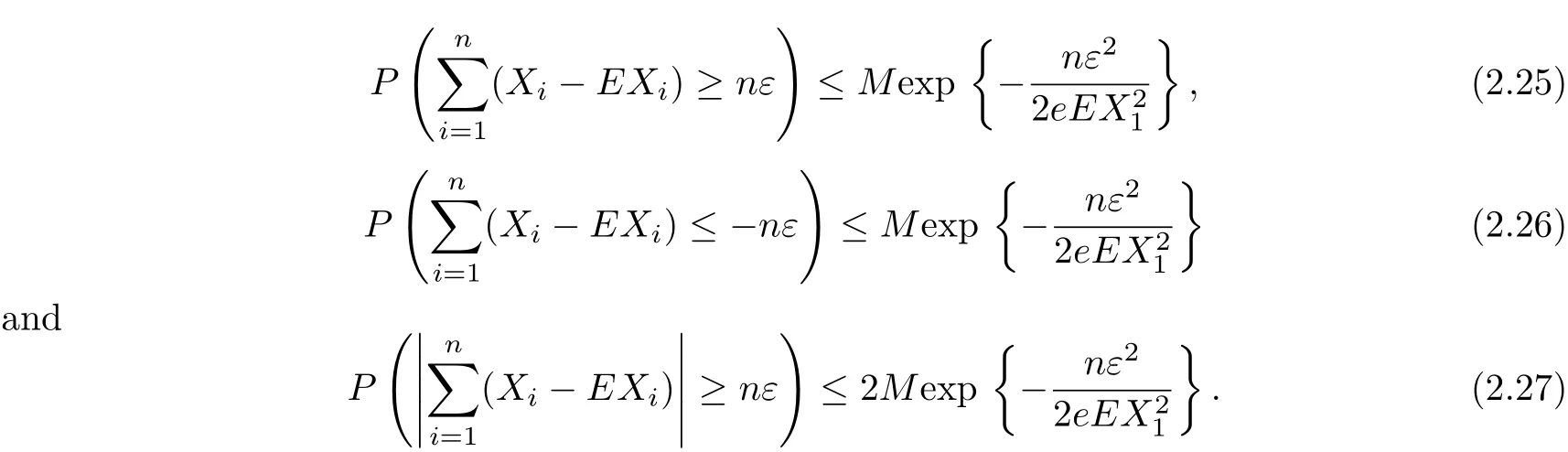
Theorem 2.5Let{Xn,n≥1}be a sequence of identically distributed END random variables.Assume that there exists a positive integer n0such that|Xi|≤cnfor each 1≤i≤n, n≥n0,where{cn,n≥1}is a sequence of positive numbers satisfying

Denote εn=.Then for n≥n0,there exists a constant M＞0 such that

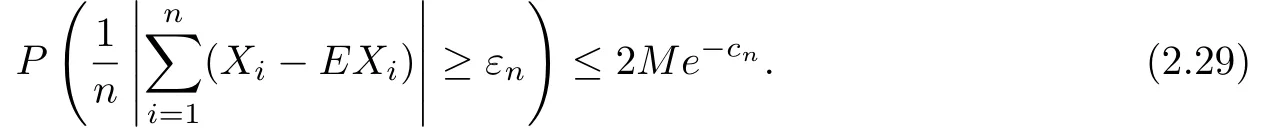
ProofIt is easy to check thatIt follows from Corollary 2.5 that for n≥n0,there exists a constant M＞0 such that

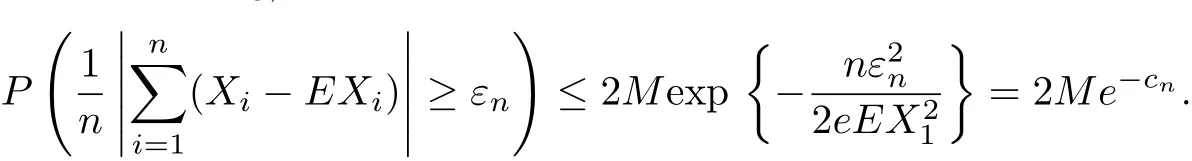
The proof is complete.

Taking cn=δ lnn and δ＞1 in Theorem 2.5,we can get the following result.

Theorem 2.6Let{Xn,n≥1}be a sequence of identically distributed END random variables.Assume that there exists a positive integer n0such that|Xi|≤δ lnn for each 1≤i≤n,n≥n0and some δ＞1.

Remark 2.1Borel–Cantelli lemma implies thaconverges almost surely with growth rate O(n−1/2ln1/2n)under the conditions of Theorem 2.6,which generalizes and improves the corresponding ones of Kim and Kim[12],Nooghabi and Azarnoosh[13],Xing et al[14]and Jabbari et al[15].

[References]

[1]LIU Li.Precise large deviations for dependent random variables with heavy tails[J].Statistics and Probability Letters,2009,79:1290-1298.

[2]JOAG-DEV K,PROSCHAN F.Negative association of random variables with applications[J].The Annals of Statistics,1983,11(1):286-295.

[3]WANG Xue-jun,HU Shu-he,YANG Wen-zhi,et al.Exponential inequalities and inverse moment for NOD sequence[J].Statistics and Probability Letters,2010,80:452-461.

[4]WANG Xue-jun,HU Shu-he,SHEN Ai-ting,et al.An exponential inequality for a NOD sequence and a strong law of large numbers[J].Applied Mathematics Letters,2011,24:219-223.

[5]SUNG S H.On the strong convergence for weighted sums of random variables[J].Statistical Papers,2011, 52:447-454.

[6]WU Qun-ying.A complete convergence theorem for weighted sums of arrays of rowwise negatively dependent random variables[J].Journal of Inequalities and Applications,2012,2012:50,doi:10.1186/1029-242X-2012-50.

[7]LIU Li.Necessary and sufficient conditions for moderate deviations of dependent random variables with heavy tails[J].SCIENCE CHINA Mathematics,2010,53(6):1421-1434.

[8]CHEN Yi-qing,CHEN An-yue,NG K W.The strong law of large numbers for extend negatively dependent random variables[J].Journal of Applied Probability,2010,47:908-922.

[9]SHEN Ai-ting.Probability inequalities for END sequence and their applications[J].Journal of Inequalities and Applications,2011,2011:98.

[10]WANG Shi-jie,WANG Wen-sheng.Extended precise large deviations of random sums in the presence of END structure and consistent variation[J].Journal of Applied Mathematics,2012,Volume 2012,Article ID 436531,12 pages,doi:10.1155/2012/436531.

[11]HODFFDING W.Probability inequalities for sums of bounded random variables[J].Journal of the American Statistical Association,1963,58(301):13-30.

[12]KIM T S,KIM H C.On the exponential inequality for negative dependent sequence[J].Communications of the Korean Mathematical Society,2007,22(2):315-321.

[13]NOOGHABI H J,AZARNOOSH H A.Exponential inequality for negatively associated random variables[J]. Statistical Papers,2009,50(2):419-428.

[14]XING Guo-dong,YANG Shan-chao,LIU Ai-lin,et al.A remark on the exponential inequality for negatively associated random variables[J].Journal of the Korean Statistical Society,2009,38:53-57.

[15]JABBARI H,JABBARI M,AZARNOOSH H A.An exponential inequality for negatively associated random variables[J].Electronic Journal of Statistics,2009,3:165-175.

tion:60E15,60F15

O211.4Document code:A

1002–0462(2014)02–0195–08

date:2012-06-08

Supported by the Project of the Feature Specialty of China(TS11496);Supported by the Scientif i c Research Projects of Fuyang Teacher’s College(2009FSKJ09)

Biography:TANG Xiao-feng(1978-),male,native of Fuyang,Anhui,a lecturer of Fuyang Teacher’s College, M.S.D.,engages in probability limit theorem.