Cyclic Codes overF2+uF2+vF2
LIU Xiu-sheng,LIU Hua-lu
(School of Mathematics and Physics,Hubei Polytechnic University,Huangshi 435003,China)
Cyclic Codes overF2+uF2+vF2
LIU Xiu-sheng,LIU Hua-lu
(School of Mathematics and Physics,Hubei Polytechnic University,Huangshi 435003,China)
We study the structure of cyclic codes of an arbitrary length n over the ring F2+uF2+vF2,which is not a f i nite chain ring.We prove that the Gray image of a cyclic code length n overF2+uF2+vF2is a 3-quasi-cyclic code length 3n overF2.
linear codes;cyclic codes;Gray map
§1.Introduction
Cyclic codes over f i nite rings are important class of codes from a theoretical and practical viewpoint.It has been shown that certain good nonlinear binary codes such as binary Kerdock codes are the Gray images of someℤ4-linear codes[3].Using the Gray map a new set of linear or nonlinear binary codes has been constructed as the Gray images of some codes over rings[47]. Recently,cyclic codes over ringF2+uF2+vF2+uvF2have been considered by Yildiz and Karadeniz in[2],where some good binary codes have been obtained as the images under two Gray maps.Some results related to cyclic codes overF2+vF2were given by Zhu et al in[4], where cyclic codes over the ring are principally generated.
In this work,we focus on codes over the ringF2+uF2+vF2,where u2=uv=vu=0 and v2=v.First,we def i ne the Gray map fromF2+uF2+vF2toF2and prove that the image of a linear code of length n overF2+uF2+vF2under the Gray map is a distance-invariant linear code of length 3n overF2.Next,we determine the generator polynomials of such cyclic codes overF2+uF2+vF2and prove that the images under Gray maps of cyclic codes over F2+uF2+vF2are 3-quasic-cyclic codes overF2.
§2.Linear Codes over the RingF2+uF2+vF2
The ringF2+uF2+vF2is def i ned as a characteristic 2 ring subject to the restrictions u2=uv=vu=0 and v2=v.The ideals can be described as
where Iu={0,u},Iv={0,v},Iu+v={0,u,v,u+v},I1+v={0,u,1+v,1+u+v}.
One can see thatF2+uF2+vF2is the principal ring.Another nice observation about this ring is that if a∈F2+uF2+vF2is any element,then

Let WLbe the Lee weight of the element overF2+uF2+vF2and WHbe the ordinary Haming weight for the binary codes,an so we set
∀a,b,c∈F2.The def i nition of the weight immediately leads to a Gray map fromF2+uF2+ vF2towhich can naturally be extended to(F2+uF2+vF2)n
Note that ϕ extends to a distance-preserving isometry
Theorem 1If C is a linear code overF2+uF2+vF2of length n,size 2kand minimum Lee weight d,then ϕ(C)is a binary linear code with parameters[3n,k,d].
Theorem 2Let C⊥be the dual code of C.Then ϕ(C⊥)=ϕ(C)⊥.Moreover,if C is a self-dual code,so is ϕ(C).
ProofFor any c1=a1+ub1+vd1∈C⊥,c2=a2+ub2+vd2∈C,where a1,b1,d1,a2,b2, d2∈.Since c1·c2=0,that is to say
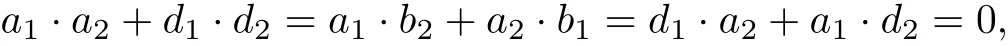
we can obtain that
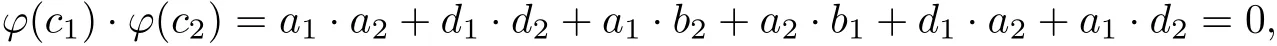
which means ϕ(C⊥)⊆ϕ(C)⊥.By Theorem 1,ϕ(C)is a binary linear code of length 3n of size |C|.So,by the usual properties of the dual of binary codes,we know that|ϕ(C)⊥|=is a Frobenius ring,we have|C||C⊥|=23n([8]).Hence,this implies |ϕ(C⊥)|=|ϕ(C)⊥|.Therefore,ϕ(C⊥)=ϕ(C)⊥.
§3.Characterization of Cyclic Codes overF2+uF2+vF2
The notions of cyclic shift and cyclic codes are standard for codes over all rings.Brief l y,for any ring R,a cyclic shift on Rnis a permutation T such that
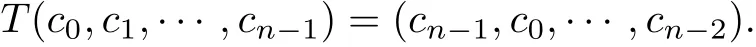
A linear code over ring R of length n is cyclic if it is invariant under cyclic shift.It is known that a linear code over ring R is cyclic if and only if its polynomial representation is an ideal
In the following,we will introduce a homomorphism fromF2+uF2+vF2toF2+uF2and use it to characterize cyclic codes overF2+uF2+vF2by using the results obtained from cyclic codes overF2+uF2.
Start with the homomorphism
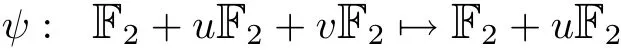
with ψ(a+ub+vd)=a+ub.This homomorphism then can be extended to a homomorphism of rings of polynomials
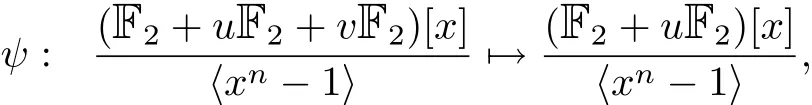
by letting
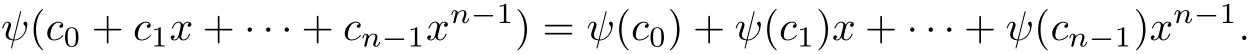
Theorem 3Let C be a cyclic code overF2+uF2+vF2of length n.Then
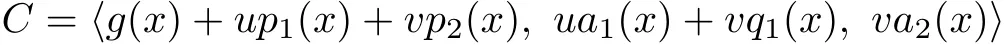
ProofRestrict ψ onto C.Since C is invariant under the cyclic shift,so is ψ(C).This means Im(ψ)is a cyclic code overF2+uF2.By using the characterization in[1],we have

where g,p1,a1are polynomials insatisfying the conditions a1|g|(xn−1),a1(x)|
On the other hand,Ker(ψ)is also a cyclic code over vF2.We can consider it to be v times a cyclic code overF2.By using the characterization[10],we have
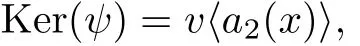
where a2is a polynomial insatisfying the condition a2|(xn−1).Since va1(x)∈ Ker(ψ)=v〈a2(x)〉,a2|a1.
For any f(x)∈C,we can write f(x)=f1(x)+uf2(x)+vf3(x),where f1,f2,f3are polynomials inF2[x].Suppose that
C1={f1(x)+uf2(x)|There exists f3(x)such that f1(x)+uf2(x)+vf3(x)∈C}. Then C1=Im(ψ)=〈g(x)+up1(x),ua1(x)〉.Therefore,we have
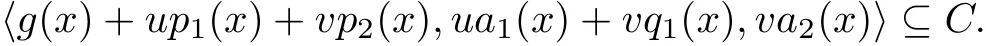
Conversely,for any f(x)∈C,we have f(x)=f1(x)+uf2(x)+vf3(x),where f1(x)+uf2(x) is in C1=〈g(x)+up1(x),ua1(x)〉.Hence there exist c(x),d(x)inF2[x]such that
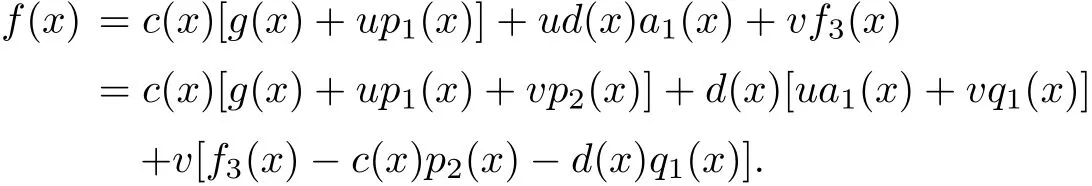
It is easy to see that v[f3(x)−c(x)p2(x)−d(x)q1(x)]∈Kerψ=〈va2(x)〉.Therefore f(x)∈〈g(x)+up1(x)+vp2(x),ua1(x)+vq1(x),va2(x)〉,i.e.,
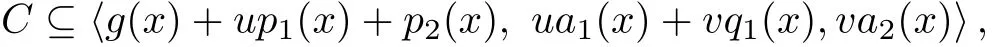
which completes the proof.
Theorem 4Let C be a cyclic code overF2+uF2+vF2of length n for odd n.Then C is an ideal in Rnwhich can be generated by
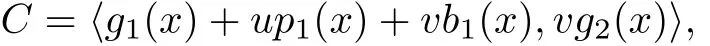
where g1,g2,p1,b1are polynomials insatisfying the conditions p1|g1|(xn−1),g2| (xn−1).
ProofSuppose C is a cyclic code overF2+uF2+vF2of length n for odd n.Then ψ(C) is a cyclic code overF2+uF2and Ker(ψ)is v times a cyclic code of overF2of odd length n. Thus we have

where g1and p1are binary polynomials with p1|g1|(x−1)and

where g2is a binary polynomial with g2|(xn−1).Now combining(3.1)with(3.2)we see that we can write
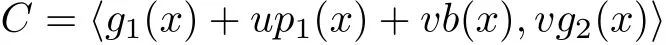
with the same conditions on g1,g2and p1.Now b(x)is a polynomial in.Hence we can write
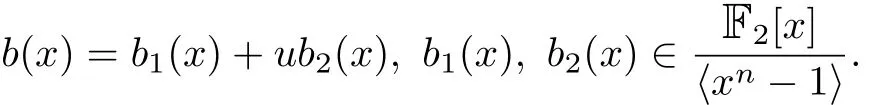
Therefore
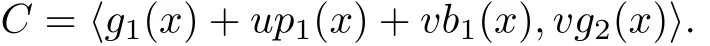
§4.Binary Images of Cyclic Code overF2+uF2+vF2
Before characterizing the binary images of cyclic codes,we recall the def i nition of quasi-cyclic codes.
Def i nition 1Let T be the cyclic shift on(F2+uF2+vF2)n.We say that a linear code C is a s-quasi-cyclic if it is invariable under Ts,i.e.,Ts(C)=C.
Quasi-cyclic codes have been studied extensively in the literature(see[9])and good parameters have been obtained.
Theorem 5Let C be a cyclic code of length n over the ringF2+uF2+vF2.Then ϕ(C) is an 3-quasic-cyclic code of length 3n overF2.
ProofNote that if c=(c0,c1,···,cn−1)∈C with ci=ci0+uci1+vci2for i=0,1,···,n−1,then
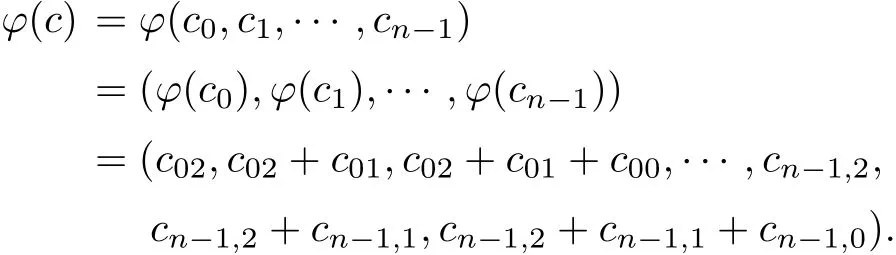
Hence
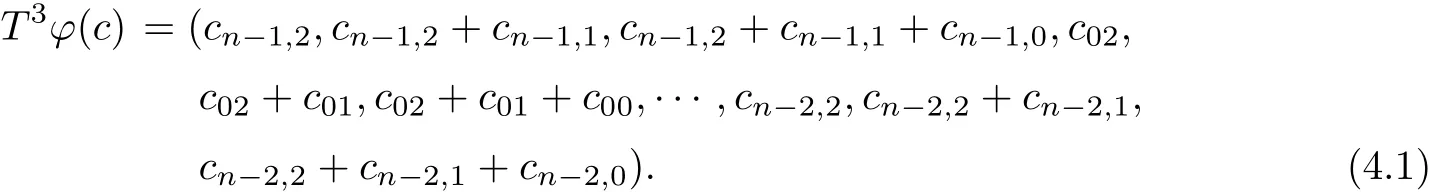
We know that C is a cyclic code overF2+uF2+vF2if and only if T(C)=C.By c=(c0,c1,...,cn−1)∈C,we know T(c)=(cn−1,c0,c1,...,cn−2)∈C.Therefore
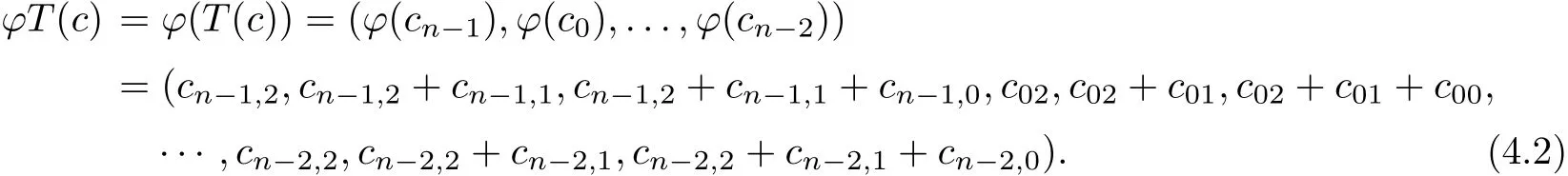
Combining(4.1)with(4.2),we obtain
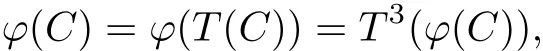
which implies that ϕ(C)is invariant under T3.This proves that ϕ(C)is a 3-quasi-cyclic code of length 3n overF2.
Example 1Let C=〈u+ux+ux2〉be a cyclic code of length 3 overF2+uF2+vF2. Then ϕ(C)is a[9,1,6]-3-quasi-cyclic code overF2.
Example 2Let C=〈u+vx+(u+v)x2〉be a cyclic code of length 3 overF2+uF2+vF2. Then ϕ(C)is a[9,3,3]-3-quasi-cyclic code overF2.
§5.Conclusion
We have characterized cyclic codes overF2+uF2+vF2and proved that the Gray images of cyclic codes overF2+uF2+vF2is a 3-quasi-cyclic code overF2.We believe that some better codes can be obtained as the images of cyclic codes over the ringF2+uF2+vF2.
Another direction for research in this topic is of the generalizationFq+uFq+vFqof F2+uF2+vF2,where q is a prime power.
[1]BONNECUZE A,UDAYA P.Cyclic codes and self-dual codes overF2+uF2[J].IEEE Trans Inform Theory, 1999,45(4):1250-1255.
[2]YILDIZ B,KARADENNIZ S.Cyclic code overF2+uF2+vF2+uvF2[J].Des Codes Crypt,2010,58: 273-287.
[3]HAMMANS A R,KUMAR P V,CALDERBANK A R,et al.Theℤ4linearity of Kerdock,Preparata, Goethals and related codes[J].IEEE Trans Inform Theory,1994,40:301-319.
[4]ZHU Shi-xin,WANG Yang,SHI Min-jia.Some results on cyclic codes overF2+vF2[J].IEEE Trans Inform Theory,2010,56(4):1680-1684.
[5]ABUALRUB T,SIAP I.Cyclic codes over the ringsℤ2+uℤ2andℤ2+uℤ2+u2ℤ2[J].Des Codes Crypt, 2007,42:273-287.
[6]WOLFMANN J.Nagacylic and cyclic codes overℤ4[J].IEEE Trans Inform Theory,1999,45(7):2527-2532.
[7]WOLFMANN J.Binary image of cyclic codes overℤ4[J].IEEE Trans Inform Theory,2001,47(5):1773-1779.
[8]WOOD J.Duality for modules over f i nite rings and applications to coding theory[J].Amer J Math,1999, 121:555-575.
[9]TAPIA-RECILLAS H,VEGA G.Some constacylic codes overℤ4and binary quasi-cyclic codes[J].Discrete Applied Math,2003,128:305-316.
[10]HUFFMAN W C,PLESS V S.Fundamentals of Error-correcting Codes[M].Cambridge:Cambrige University Press,2003.
tion:94B05,13A99
CLC number:O157.4Document code:A
1002–0462(2014)02–0189–06
date:2012-05-21
Supported bytheScientif i cResearchFoundationofEducationDepartmentof Hubei Province(B2013069);Supported by the National Science Foundation of Hubei Polytechnic University of China (12xjz14A,11yjz37B)
Biography:LIU Xiu-sheng(1960-),male,native of Huangshi,Hubei,a professor of Hubei Polytechnic University,engages in algebra coding.
 Chinese Quarterly Journal of Mathematics2014年2期
Chinese Quarterly Journal of Mathematics2014年2期
- Chinese Quarterly Journal of Mathematics的其它文章
- Group Twisted Tensor Biproducts over Hopf Group Coalgebras
- A Class of Solvable Lie Algebras and Their Hom-Lie Algebra Structures
- Positive Solutions for Fourth-order Delay Dif f erential Equation of Boundary Value Problem with p-Laplacian
- A New Nonlinear Integrable Couplings of Yang Equations Hierarchy and Its Hamiltonian Structure
- The Existence and Uniqueness of the Solution for Periodical Boundary Value Problems of 2kth Order Dif f erential Equations with Resonance
- On the Characterization of Cyclic Codes over RingF2+uF2+vF2
