主动自导回波信号的非线性偏离特性

申 珅，程 宏，王明洲

(1.中国船舶重工集团公司 第705研究所,陕西 西安 710075;2.中国船舶重工集团 第750试验场，云南 昆明 650051；3.水下信息与控制重点实验室,陕西 西安 710075)

主动自导回波信号的非线性偏离特性

申 珅1,3，程 宏2，王明洲1，3

(1.中国船舶重工集团公司 第705研究所,陕西 西安 710075;2.中国船舶重工集团 第750试验场，云南 昆明 650051；3.水下信息与控制重点实验室,陕西 西安 710075)

基于非线性动力学原理，主要研究正弦信号、主动自导回波信号以及经滤波归一化处理后的自导回波信号的相轨迹运动特性，并对经滤波归一化处理后的自导回波信号和正弦信号从偏离性方面进行比较分析。结果表明，主动自导回波信号的相轨迹运动特性及偏离特性的可分性显著。

主动自导回波信号；非线性；相轨迹；偏差

0 引 言

非线性是一种普遍存在于自然界和工程应用中的现象，但是由于非线性现象的复杂性，目前还没有找到一种统一的、普遍适用的描述方法来对其进行分析和处理。对于非线性系统，随机性激励只能引起随机性响应，而确定性激励不仅能引起确定性响应，也可以引起随机性响应(即混沌现象)。

水下目标信号的特征提取是水中兵器研究的重要内容。传统的目标信号特征提取方法主要有时域的相关函数法和频域的功率谱法。近年来,随着非线性动力学理论的发展，人们发现一些通常被认为是随机的、非平稳的信号具有非线性特性，水声信号便是其中之一。由于非线性动力学理论具有对非高斯、非平稳信号进行有效处理的能力,因此,用它对水下目标信号进行处理,显示了一定的优越性。本文主要讨论了正弦信号、经滤波后的主动自导回波信号和经滤波归一化后的回波信号的相轨迹运动特性，计算了经滤波归一化后回波信号与正弦信号的偏差。经分析发现主动自导回波信号具有非线性特性，并且这些非线性特性具有一定的可分性。这一结果对于水下目标信号的识别具有一定的参考价值。

1 正弦信号的相轨迹特性

正弦信号是频率成分最为单一的一种信号。任何复杂信号都可以通过傅离叶变换分解为许多频率不同、幅度不等的正弦信号的迭加。正弦信号可表示为：

x(t)=Asin(2πf0t+φ)，

(1)

式中：A为振幅；f0为信号频率；φ为初相角。

本文主要研究正弦信号的非线性特性，令

x′(t)=x(t+1)-x(t)，

(2)

研究(x,x′)的相平面轨迹运动特性。固定φ值，令f0在18～22kHz内变化。经仿真可知正弦信号的相轨迹运动均相似，(x,x′)的相轨迹呈椭圆形。图1是固定值φ=45°时，正弦曲线的相轨迹运动图，其相轨迹亦呈椭圆形。

图1 正弦信号的相轨迹图Fig.1 The phase track of the sinusoidal signal

2 主动自导回波信号的相轨迹特性

样本数据为实测的主动自导回波信号，该主动自导回波信号中包括混响、环境噪声及目标回波信号等。已知自导系统的发射信号是矩形波，信号脉宽为24ms，数据为复数形式，共采集10个周期的主动自导回波信号数据。

在实测数据处理中选取4个周期的数据样本。对实测的原始数据进行滤波处理，只保留目标回波信号，然后对各周期进行滑动窗FFT变换处理，确定是否包含目标回波信号。根据自导发射信号的脉宽，可确定FFT变换滑动窗长度为480，将各周期数据按480个点为1组，每次滑动1/4个窗长度算作下1组，从而将整个周期数据样本分成若干个小组。分别从各周期中随机选取3组不含目标回波信号和3组包含目标回波信号的数据，观察各组数据的相轨迹运动规律，图2是第1周期实测信号经滤波处理后的6组数据相轨迹图。

由图2可看出，包含目标回波信号段的(72组、73组、74组)与不包含目标回波信号段的(22组、41组、61组)其相轨迹全完不同，具有可分性。

图2 第1周期信号滤波后的相轨迹图Fig.2 The phase track of the first period signal after filtering

包含目标回波信号段的其相轨迹类似于正弦信号的相轨迹，呈椭圆形绕动。而不包含目标回波信号段的其相轨迹随机的在坐标原点附近绕动，无规律可寻。由此可知主动自导回波信号的相轨迹运动特性具有显著的可分性。

3 主动自导回波信号的偏离特性

由图1和图2可知，经滤波处理后的主动自导回波信号其含目标回波信号段的相轨迹运动呈规律的椭圆形，类似于正弦信号的相轨迹运动规律。为更好辨别出目标回波信号段，对滤波后的主动自导回波信号作进一步处理，将其相轨迹与正弦信号的相轨迹作比较，再观察它们的相轨迹运动规律。

由基本数学公式知，对所有复数x,有

sin2(x)+cos2(x)=1，

(3)

sin′x=cosx，

(4)

由式(3)和式(4)有

sin2x+(sin′x)2=1，

(5)

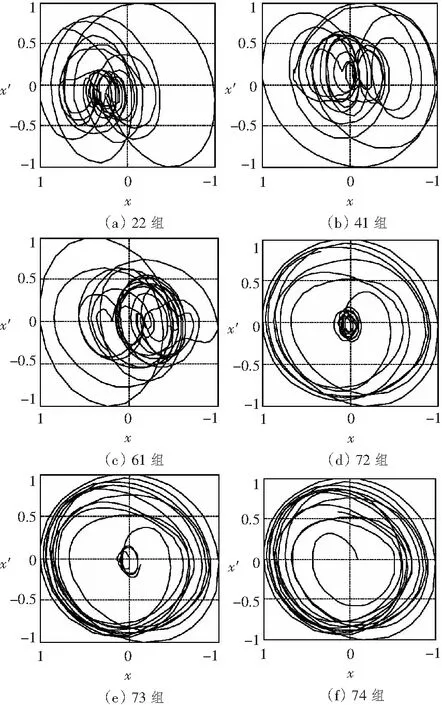
图3 第1周期信号滤波归一化后的相轨迹图Fig.3 The phase track of the first period signal after filtering and normalizing

所以定义偏差ε为

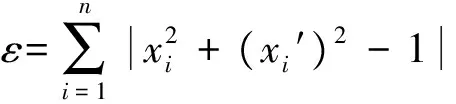
(6)

因此，将各周期主动自导回波信号经滤波处理后产生的新数据归一化在-1～1之间，再按上述步骤处理新数据，观察其相轨迹运动变化的规律并计算其偏差ε。图3是第1周期原始数据经滤波、归一化处理后的6组数据相轨迹图。表1是对第1周期信号进行滤波、归一化处理后的分析结果。

从图6和表1中可看出，包含目标回波信号段的其相轨迹呈圆周运动，且偏差较小，并且随着数据段中目标回波信号信息量的增加偏差越来越小。而不包含目标回波信号段的其相轨迹随机的在相平面内运动，无规律可寻，且偏差较大。

表1 第1周期信号滤波归一化后特性

4 结 语

水下主动自导回波信号的非线性特征量提取是水中兵器中鱼雷制导与水雷引信研究的一个新的内容,它弥补了传统的利用时域和频域方法对水下目标回波信号进行特征提取时存在的局限性。本文首先通过对正弦信号和经滤波处理后的自导回波信号的相轨迹作比较，得出了其相轨迹运动的相似性。然后进一步对实测自导回波信号数据作滤波归一化处理，通过计算其与正弦信号的偏差，得出了自导回波信号的偏离特性。本文主要从非线性动力学的角度更加有效地描述了水下自导回波信号的特征,为水下目标回波信号的特征识别寻找一种新方法。

[1] 黄永念.非线性动力学引论[M].北京大学出版社，2010.

[2]DANIELK,LEONG.Understandingnonlineardynamics[M].SpringerVerlag,1997.

[3] 李志舜.鱼雷自导信号与信息处理[M].西北工业大学出版社，2004.

[4] 周德善，李志舜，朱邦元.鱼雷自导技术[M].国防工业出版社，2009.

[5] 张德丰.MATLAB通信工程仿真[M].北京：机械工业出版社，2010.

[6] 李辉.混沌数字通信[M].北京：清华大学出版社，2006.

[7] 聂春燕.混沌系统与弱信号检测[M].清华大学出版社，2009.

Nonlinear departure feature of active homing echo signal

SHEN Shen1,3, CHENG Hong2, WANG Ming-zhou1,3

(1.The 705 Research Institute of CSIC,Xi′an 710075,China; 2.The 705 Proving Ground of CSIC,Kunming 650051,China; 3.Science and Technology on Underwater Information and Control Laboratory,Xi′an 710075,China)

Based on the nonlinear dynamics theory, this thesis primarily researches the phase orbit motion characteristic of sinusoid signal.active homing echo signal and active homing echo signal after filtering and normalizing, and compares the active homing echo signal after filtering and normalizing with the sinusoid signal. The experimental results show that the phase orbit motion characteristic and the deviation feature of active homing echo signal have the significance separability.

active homing echo signal;nonlinear;phase orbit;deviation

2013-10-16；

2014-01-08

申珅(1989-)，女，硕士研究生，研究方向为水声工程。

TB56

A

1672-7649(2014)03-0077-03

10.3404/j.issn.1672-7649.2014.03.015