均匀带电圆环片的空间静电场分布

贾秀敏

（河北科技大学理学院，河北 石家庄 050018）

文献［1，2］采用电势叠加原理，文献［3］采用延拓法和方程法等，对均匀带电圆盘或圆环的电势进行了分析，但计算过程都很复杂.本文在柱坐标系中利用的柱函数展开式及贝塞尔函数的性质，很方便地得到了均匀带电圆环片在空间产生的电势及场强.

1 电势分布

研究的问题是：内外半径分别是a和b的圆环片，均匀带电且电荷面密度为σ，计算空间任意一点的静电场.建立如图1所示柱坐标系 （ρ，φ，z），在环 片 上 P′（ρ′，φ′，z′）处 取 电 荷 元 dq′ ＝σdS′＝σρ′dρ′dφ′，此电荷元在空间任意点P（ρ，φ，z）处产生的电势元为

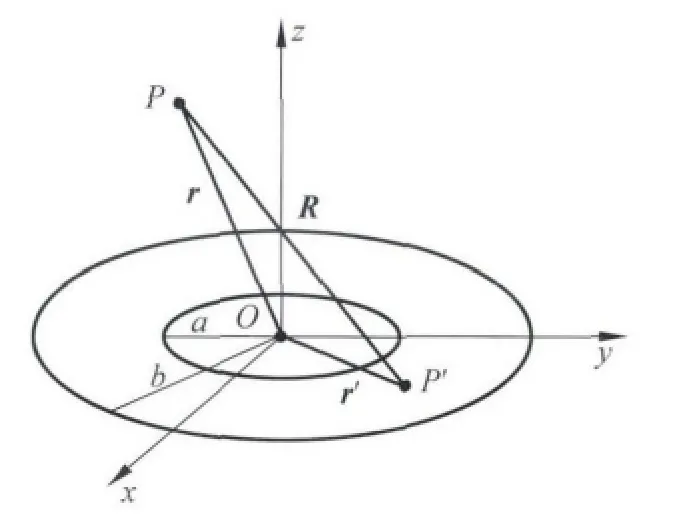
图1 均匀带电圆环片

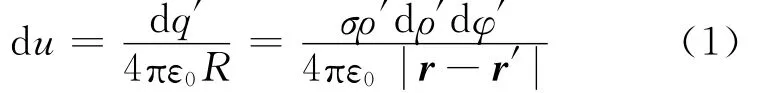
其中，r、r′分别为P点和P′点的位置矢量，R＝r－r′.

在柱坐标系中，源点到场点的距离 r－r′的倒数的柱函数展开式［4］为

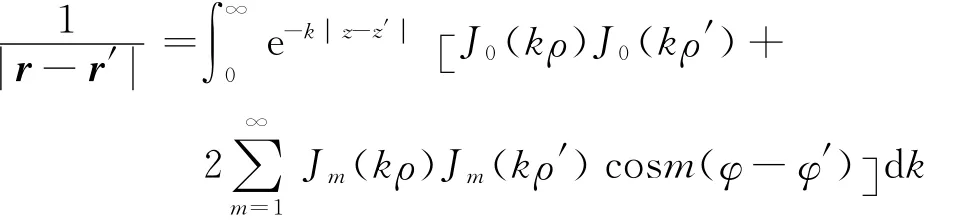
由于圆环片在xOy面上，即z′＝0；由电荷分布的对称性可知，电势与方位角φ无关，可令φ＝0，将式（1）叠加得到整个圆环片在场点P产生的电势为

由三角函数的正交性知

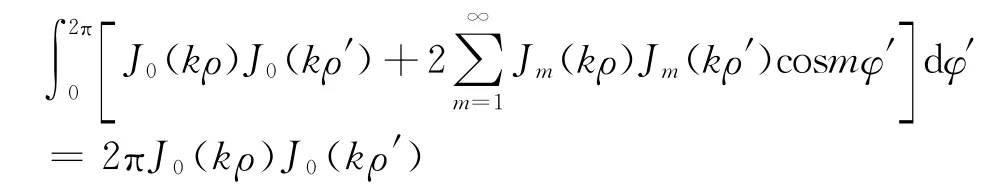
应用公 式［5］［xJ1（x）］′＝xJ0（x），则 圆 环 片 在P（ρ，φ，z）处产生的电势为

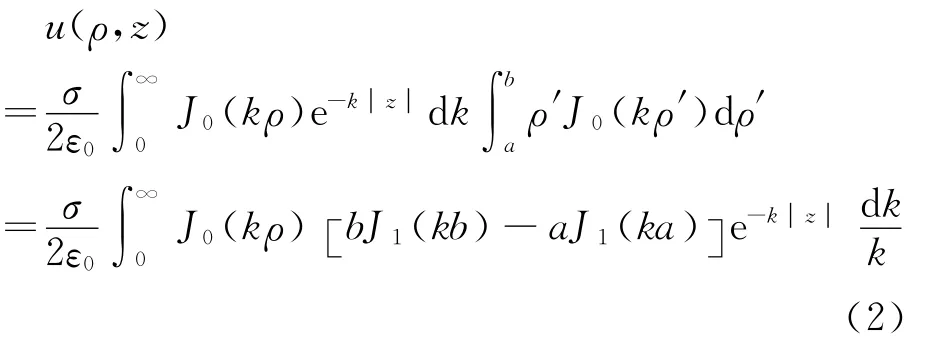
2 场强分布

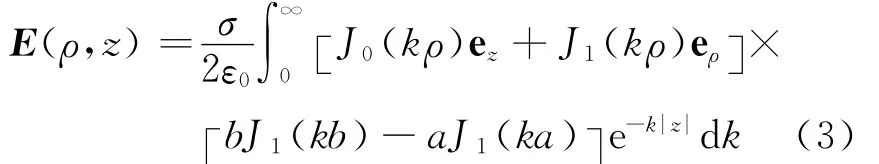
3 讨论

（1）a＝0时，由式（3）得带电圆盘在空间产生的场强

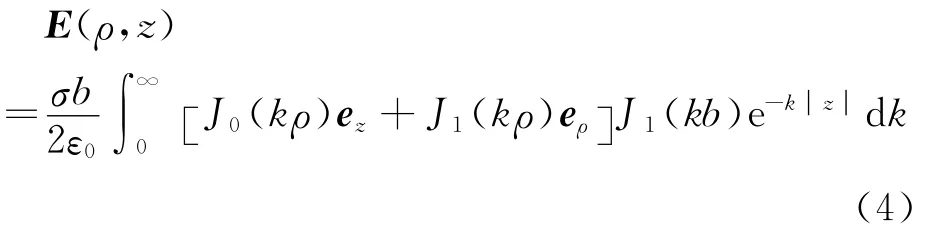
当ρ→0时，J1（kρ）＝0；J0（kρ）＝1，应用公式［5］，由式（4）得带电圆盘轴线上的场强为

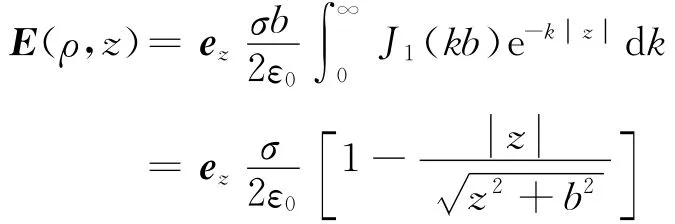
与文献［6］结果相同.

（2）b→∞时，则所研究场点可视为在轴线附近，J0（kρ）、J1（kρ）可以取小宗量渐近表达式［7］，并利用公式［5］

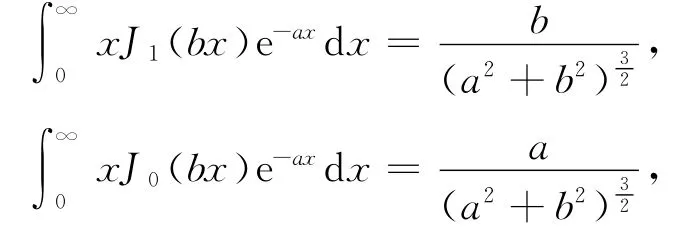
由式（3）可得挖去半径为a的圆孔后的无限大带电薄板在空间产生的场强

可见，当所研究的问题具有轴对称性时，利用柱函数展开式能更方便地分析其形成的空间静电场，其求法对柱体、螺线管等形成的电磁场同样适用.

［1］ 历爱皊，姜黎霞.均匀带电圆盘电位的空间分布［J］.山东农业大学学报，2003，34（04）：559－561.

［2］ 侯昭武.均匀带电宽圆环空间静电势［J］.广西右江民族师专学报，2004，17（06）：25－28.

［3］ 吴崇试.均匀带电圆盘的静电势问题［J］.大学物理，2000，19（11）：1－4.

［4］ 杰克逊JD.经典电动力学（上）［M］.朱培豫，译.北京：人民教育出版社，1978：131，146.

［5］ 刘式适，刘式达.特殊函数［M］.北京：气象出版社，2002：406，410，408.

［6］ 马文蔚.物理学［M］.北京：高等教育出版社，2006：160.

［7］ 《数学手册》编写组.数学手册［M］.北京：人民教育出版社，1979：630.