方中空夹层钢管混凝土压扭构件承载力计算方法研究

郭立湘，李 婷，杨 建，黄 宏

(1.江西杭萧钢构有限公司，江西 南昌 330013;2.华东交通大学土木建筑学院，江西南昌 330013;3.青岛理工大学(临沂)土建工程系，山东临沂 273400)

上世纪90年代后，一种将混凝土浇注在两根同心放置的钢管之间的组合结构——中空夹层钢管混凝土以其特有的优点被广泛运用于实际工程当中;当高耸结构、厂房柱、送变电杆塔等受压构件在地震荷载作用下，构件将同时受到压力和扭矩的共同作用[1-2]。采用有限元法可以较为精确地计算中空夹层钢管混凝土压扭构件承载力，但是计算过程繁杂，耗费时间较长，不适合推广至工程实践当中，因此有必要提出压扭构件承载力简化计算方法。本文将针对外钢管截面为方形，内钢管截面为圆形的方中空夹层钢管混凝土压扭构件承载力简化计算方法进行研究。

国内外已有较多学者对钢管混凝土扭转、压扭等构件承载力计算的研究报道。韩林海等[3-4]提出了钢管混凝土压扭、弯扭构件的承载力简化计算方程及纯扭构件承载力简化计算公式。金伟良等[5]提出了薄壁离心钢管混凝土纯扭构件扭矩—转角全过程曲线三阶段的承载力简化计算方法。袁伟斌等[6]提出了离心钢管混凝土弯扭构件承载力相关方程。王宇航等[7]基于“分层筒”理论，提出了钢管混凝土纯扭构件的承载力简化计算公式、压扭构件承载力相关方程。对于中空夹层钢管混凝土扭转构件承载力简化计算的研究已有报道[8]，而对于中空夹层钢管混凝土压扭构件承载力简化计算方法的研究尚无报道。

本文在有限元计算结果得到既有试验结果验证的基础上，通过有限元法分析外钢管强度、内钢管强度、混凝土强度、空心率、内管径厚比、名义含钢率、长细比各参数对方中空夹层钢管混凝土压扭构件T/Tu－N/Nu相关曲线的影响。在此基础上，提出压扭构件承载力相关方程，并将简化计算值与有限元计算值、试验值进行比较分析，以验证简化计算方程的可靠性。

1 试验简介

本课题组以长细比、空心率和轴压比为变化参数，对6根方中空夹层钢管混凝土和1根方钢管混凝土构件进行了压扭试验研究，试件参数见表1。表中L为试件长度，Bo和to分别为外钢管的边长和管壁厚度，Di和ti分别为内钢管的直径和管壁厚度，fyo和fyi分别为外钢管和内钢管的屈服强度，fcu为混凝土的立方体抗压强度，λ为长细比(λ=L/i，i为截面回转半径)，χ为空心率(χ=Di/(Bo－2to))，n为轴压比(n=N/Nu，N为试件所受轴力，Nu为轴心受压强度承载力)，Tue为抗扭强度承载力试验值，Tuc1为抗扭承载力有限元计算值，Tuc2为抗扭承载力简化计算值。采用有限元法对试件进行分析计算(有限元建模方法同文献[9])，将有限元计算结果与试验所测得的扭矩—转角曲线进行比较，可得有限元计算曲线与试验所测得曲线吻合，通过计算可得Tuc1/Tue的平均值为0.960，均方差0.072，可知试件抗扭承载力的有限元计算值与试验值吻合良好。图1给出了试件SDL-4，SL-4的有限元计算与试验所测得的扭矩—转角关系曲线，实线为有限元计算所得曲线，虚线为试验所测得曲线[10]。

表1 试件参数一览表

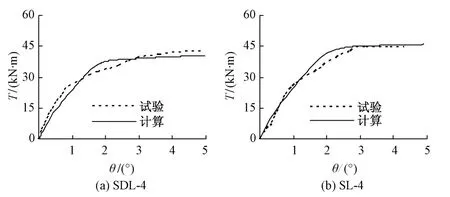
图1 有限元计算曲线与试验所测得曲线的比较

2 各参数对T/Tu－N/Nu相关曲线的影响

在有限元计算结果得到既有试验结果验证的基础上，采用文献[9]中的建模方法分析方中空夹层钢管混凝土典型压扭构件外钢管强度、内钢管强度、混凝土强度、空心率、内管径厚比)、名 义含钢率Aso/Ace，Aso为外钢管截面面积，Ace表示外钢管截面内部包含的空隙面积，Ace=(Bo－2to))2和长细比参数变化时对构件T/Tu－N/Nu相关曲线的影响，如图2所示。由该图可知，长细比变化时对方中空夹层钢管混凝土压扭构件T/Tu－N/Nu相关曲线的影响较明显，其他参数变化对T/Tu－N/Nu相关曲线的影响不显著，故在推导T/Tu－N/Nu承载力相关方程时可略去参数外钢管强度、内钢管强度、混凝土强度、空心率、内管径厚比和含钢率的影响。分析时典型构件计算参数分别为:L=1 200 mm，Bo=400 mm，to=9.3 mm，Di=190.7 mm，ti=3.18 mm，fyo=345 MPa，fyi=345 MPa，fcu=60 MPa。

图2 各参数对构件T/Tu－N/Nu相关曲线的影响

3 承载力简化计算方程

采用有限元法可以较精确地计算方中空夹层钢管混凝土压扭构件承载力，但是数值计算过程繁杂，耗费的时间较长，不适合推广至工程实践当中，因此有必要提出压扭构件承载力相关方程。通过上述各参数对T/Tu－N/Nu相关曲线的影响并参考文献[11]中方钢管混凝土压扭构件承载力相关方程，方中空夹层钢管混凝土压扭构件承载力相关方程可以采用如下表达式

式中，Nu和Tu分别为方中空夹层钢管混凝土轴压强度承载力和纯扭构件的极限承载力，其中Tu由文献[8]中方中空夹层钢管混凝土纯扭构件抗扭承载力简化计算公式计算得出，表达式为

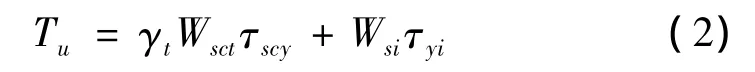
其中，γt为抗扭承载力修正系数，与空心率χ有关，Wsct为方钢管混凝土截面抗扭模量，其值按文献[4]中取为0.208B3

o(Bo为外钢管边长)，τscy为方中空夹层钢管混凝土抗扭屈服极限，Wsi为内钢管截面抗扭模量，τyi为内钢管抗扭屈服极限。式(2)中各参数表达式为

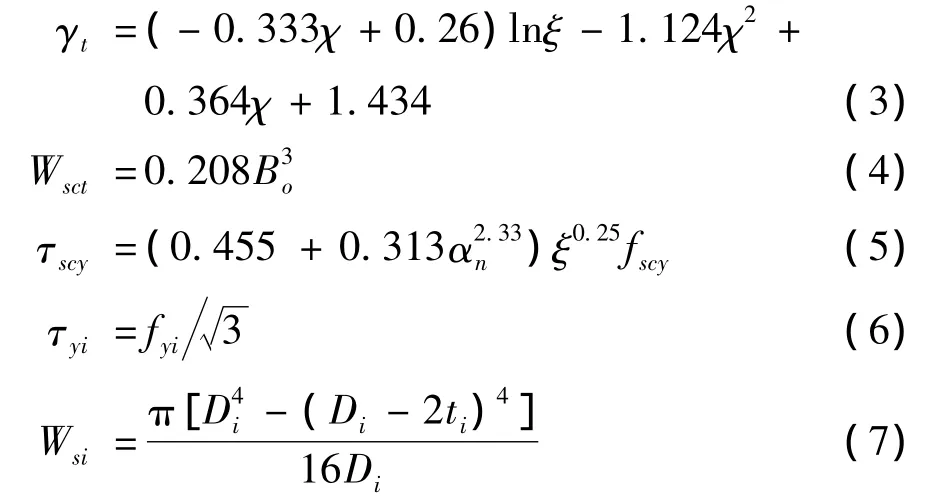
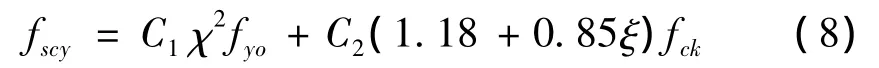
式中C1，C2为计算系数，C1=α(1+α)，C2=(1+αn)/(1+α)，α =Aso/Ac表示含钢率。

式(1)中Nu按下式确定[1]

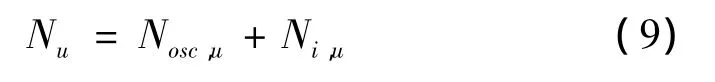
式中，Nosc，u为外钢管和混凝土的轴压极限承载力，Ni，u为内钢管的极限承载力(Ni，u=Asifyi)。Nosc，u的表达式为

式中，Asco=Aso+Ac，Aso为外钢管截面面积，Ac为混凝土截面面积，fscy为外钢管与夹层混凝土的组合抗压屈服极限，按式(8)计算。

考虑构件长细比λ的影响，压扭构件T/Tu－N/Nu相关曲线简化计算方程为

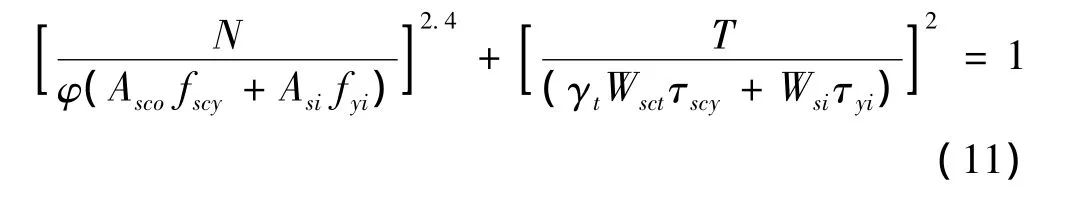
式中，φ为方中空夹层钢管混凝土轴压稳定系数，计算公式为

其中:

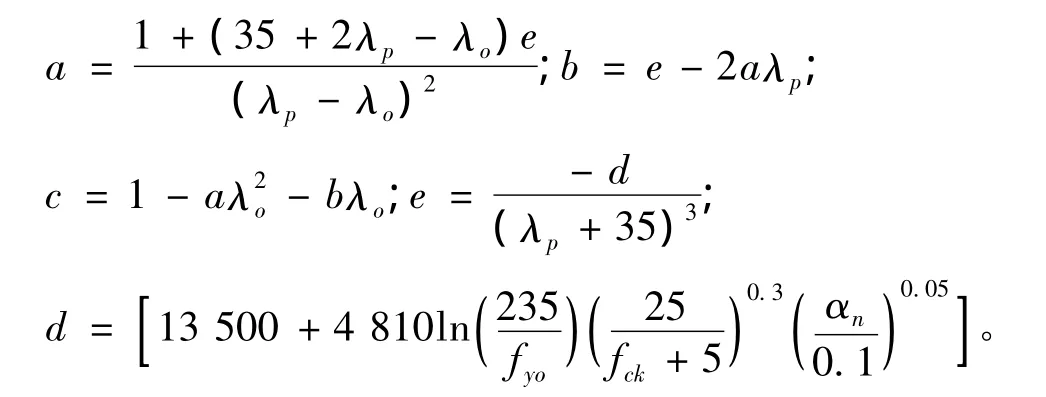
式中，λp，λo分别为方中空夹层钢管混凝土轴压构件发生弹性或弹塑性失稳时的界限长细比，计算公式为

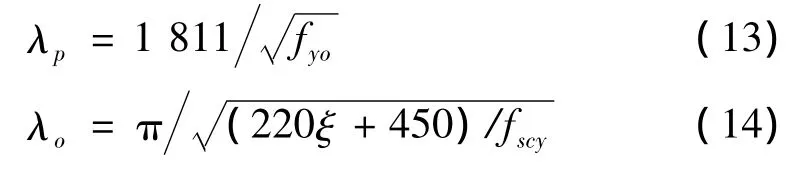
式中，fyo和fscy单位为 MPa。

4 简化计算值与有限元计算值、试验值比较

在上述参数影响范围内，即fyo=235～500 MPa，fyi=235～500 MPa，fcu=30～90 MPa，χ=0.25～0.75，Di/ti=30～90，αn=0.05～0.20，采用上述简化计算方程式(11)所得的计算值(Tuc2)与有限元计算值(Tuc1)进行了比较，如图3所示。通过计算可得，Tuc2/Tuc1的平均值为0.950，均方差为0.055，可知简化计算方程与有限元法计算的结果吻合良好。

图3 简化计算值与有限元计算值比较

采用简化计算方程式(11)对表1中方中空夹层钢管混凝土试件进行了承载力计算。图4列出了试件承载力简化计算值与试验值的比较，结合表1中数据可得，Tuc2/Tue的平均值和均方差分别为0.906和0.066，可知试件的简化计算值与试验值比较吻合而且均偏安全，为工程实际运用提供参考。

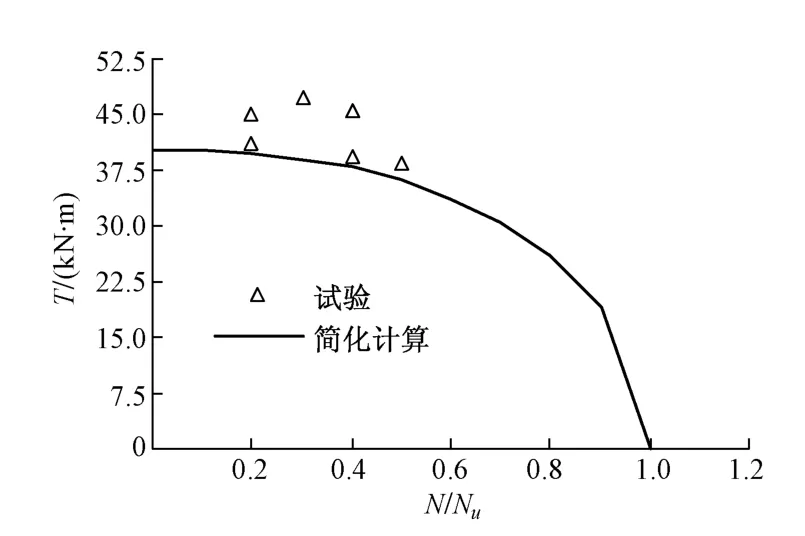
图4 试件简化计算值与试验值的比较

5 结论

1)在方中空夹层钢管混凝土压扭构件中，外(内)钢管强度、混凝土强度、空心率、内管径厚比、名义含钢率参数变化时对T/Tu－N/Nu相关曲线的影响不明显，长细比参数变化时对T/Tu－N/Nu相关曲线的影响较显著。

2)提出了方中空夹层钢管混凝土压扭构件承载力简化计算方程，简化计算值与有限元计算值、试验值吻合良好，可以供工程设计参考。

[1]陶忠，于清.新型组合结构柱——试验、理论与方法[M].北京:科学出版社，2006.

[2]黄宏，黄诚，陈梦成.方中空夹层钢管混凝土压弯构件滞回性能的有限元分析[J].铁道建筑，2010(7):57-61.

[3]韩林海，钟善桐.钢管混凝土压扭、弯扭构件承载力相关方程[J].哈尔滨建筑工程学院学报，1994，27(2):35-37.

[4]HAN L H，YAO G H，TAO Z.Performance of concrete-filled thin-walled steel tubes under pure torsion[J].Thin-Walled Structures，2007，77(1):24-36.

[5]金伟良，曲晨，傅军，等.薄壁离心钢管混凝土扭转全过程简化计算研究[J].浙江大学学报:工学版，2003，37(1):5-9.

[6]袁伟斌，金伟良.离心钢管混凝土弯扭构件试验研究与理论分析[J].浙江大学学报:工学版，2008，42(1):116-121.

[7]WANG Yuhang，NIE Jianguo，FAN Jiansheng.Theoretical model and investigation of concrete filled steel tube columns under axial force-torsion combined action[J].Thin-Walled Structures，2013，83(8):1-9.

[8]HUANG Hong，HAN Linhai，ZHAO Xiaolin.Investigation on concrete filled double skin steel tubes(CFDST)under pure torsion[J].Journal of Constructional Steel Research，2013，90(9):221-234.

[9]黄宏，郭晓宇，陈梦成.圆中空夹层钢管混凝土压扭构件有限元研究[J].建筑结构学报，2013，34(增1):332-338.

[10]杨建.方中空夹层钢管混凝土柱在压扭受力下的研究[D].南昌:华东交通大学，2012.

[11]韩林海.钢管混凝土结构——理论与实践[M].北京:科学出版社，2007.