基于动力学特征的疏散时间预测模型及其在高校的应用

杨程炜， 郑小敏， 刘宇轩， 黄文冰

(华南师范大学 数学系, 广东 广州 510631)

基于动力学特征的疏散时间预测模型及其在高校的应用

杨程炜， 郑小敏， 刘宇轩， 黄文冰

(华南师范大学 数学系, 广东 广州 510631)

运用文献资料法、模拟实验法、走访调查法等研究方法，建立了基于动力学特征的人群疏散时间的预测模型.引入楼梯距离与平地距离的折算思想，将局限于单层建筑的研究推广至多楼层的预测问题.走访多所高校教学楼，对其建筑特征进行总结，建立了适用于大多数高校教学楼的基于微分方程组的疏散时间预测模型.

高层建筑；疏散模型；动力学特征；微分方程组；预测

0 引言

部分校园的配套设施存在不同程度的电力设备线路老化、用电负荷较高等问题，这些问题增加火灾事故发生的可能.另外，地震等突发事件一旦发生，将会使师生们的生命安全遭受严重威胁，事先的疏散时间预测能够给校方提前改善疏散环境提供有效的依据.在人群疏散的研究领域中，一般认为，人员应急疏散模型基本上可分成宏观和微观两类：宏观模型指仅考虑个体疏散运动的模型，将疏散个体“同质化”；微观模型是指综合考虑个体疏散运动与疏散行为之间关系的模型.近年来国内的相关研究取得一定的成果，但大多数学者停留在疏散模型自身的研究上，研究成果更多的是零散的疏散规律，少有考虑实际应用的需要，其中比较明显的体现就是大部分的微观模型局限于平面结构下进行.针对上述问题，笔者在吸纳了多种模型后，抽象出高校建筑的主要特征，将不同的模型进行了一定的组合，并首次将局限于单层建筑的研究推广至多楼层的应用当中,最终得出一个适用于大多数高校的基于动力学特征的人群疏散时间预测模型.

1 研究对象与方法

1.1 研究对象

华南师范大学教学楼(本部和大学城校区)、广东工业大学教学楼(大学城校区)、华南农业大学教学楼(五山校区)、华南理工大学(大学城校区).

1.2 研究方法

1)文献资料法.通过检索中国知网、中国优秀硕博士论文文库等，收集与课题相关的文献资料.

2)模拟实验法.根据研究的需要，设计模拟实验测定实际参数的值.

3)走访调查法.走访、观察多座高校教学楼的结构，从而对高校建筑疏散结构进行抽象总结，并在华南师范大学、华南农业大学现场调查大学生的肩宽作为参数参考值.

4)数学建模法.用数学模型的思想研究疏散问题，利用数学中微分方程组思想对疏散过程进行模拟.

2 疏散模型的建立

2.1 前向距离—疏散速度函数

1)疏散的动力学特征研究.在疏散过程中，随着密度的增大,人员的运动速度逐渐降低,这是人员运动的基本规律,已经被众多学者通过实验进行了验证.文献[1]中定义的行人前向距离d，表示个体与前面相邻行人的间距,并在单列行人运动实验与模拟中发现，行人运动速度和前向距离d密切相关.采用基于mean-shift算法的行人分割与跟踪技术，分析计算其每一时刻的速度及前向距离,并最终得到结论：“在达到最大运动速度之前,随着前向距离增加,人员的运动速度呈近似线性增长.”

2)前向距离—疏散速度函数的参数确定.根据文献[2]给出的参数：亚洲人的平均体厚为0.32 m，行走不受约束的最小前向距离为1.12 m,而人员疏散的最大速度为1.36 m/s.将人视作质点，当人的前向距离等于0.32 m，则与前面的人紧挨着，因此速度为0.当人的前向距离为1.44 m，(即1.12 m加上体厚0.32 m)，人的速度刚好达到最大速度.当前向距离在0.32 m与1.44 m之间，则近似线性增长.因此，

(1)

其中，d指前向距离，函数指前向距离—疏散速度函数.

2.2 平地距离对楼梯距离的转换系数

人员的疏散包括楼梯部分以及衔接两段楼梯之间的平地，而“前向距离—疏散速度”是在平地距离的基础上，平地距离的定义与楼梯距离并不等价.因此，取楼梯的斜面距离作为研究，并引入转换系数用于将平地距离折算成等价的楼梯斜面距离.所谓的“等价”，就是指人在相同的运动状态下、在相同的紧张程度等作用下，在相同时间内完成的在平地位移与楼梯斜面位移等价.而等价的楼梯斜面距离与平地距离的比值即为转换系数.下面通过设计模拟实验进行测定(如图1和图2).

实验1 从m层楼梯的第一格楼梯开始，直到下一层楼梯的最后一格楼梯为止，记录时间为T.多次实验, 求出平均时间.

实验2 从m+1层通往m层楼梯的最后一格开始，(终点在实验1的基础上增加了一个平地的位移，如图1中A点为实验2的终点，B点为实验1的终点)测试从起点C到终点B和终点A少走的楼梯格数n.通过多次实验，求出n的平均值，并折算斜面距离，从而这两段距离等价.

经多次实验后，得到的参考值为0.375.

图1 模拟实验起点Fig.1 Starting point of simulation experiment

2.3 高校教学楼的楼层结构抽象及疏散特征总结

1)楼层结构抽象.走访了华南师范大学(本部和大学城校区)、广东工业大学(大学城校区)、 华南农业大学(五山校区)、广东外语外贸大学的各个教学楼，大多数的疏散楼梯结构可以抽象为单人流方向型、双人流汇聚型和平台型3类(图3～图5).

2)基于高校的建筑结构与疏散特征的合理假设.基于高校建筑的3种抽象结构以及人员密集的特点，可有以下5个假设.

①在紧急事件发生后，各楼层人员的响应时间相等 (可视作高校的火灾警报系统或广播系统的通知)；

②每层楼的人员最终形成有序队伍，且同一楼层疏散队伍不出现断裂现象；

③人员在经过狭窄的建筑节点、汇聚楼梯口时自动形成队伍，人员密集保证队伍不断裂；

④楼梯的选择遵循“就近原则”；

⑤疏散过程中，不同楼层队伍遵循“先后原则”.

图3 单人流方向型Fig.3 Single direction type

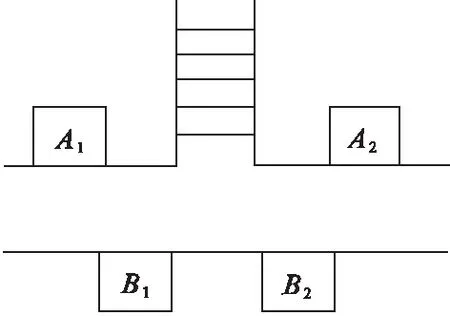
图4 双人流汇聚型Fig.4 Double direction type

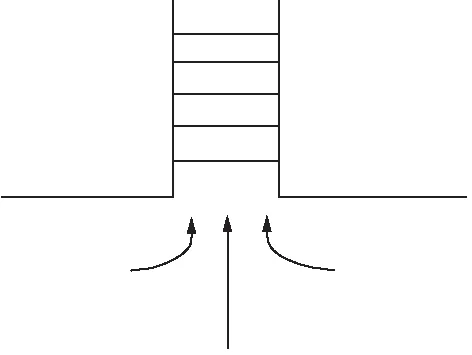
图5 平台型Fig.5 Multidirection type

2.4 疏散过程建模

2.4.1 部分符号说明

i为队伍每一行各自的编号，不同楼层自下而上累加i=1,2,…,n(图2)；第i行人员的疏散路程Si(t)、速度vi(t)、前向距离关于时间的函数di(t)；一格楼梯的斜面距离d0(人与人在楼梯上前向距离的初始值)；第j层队伍首行所在的编号ij，j=1,2,…,m，共m层楼；第j层队伍的长度Lj，j=1,2,…,m；楼层j从教室到楼梯的最短距离S1j，j=1,2,…,m；一段楼梯的斜面长度Slt(图1)；连接两段楼梯的平地的弧形距离Shu(图1)；从最高楼层(m层)疏散到地面的总路程Ssum;平地距离对楼梯距离的转换系数c1;最大疏散速度Vmax.

2.4.2 疏散过程

1)响应阶段T0，即火灾警报拉响后到学生从教室撤离在教室外列队整齐后的时间段.

2)全速撤离阶段.各层人员以最大速度(无障碍)从距离楼梯最近的教室门口走到下一层楼梯的时间为T1,其中路段包括从教室到楼梯的最短距离、两段楼梯以及两段连接楼梯之间的弧形长度，

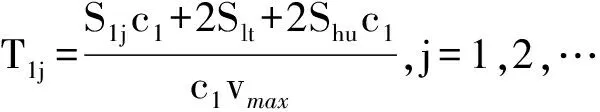
(2)

3)模拟阶段.

对于任意t时刻，第i行队伍的疏散速度：

(3)

对于任意t时刻,第i行队伍的前向距离：

①若第i行与第i-1行来自同一楼层,

di(t)=Si-1(t)-Si(t)+d0=g(Si,Si),i=1,2,…,n;

(4)

②若第i行是第j层队伍的首行(第i-1行是第j-1层的末行),

di(t)=Si-1(t)-Si(t)+2Slt+2Shuc1-Lj-1=h(Si,Si,Lj-1).

(5)

所以，得到如下微分方程组模型:

①当i∉{i1,i2,…,im}时，

(6)

②当i=ij时，

(7)

注 函数f(·)指前向距离—疏散速度函数.

4)初始条件.

①Lj由给定的各层疏散人数及楼梯宽度决定;

(8)

5)模拟结束条件，

Sn(t)=Ssum(n指最后一行队伍).

(9)

6)求解结果，模拟结束时的t即为求解的疏散总时间.

2.4.3 其他参数的计算公式

S0为楼梯的宽度，Nj为第j层疏散的人数，n0为楼梯能容纳的队伍列数，d邻为疏散时人与人左右相隔距离.

1) 平均肩宽参考值为0.38 m(问卷调查的结果)， 测量参考值为0.15 m；

(10)

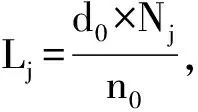
4)对于m层建筑，Ssum(m)=c1S1m+m×(2Slt+2Sltc1).

图6 列数与宽度的关系Fig.6 Relation of column and width

2.4.4 模型的应用方法

本模型用于求解一条楼梯的疏散时间，而对于多疏散通道的教学楼，则只要收集教学楼的排课信息，按照“就近原则”，对每条疏散楼梯划分大致的管辖区域，即可得出楼梯每层疏散人数.另外，再测量S0,Shu,Slt,S1j(j=1,2,…,m)，即可利用上述模型求解各条楼梯的疏散时间，以最长的时间作为整栋教学楼的疏散总时间即可.

3 结语

疏散模型基于高校建筑典型特点、高校人员疏散特征作出假设，合理地模拟疏散过程，从而使模型针对性强，具有实际应用价值.但值得注意的是，上述模型并不一定能适用于所有高校，因此在使用前应判断能否较好地满足2.3节2)中的5个假设.

[1] 房志明.考虑火灾影响的人员疏散过程模型与实验研究[D].安徽:中国科学技术大学,2012:33-38.

[2] 王振,刘茂.人群疏散的动力学特征及疏散通道堵塞的恢复[J].自然科学进展,2008,18(2):180-183.

A Forecast Model for Evacuation Basedon Kinetics Features and Its Application in Colleges

YANG Cheng-wei， ZHENG Xiao-min， LIU Yu-xuan， HUANG Wen-bing

(SchoolofMathematicalSciences,SouthChinaNormalUniversity,Guangzhou510631,China)

By documentary analysis, experiment simulation method, investigation and other methods, a forecasting model of crowd dispersal based on the characteristics of dynamics was set up. Commuting methods in converting stairs base length to diagonal distance was proposed so as to apply the limited laws of single-storey building to the prediction of multi-storey ones. Second, the shared features of different architectures had been summarized to set up a universally applicable model for crowd evacuation based on the differential equations.

multi-storey buildings; model for crowd evacuation; characteristics of dynamics; system of differential equations; forecast

2014-04-30

华南师范大学大学生创新创业训练计划“华南师范大学紧急通道疏散能力的量化评估”课题研究成果(1057413118)

杨程炜(1994—)，男，广东广州人，华南师范大学数学系.

10.3969/j.issn.1007-0834.2014.04.010

X913.4

A

1007-0834(2014)04-0038-04