基于小波包分解的含噪语音时频特性分析及端点检测

陈金龙 范影乐 倪红霞 武 薇

（杭州电子科技大学智能控制与机器人研究所，杭州，310018）

引 言

语音在采集传输以及通信过程中不可避免的会引入各种噪声，噪声的存在将降低语音的清晰度和可懂度。因此含噪语音输出质量的改善程度，将直接影响到后续语音识别［1-2］、语音编码［3］等算法的准确性和复杂度。目前语音处理方法主要包括短时傅立叶变换、小波分析和 Wigner-Ville分布等，上述方法考虑了语音信号在时频域上的特征表达，但他们仍基于语音信号具有短时线性平稳的假设，在语音的静态特征描述上具有较好的性能，但忽略了语音的非线性和非平稳特性。

1998年，Huang NE.［4］提出了一种适用于非线性、非平稳信号的Hilbert-Huang变换（Hilberthuang transform，HHT）时频分析方法。其在语音信号的时频特性分析中得到了广泛的应用。例如文献［5］将HHT方法应用于语音信号的周期估计，有效地提高了基音识别的准确性与分辨率。KI.Molla等人将Hilbert谱作为音频信号的时频描述，结果表明其与短时傅立叶变换相比具有显著的优势［6］。但在语音时频特性描述的上述应用中，HHT也暴露了存在模态混叠以及低频覆盖等局限性［7］。针对上述问题，本文在HHT基础上，利用小波包对语音信号进行分解以及对固有模态函数的自适应筛选，能够有效的将频带进行细分，避免模态混叠，改善含噪语音的时频分辨率；引入相关系数阈值准则对固有模态函数（Intrinsic mode function，IMF）分量进行筛选，避免 Hilbert谱中出现虚假频率。

1 基本原理

1.1 小波包分解

小波包分解（Wavelet package decomposition，WPD）具有良好的正交性、完备性、局部性，可将WPD视为函数空间中逐级正交剖分的扩展。WPD在所有的频率范围内聚集的特性，使其具有更好的局部时频滤波特性，适合对语音进行经验模态分解（Empirical mode decomposition，EMD）前的宽带细化。

正交小波包分解如式（1）

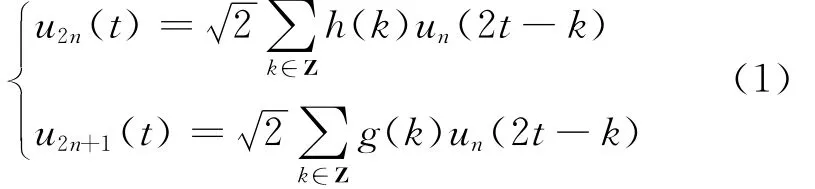
式中：g（k）＝（-1）kh（1-k），g（k）和h（1-k）是一对正交镜像滤波器。当n＝0时，u0（t）和u1（t）分别为尺度函数φ（t）和小波函数ψ（t）。

1.2 Hilbert-Huang变换

Hilbert-Huang变换包括两部分：EMD和Hilbert谱分析。

1.2.1 经验模态分解

EMD分解是把复杂的信号分解为有限个固有模态函数IMF分量之和，经过一系列分解后，信号x（t）被分解成n个固有模态函数ci（t）和一个余项rn（t），如式（2）所示

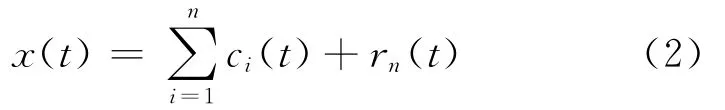
1.2.2 Hilbert谱

分解后得到的IMF分量通过Hilbert变换，求得瞬时频率，得到Hilbert谱。对每个固有模态分量ci（t）作 Hilbert变换

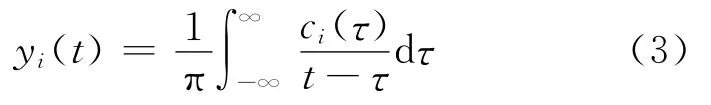
根据式（4）构造解析信号zi（t）

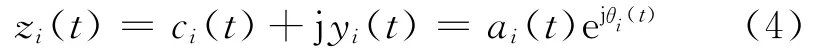
式中：ai（t）为解析信号幅值，θi（t）为相角

瞬时频率定义为

从而原始信号可以表示为

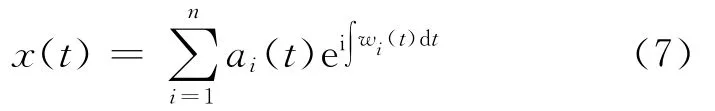
式（7）表明信号的幅值和瞬时频率都是时间的函数，从而可以在时频平面中将幅值表示成时间和瞬时频率的函数H（w，t），即原始信号的Hilbert谱。H（w，t）对时间积分，就得到Hilbert边际谱（Marginal spectrum，MS）

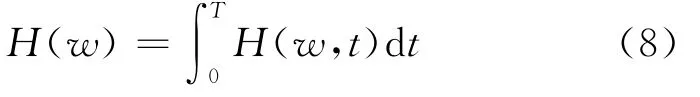
Hilbert瞬时能量谱（Instantaneous energy spectrum，IES）为H（w，t）对频率w的积分，其定义为

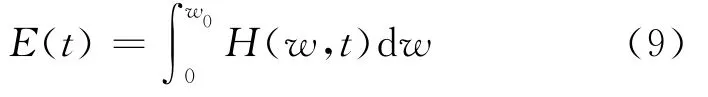
1.2.3 相关系数阈值准则IMF分量筛选

由于IMF分量和剩余信号rn（t）是原始信号的正交分量，因此相应的IMF与原信号具有很强的相关性。依次计算每个IMF与原信号的相关系数ri作为判别相关性的依据，表达式为

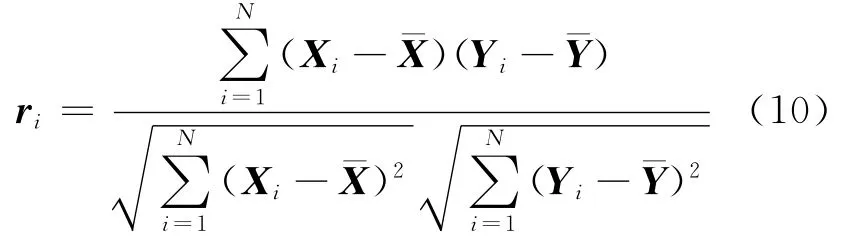
式中：i＝1，…，n，Xi为IMF分量序列，Yi为重构信号序列，N为采样点数，为Xi序列的均值，为Yi序列的均值。

对于n个IMF的相关系数ri（i＝1，…，n），剔除阈值为

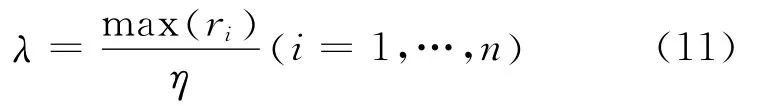
式中：η为比例因子。计算每个IMF的相关系数，筛选准则如下：若大于λ，则保留该IMF，否则剔除该IMF加入到剩余分量中。通过该方法，可以有效去除IMF中相关性较差的分量，避免希尔伯特谱中出现虚假频率分量［8］。

2 实验结果

本文实验数据为自采集数据库中的孤立词语：对象为50名来自全国各大区的大学生，每人读5次，每次读26个英文字母各一遍，采样频率为8kHz，16bit量化，wav格式。背景噪声数据来源于NOISEX92标准噪声数据库［9］，选择其中3种噪声，分别为飞机噪声（F16）、工厂噪声（Factory1）和办公室噪声（Babble）。对含噪语音均采用数字滤波器H（z）＝1-μz-1（μ＝0.937 5）进行预加重处理，用于消除低频交流电工频等干扰。

2.1 相关系数阈值准则的有效性

为了说明相关系数阈值准则的有效性，对含噪语音（工厂噪声，下同）用db3小波基进行3层分解，对分解的各个信号进行重构，得到重构信号，记为 WPDi（i＝1，2…，8），对重构信号进行 EMD分解，计算对应的IMF分量以及相关系数，结果如表1所示，其中η＝50。

从表1可以看出，EMD分解具有自适应性，表现为较高的相关系数一般集中于前几个EMD分解出来的IMF分量中。因此根据式（11）筛选出来的IMF分量在所有的IMF分量中占主导作用，也进一步说明相关系数阈值准则的有效性。通过相关系数阈值准则筛选有效的IMF分量，剔除相关系数较差的IMF分量，避免在Hilbert谱中出现虚假频率分量。

表1 各IMF与对应WPD分量的相关系数对比表Table 1 Correlation coefficient comparsion of each component of IMF and corresponding WPD

2.2 纯净语音和含噪语音的时频分析

基于小波包分解的HHT变换方法，采用相关系数阈值准则筛选IMF分量，分别对纯净语音和含噪语音进行Hilbert谱分析，如图1所示。图1（a，b）分别为纯净语音和含噪语音 WPD1的Hilbert谱，可以发现纯净语音在时间轴上2 000～5 000采样点之间有低频能量分布，而含噪语音在整个时间轴采样点上都存在低频能量分布。图1（c，d）显示了纯净语音和含噪语音 WPD1的瞬时能量谱，可以发现它们的瞬时能量谱差异较大；纯净语音的瞬时能量谱主要集中于语音区域；而含噪语音的瞬时能量谱在整个时间轴采样点上都有分布，但语音区域段的瞬时能量谱占主导地位，而噪声段瞬时能量谱相对语音区域较弱。因此语音和噪声的瞬时能量谱特征具有较好的区分度，后文将此特征作为语音端点检测的依据。

2.3 小波包分解在时频分析中的优势

为便于比较，本文对含噪语音分别按如下两种方法进行处理：（1）HHT变换；（2）小波包分解后的HHT变换，其结果如图2所示。图2（a-c）分别为含噪语音HHT边际谱、含噪语音 WPD1的边际谱以及含噪语音 WPD8的边际谱，未引入小波包分解的边际谱（图2（a））的频带范围分布较广，在整个频带范围都有分布，而引入小波包分解的WPD1和 WPD8的边际谱（图2（b，c））分布的频带范围较窄，分别集中于低频和高频段分布。由实验结果可知：小波包分解在含噪语音Hilbert谱分析中具有显著的优势，将频带范围细分，避免模态混叠，使其满足HHT模态的单一组分要求，由于小波包分解具有正交性与自适应性，从而提高EMD的分解能力，改善时频分辨率。

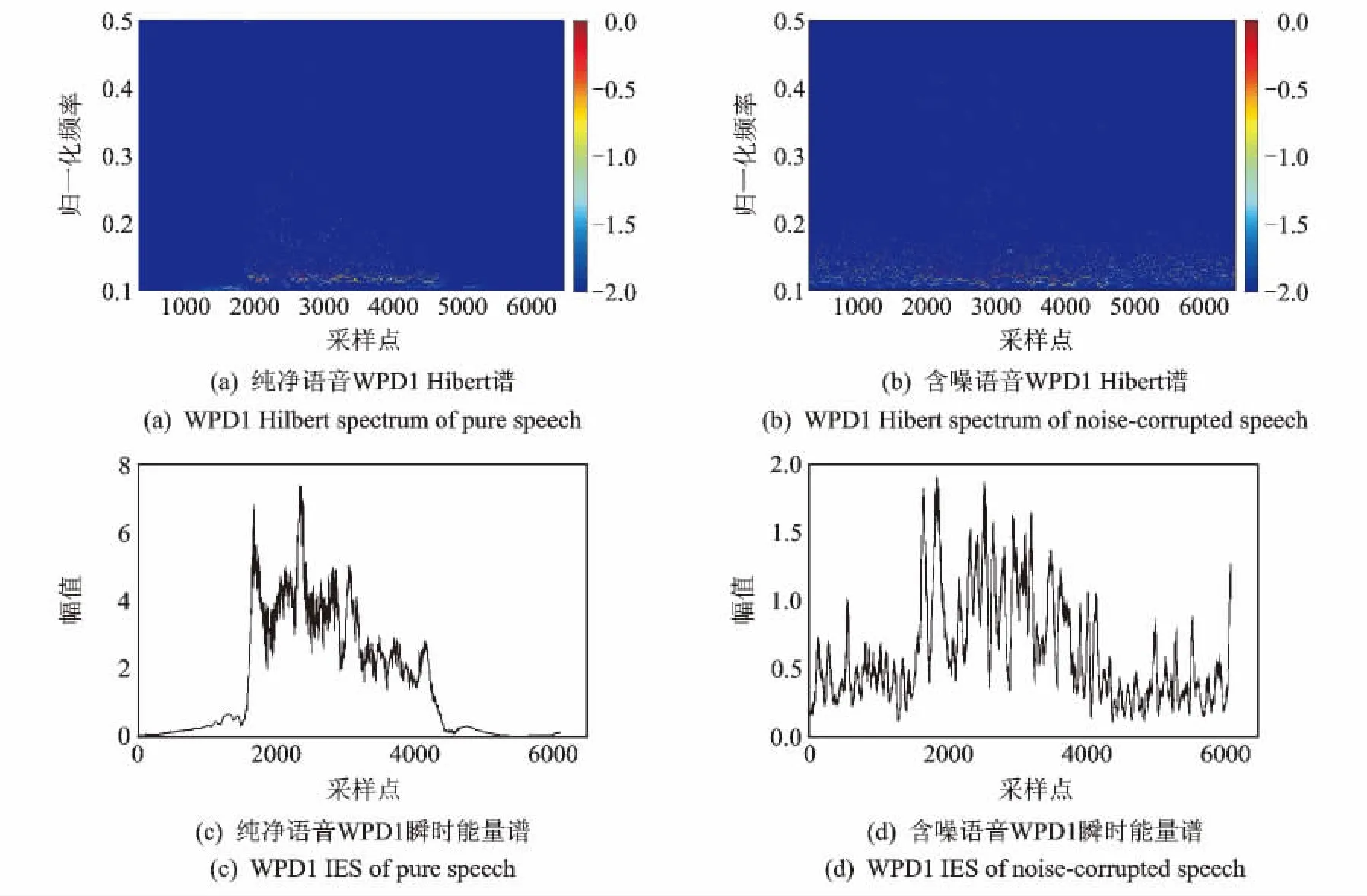
图1 纯净语音和含噪语音时频谱Fig.1 Time-frequency spectrum of pure speech and noise-corrupted speech

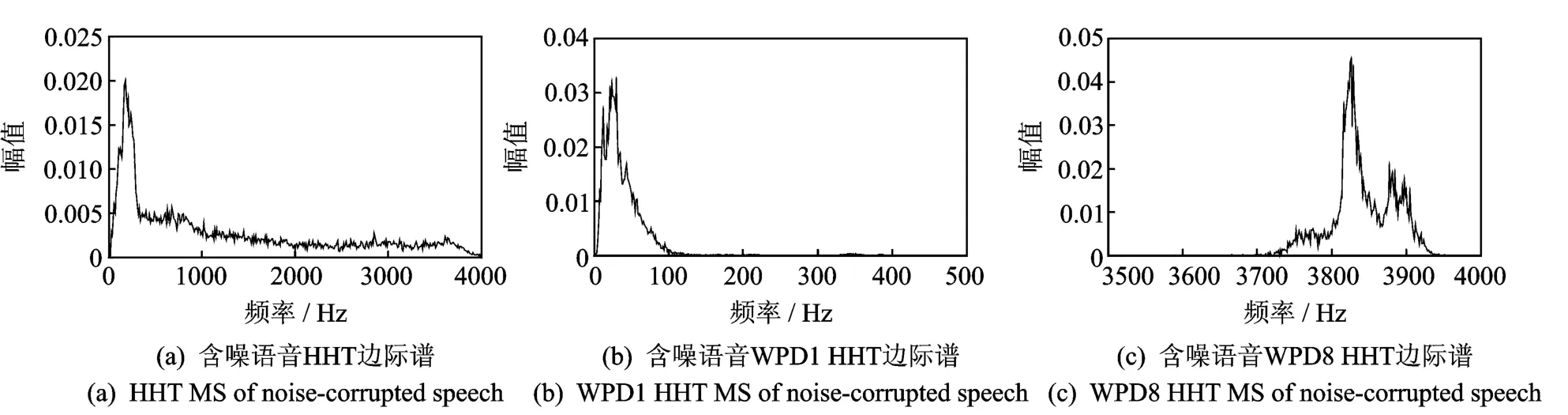
图2 含噪语音HHT边际谱和含噪语音WPD HHT边际谱Fig.2 HHT and WPD HHT marginal spectrum of noise-corrupted speech

2.4 基于瞬时能量谱特征的含噪语音端点检测

2.4.1 实验步骤

为了验证小波包分解HHT方法在分析含噪语音时频特征方面的有效性，本文提出了基于小波包分解的HHT变换瞬时能量谱方法，用于含噪语音的端点检测，详细步骤如下：

（1）对含噪语音进行预加重处理，选用db3小波基进行3层分解，将分解的信号重构记为WPDi（i＝1，2…，8）。

（2）对重构的 WPD1进行EMD分解并运用相关系数阈值准则筛选获得有效的IMF分量。

（3）对有效的IMF分量进行Hilbert变换并进行分帧处理。

（4）计算相应的瞬时能量谱E（t），将前5帧瞬时能量谱均值作为噪声能量谱Enoise。

（5）采用起-止双门限阈值法进行端点检测，若E（t）＜aEnoise，则继续检测，如果E（t）≥aEnoise，则记录为语音开始点，直到E（t）＜bEnoise，则记录为语音结束点；其中a和b分别为比例因子。

如果语音结束点与语音开始点之差小于长度阈值c，则认为检测得到的语音起点和终点均为干扰点，将它们舍弃；然后对后续瞬时能量谱序列继续重复步骤（5）进行语音端点检测，直到检测到有效的语音端点或语音序列结束为止。

2.4.2 实验结果与分析

设帧长为240，帧移为80，参数a＝1.5，b＝1，c＝5。在端点检测时，如果自动检测的前后端点与手工标定的端点差别在±5帧以内，则视为正确［10］。

为了说明本文方法的可行性，对不同类型以及不同强度的含噪语音引入传统广义维数（Original generalized dimension，OGD）以及谱熵（Spectral entropy，SE）的端点检测方法，如表2所示。可以发现，当信噪比为20db时，小波包分解的HHT瞬时能量谱算法的准确率要略低于传统广义维数和谱熵算法，但是当信噪比降到10db以下时，本文端点检测算法的准确率较其他两种算法具有显著的优势，尤其当信噪比为0db时，谱熵算法的准确率已经下降到50%左右，传统广义维数在70%左右，而本文的算法仍旧保持在90%左右（F16时只有74%，但是仍高于其他两种方法）。传统广义维数与谱熵算法在高信噪比的情况下，语音端点检测的效果较理想，但是对于信噪比较低的情况下，端点检测效果不是很理想，而本文的算法相对于信噪比的变化，端点检测效果较为稳定，具有较好的检测能力、自适应性及较强的鲁棒性。

表2 本文方法与传统方法的语音端点检测准确率对比表（%）Table 2 Correct rate comparison of speech endpoint detection with different methods（%）

3 结束语

本文提出对含噪语音信号进行小波包分解，以改善Hilbert-Huang变换方法的模态混叠问题，提高时频分辨率；另外提出相关系数阈值准则对IMF分量进行筛选，将避免Hilbert谱中出现的虚假频率。通过含噪语音的端点检测应用，验证了本文语音时频分析方法的有效性。本文方法将为后续语音复原、语音识别以及语音编码的研究提供一个新的思路。

［1］Kim K，Kim M Y.Robust speaker recognition against background noise in an enhanced multi-condition domain［J］.IEEE Transactions on Consumer E-lectronics，2010，56（3）：1684-1688.

［2］余华，黄程韦，金赟，等.基于粒子群优化神经网络的语音情感识别［J］.数据采集与处理，2011，26（1）：57-62.

Yu Hua，Huang Chengwei，Jin Yun，et al.Speech emotion recognition based on particle swarm optimizer neural network［J］.Journal of Data Acquisition and Processing，2011，26（1）：57-62.

［3］Backstrom T，Magi C.Effect of white-noise correction on linear predictive coding［J］.IEEE Signal Processing Letters，2007，14（2）：148-151.

［4］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proc.R.Soc.Lond.A，1998，454：903-995.

［5］Huang H，Pan J Q.Speech pitch determination based on Hilbert-Huang transform［J］.Signal Processing，2006，86（4）：792-803.

［6］Molla K I，Shaikh M，Hirose K.Time-frequency representation of audio signals using Hilbert spectrum with effective frequency scaling［C］∥Proceeding of 11th International Conference on Computer and Information Technology（ICCIT）. Khulna：IEEE，2008：335-340.

［7］Peng Z K，Tse P W，Chu F L.An improved Hilbert-Huang transform and its application in vibration signal analysis［J］.Journal of Sound and Vibration，2005，186（2）：187-205.

［8］Yuan L，Yang B H，Ma S W，et al.Combination of wavelet packet transform and Hilbert-Huang transform for recognition of continuous EEG in BCIs［C］∥Proceeding of the 2nd IEEE International Conference Computer Science and Information Technology.Beijing，China：IEEE，2009：594-599.

［9］Varga A.Assessment for automatic speech recognition：Ⅱ.NOISEX-92：A database and an experiment to study the effect of additive noise on speech recognition systems［J］.Speech Communication，1993，12（3）：247-251.

［10］武薇，范影乐，庞全.基于广义维数距离的语音端点检测方法［J］.电子与信息学报，2007，29（2）：465-468.

Wu Wei，Fan Yingle，Pang Quan.A speech endpoint detection method based on the feature distance of generalized dimension［J］.Journal of Electronics ＆Information Technology，2007，29（2）：465-468.