基于边缘检测的双树复小波图像融合算法

李莉

（华侨大学 厦门工学院，福建 厦门 361021）

0 引言

图像融合[1-3]指对多幅源自于同一场景的图像进行综合，以获取更好的视觉效果和易于机器识别为目的，产生比单一信源更精确、更完全、更可靠的图像。图像融合属于信息融合的一个分支，能够有效地去除参与融合的多幅图像中冗余或干扰信息，反映多幅源图像的信息，使获得的图像更加准确、完整，便于更综合、全面地判断和分析图像，弥补了单一成像系统的不足。20世纪70年代后期提出图像融合概念后，国内外对图像融合算法的研究以及相关应用的探讨已取得了长足的发展。图像融合处理可在像素级、特征级以及决策级三个层面上进行，图像的像素级融合主要可分为两类：基于空域和基于变换域。随着小波变换理论的完善，基于小波的图像融合方法已成为国内外像素级图像融合方法的研究热点[4-7]。目前，大多数的小波变换图像融合算法主要是针对高频信息的融合规则进行讨论，对低频信息仅采取简单的加权平均融合规则。然而，图像经过小波变换后，主要的能量都包含在低频信息中，融合的质量很大程度上都取决于低频信息融合规则的选取。因此，对低频信息的融合规则研究具有相当重要的意义。

传统的离散小波变换（DWT）存在平移敏感性和缺乏方向选择性等缺陷，严重地影响了小波域信号处理效果。IVAN W S[8]等人提出的双树复小波变换 （DTCWT）成功地解决了传统DWT的缺陷，并已成功应用于图像融合领域[9-11]。本文针对双树复小波变换以及低频信息融合规则进行研究，提出了一种新的图像融合算法——基于边缘检测的双树复小波图像融合算法。该算法能够有效提高图像融合的清晰度及质量。

1 双树复小波变换

双树复小波变换 （DT-CWT）结构示意图如图1所示。当对应小波基（图1中的h0和g0、h1和g1）近似满足Hilbert变换关系时，双树复小波变换能够近似满足平移不变性，并具有良好的方向选择性。在二维双树复小波变换中实部与虚部都具有6个方向子带，分别指向±15°，±45°和±75°方向。这些优点使双树复小波变换为图像融合提供了更好的条件。

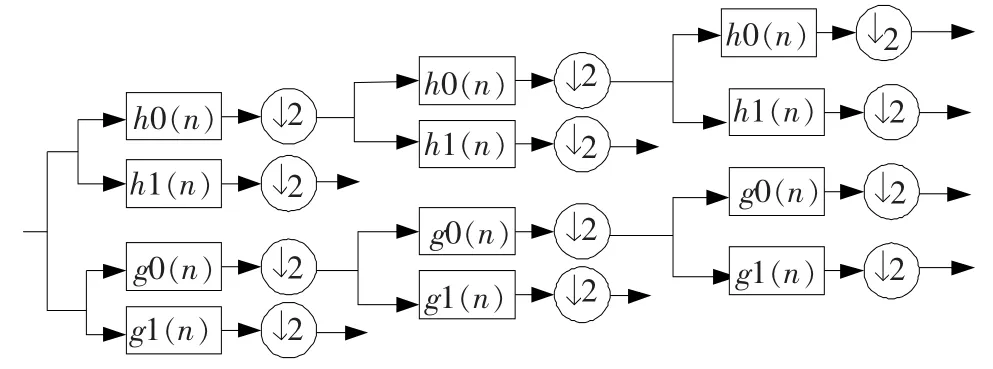
图1 三层一维双树复小波变换示意图

2 融合规则

基于小波变换的图像融合方法基本思想如图2所示。先对源图像进行小波分解，得到不同频率的不同特征域的图像表示，在各个特征域上选取不同的融合规则或融合方法进行图像的融合，融合后得到新的小波系数经逆小波变换得到融合后的图像。

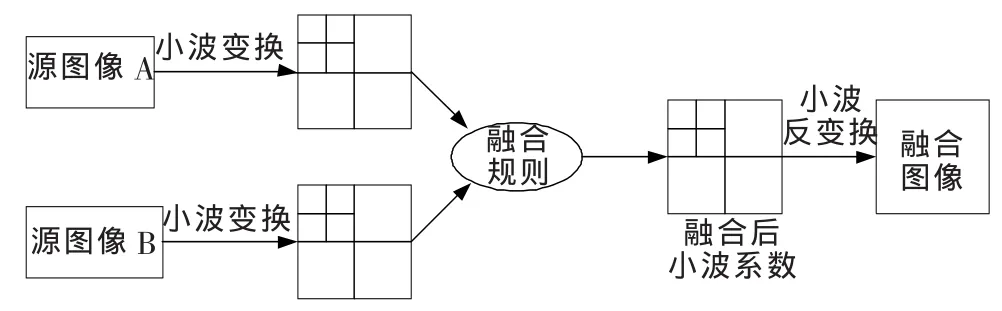
图2 基于小波变换图像融合方法示意图

2.1 低频信息融合规则

图像经过小波变换后，其主要能量集中在低频区域中，传统的加权平均选取融合算法可以有效地抑制图像噪声，但图像边缘特征信息却被忽略，造成融合图像的特征信息丢失、融合图像质量下降。本文在传统小波图像融合基础上，对传统的低频系数加权平均算法进行改进，提出了基于边缘检测的低频系数图像融合方法。该算法在多源图像中最大可能地选取边缘点加以保留，可使融合后图像的细节更加丰富。经典的边缘检测算子包括Sobel算子、Roberts算子、Canny算子、Laplacian算子以及Prewitt算子等，这些算子均在像素级上进行图像边缘检测，并且都有一定的局限性。例如，Laplacian算子虽然对细线和孤立点的检测效果较好，但对噪声比较敏感；Prewitt和Sobel算子则是对渐变灰度和低噪声效果显著，但是检测边缘较粗且定位较差。Zernike正交矩的亚像素边缘检测方法[12-13]的提出很大程度上提高了边缘检测的精准度。本文利用Zernike正交矩的亚像素边缘检测方法对图像小波分解后的低频信息进行边缘检测，获取最佳边缘信息。

具体融合规则如下：

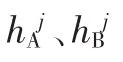
2.2 高频信息融合规则

图像经过小波分解后，低频分量反映了图像的基本概貌，高频分量则突出了图像的细节信息。由于图像的局域特征往往不能由单一像素所表征，因此，基于区域特征的融合规则也一直是研究的热点。本文选取两种基于区域特征的融合规则对高频信息进行融合：区域能量最大值法和区域边缘强度最大值法。

第k个源图像的高频小波系数中以（x，y）为中心、大小为M×N的区域的能量ENj（x，y）表示为：

区域中值定义为：

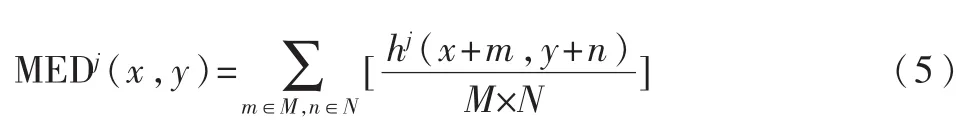
则第k个图像的像素（x，y）在j尺度下，窗口大小为M×N的边缘强度[3]定义为：

本文所选取的两种区域特征融合算法的窗口大小均为3×3，两种高频系数具有如下融合规则：

方法1：区域能量最大值法

其中，hA和hB分别代表源图像A和B的高频系数，Fh表示融合后的高频小波系数，dA和dB则为权系数，取值为：

方法2：区域边缘强度最大值法

基于区域边缘强度最大值法的基本思路与区域能量最大值法一致，在两个源图像的高频小波系数中根据区域边缘强度的大小来选择谁作为融合后的小波系数。区别仅在于权系数的取值准则不同：

3 实验结果与分析

本文选取常见的多聚焦图像cameraman进行融合，为了验证所提出的融合算法的有效性与优越性，采用以下4种方法对比本文所提出的算法的性能。

方法1：低频系数采取加权平均法，高频系数选用区域能量最大法进行融合。

方法2：低频系数采取边缘检测法，高频系数选用区域能量最大法进行融合。

方法3：低频系数采取加权平均法，高频系数选用区域边缘强度最大值法。

方法4：低频系数采取边缘检测法，高频系数选用区域边缘强度最大值法。

实验中采用的融合评测方法有熵、峰值信噪比（PSNR）、平均梯度以及标准差。熵值越大，表明所含信息量越大；PSNR越大，表明所获取的信息越多、噪声越小，融合的效果也越好；平均梯度越大，表明图像的细节部分越丰富，图像清晰度越高；标准差越大，表明图像灰度值相对于图像均值越分散，图像的反差越大，所包含的图像信息量越多。

表1列出了本文所采取的4种方法的融合效果。图3展示出了效果最好的方法2的融合效果图。对比这4种方法的各项指标不难发现，方法2的熵值、PSNR以及平均梯度3个指标均优于其他方法，标准差基本一致。从实验结果可看出，高频系数选用相同融合规则时，低频系数采用边缘检测方法进行融合效果较好，说明本文提出的基于边缘检测的融合算法具有一定的优越性，边缘与细节信息保留较好。低频系数的选择决定了融合图像的视觉效果，采用本文算法可更大限度地获取并保留图像的细节与纹理信息，增强融合图像的质量。

表1 融合实验效果对比

图3 融合效果图（方法2）

4 结论

本文提出了一种新的图像融合算法——基于边缘检测的双树复小波图像融合算法。采用双树复小波变换，可有效克服传统离散小波变换存在的平移敏感性和缺乏方向选择性等缺陷；低频系数融合规则结合了边缘检测的方法来降低边缘细节信息的丢失，提高图像融合的清晰度及质量；高频系数采用常见的区域能量最大法以及区域边缘强度最大值法进行融合。实验结果利用4个客观评价标准进行定性衡量，证明了本文算法的有效性和正确性。

[1]POHL C，VAN GENDEREN J L.Multisensor image fusion in remote sensing：concepts，methods and applications[J].International Journal of Remote Sensing，1998，19（5）：823-854.

[2]郭雷，李晖晖，鲍永生.图像融合[M].北京：电子工业出版社，2008.

[3]闫敬文.数字图像处理MATLAB版（第二版）[M].北京：国防工业出版社，2011.

[4]刘海涛，石跃祥，康蕴.基于小波分析的图像融合新方法[J].计算机工程与应用，2013，49（6）：205-208.

[5]Zhang Qiang.Multi-focus image fusion using the nonsubsampled Contourlet transform[J].Signal Processing，2009，89（7）：1334-1346.

[6]ChenGuangqiu，GaoYinhan.Multisourceimagefusion based on double density dual-tree complex wavelet transform[C].InternationalConferenceonFuzzySystemsand Knowledge Discovery（FSKD），2012：1864-1868.

[7]吴华，王海顺.基于小波变换和Sobel算子图像融合算法研究[J].计算机仿真，2011，28（10）：232-235.

[8]IVAN W S，RICHARD G B，NICK G K.The dual-tree complex wavelet transform[J].IEEE Signal Processing Magazine，2005，11（22）：123-151.

[9]HILL P，CANAGARAJAH N，BULL D.Image fusion using complex wavelets[C].Proceedings of the British Machine Conference，Cardiff，2002：487-496.

[10]王亚杰，李殿起，徐心和.基于双树复小波变换的图像融合方法[J].计算机工程，2008，34（15）：176-178.

[11]陶玲瑶，弓晓锋.基于DT-CWT的图像融合算法研究[J].通信技术，2011，44（12）：104-106.

[12]GHOSAL S，MEHROTRA R.Orthogonal moment operators for subpixel edge detection[J].Pattern Recognition，1993，26：295-306.

[13]Ding Xinghao，Deng Shanxi，Yang Yongyue，et al.Subpixel detection based on spatial moment and Zernike moment[J].Journal of Applied Sciences，2004，22（2）：191-194.