样本-属性加权的朴素贝叶斯改进算法
曾文赋(福建省福州第一中学,福建 福州350001)
分类是通过分析训练数据样本,生成分类函数或模型,通过模型将数据库中的数据映射到某一类别中,产生数据关于类别的精确描述。
朴素贝叶斯算法作为一种最简单、有效且在实际使用中很成功的分类算法,其性能可与神经网络、决策树相媲美[1]。它发源于古典数学理论,具有坚实的理论基础,与其他方法相比有较小的误差率,并广泛应用于数据挖掘、自然语言处理、医疗研究等众多领域。例如,潘志方提出一种可根据用户的网页访问记录和网上交易记录来动态地对顾客进行分类的方法[2];刘青[3]等通过不断改变EM算法的收敛初始条件以提高收敛效果,并结合朴素贝叶斯分类方法对未标记的中文网页进行分类;张丽伟[4]等用遗传算法对朴素贝叶斯分类算法进行改进,使之能够较好地鉴别诊断病患所属的症候,比较分析改进前后的识别效率。
朴素贝叶斯算法主要通过假设待考查的变量遵循某种概率分布,根据这些概率和已观测到的数据进行推理,作出最优决策。算法基于条件独立性假设,即假定特征向量的各分量间相对于决策变量相对独立,然而在实际应用中该假设并不现实,从而影响其分类性能。
1 朴素贝叶斯算法描述
设每个数据具有k个属性,用向量a=[a1,a2,…,ak]描述, 其中a1,a2,…,ak分别表示样本在属性A1,A2,…,Ak上的值。假设数据有m个类,分别用V1,V2,…,Vm来表示。给定一个样本,可得到最可能的目标值如下:
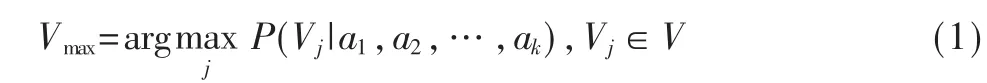
对一个未知数据样本x=[x1,x2,…,xk],由贝叶斯定理得:

结合贝叶斯定理、条件独立假设和P(x)对所有类均为常数,可判断x的类别如下:

综上,根据朴素贝叶斯算法,对于一个未分类的样本x,只需分别计算出P(Vj)和 x属于类别Vj的先验概率P(x|Vj),再选出式(3)中概率最大的那个类即为x的类别。
2 改进策略及算法描述
由于朴素贝叶斯算法假设数据遵循某种概率分布,认为条件属性对决策属性的重要程度均相同且须满足条件独立性假设等,这些都会影响其在实际应用中的分类性能。在实际应用中,不同属性对分类影响的效果是不同的,故改进算法中考虑对不同的属性给予不同的权值,定义属性权刻画条件属性对决策属性的重要性,以克服条件独立性假设的缺陷,从而扩展朴素贝叶斯算法;同时,通过属性权结合信息熵获得样本熵权,对原始数据样本进行修正,提高算法的泛化能力。
2.1 属性权计算
训练数据集由条件属性和决策属性来描述[5],对不同的条件属性进行加权,通过计算条件属性和决策属性间的相关系数表示两者间的相关度,得到属性权WA。
假设X=(X1,X2,…,Xk)表示k个条件属性,Y表示决策属性。计算Xi和Y的相关系数如下:

其中 Cov(Xi,Y)为Xi和Y的协方差,D(Xi)、D(Y)分别为Xi和Y的方差。可知,属性权WAi的值越大,表示第i个条件属性对分类的影响越大。
2.2 样本熵权计算
信息熵由香农所提出[6],用来度量不确定的信息量(随机性)的大小,故计算信息熵等价于确定随机变量的分布。假设一个数据样本x=(x1,x2,…,xk),结合信息熵和2.1节中所定义的属性权计算样本熵权如下:

通过结合属性权和信息熵定义样本熵权WS(x),融合属性信息修正原始数据样本以提高泛化能力。
2.3 样本-属性加权的朴素贝叶斯算法描述
设数据集X中包含n个数据样本,每个数据样本具有k个属性,第i个样本可表示为Xi=(Xi1,Xi2,…,Xik),i=1,2,…,n。X中含有m个类,用V1,V2,…,Vm来表示。样本-属性加权的朴素贝叶斯算法步骤描述如下:
(1)对原始数据集X中的属性,由 2.1节计算出属性权 WA;
(2)对原始数据集X中的每个样本,由2.2节计算出样本熵权,记为WS;
(3)利用步骤(2)中计算获得的已融合属性信息的样本熵权WS,对数据集X进行加权,得到修正后的数据集X′,使得X′相比于X具有更好的泛化能力;
(4)对修正后的数据集X′,使用式(6)的加权朴素贝叶斯分类模型进行分类,得到分类结果:

其中P(Vj)和P(xi|Vj)可由修正后数据集X′中获得,加权朴素贝叶斯分类模型的加权因子WAi即为步骤(1)中计算获得的属性权。
3 实验结果与分析
实验数据采用UCI机器学习数据库中的16个数据集,在Matlab开发环境中完成调试,对各个数据集分别使用朴素贝叶斯算法和样本-属性加权的朴素贝叶斯算法采用十折交叉验证方式比较其分类性能。
表1列出了实验所使用的各个数据集名、样本数、属性数和两种算法分类的准确率。
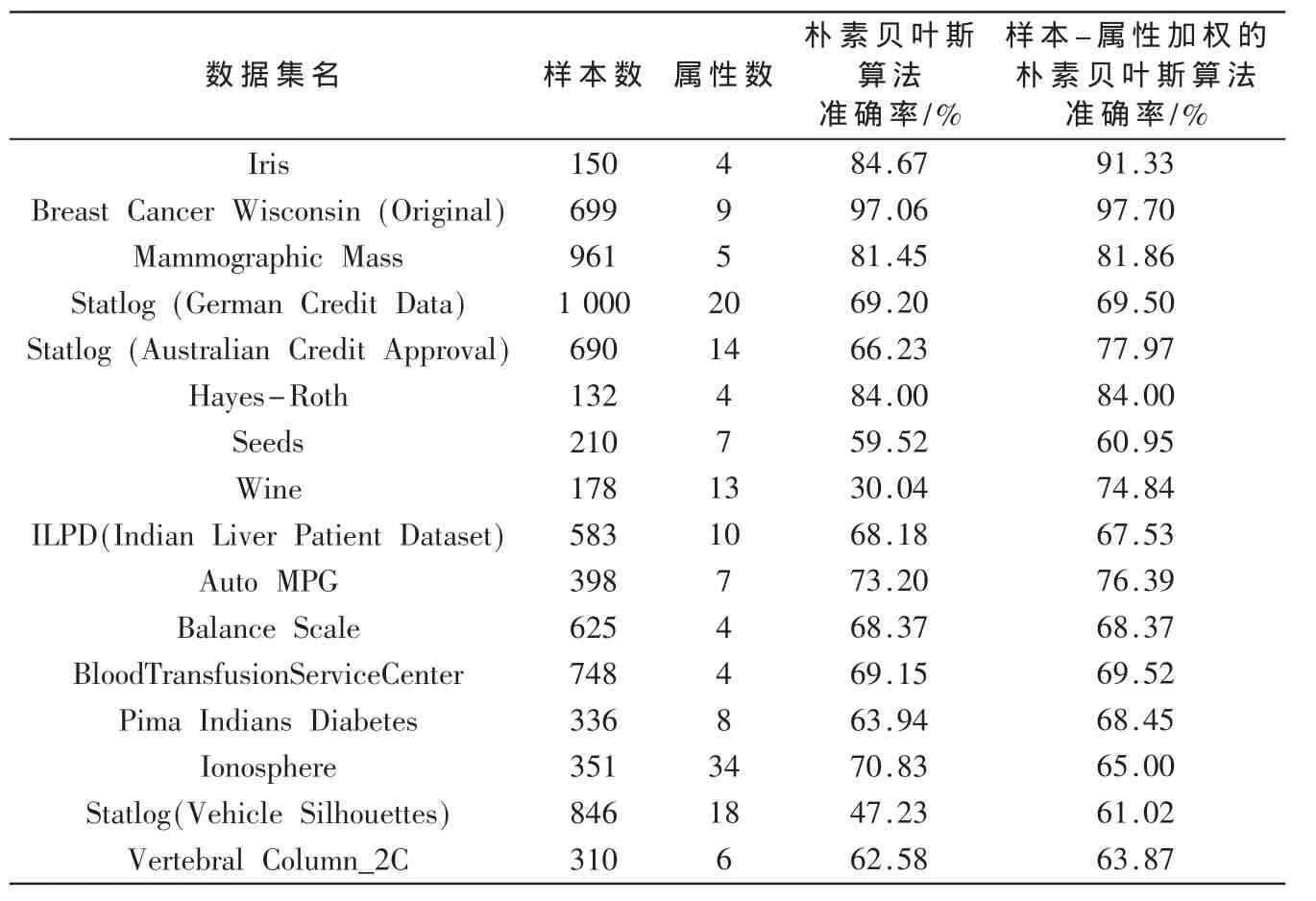
表1 数据集信息及两种算法比较
由上表可知,改进算法在实验中所使用的12个数据集分类准确率与朴素贝叶斯算法相比均有不同程度的提高;且在两个数据集上准确率相同;另外,有两个数据集的准确率低于朴素贝叶斯算法。总体上看,样本-属性加权的朴素贝叶斯算法与朴素贝叶斯算法相比具有更好的分类性能。
本文对朴素贝叶斯算法进行改进,给出了样本-属性加权的朴素贝叶斯算法,在UCI数据集上进行实验,验证了改进算法相比于原算法具有更好的分类性能。
[1]LANGLEY P,IBA W,THOMPSON K.An analysis of Bayesian classifiers[C].In:Proc of the 10th National Conference on Artificial Intelligence.MenloPark:AAA I Press,1992:223-228.
[2]潘志方.基于朴素贝叶斯学习的电子商务网站客户兴趣分类的应用研究[J].计算机科学,2007,34(6):214-215,222.
[3]刘青,何政.结合EM算法的朴素贝叶斯方法在中文网页分类上的应用[J].计算机工程与科学,2005,27(7):65-66,90.
[4]张丽伟,段禅伦,熊志伟,等.朴素贝叶斯方法在中医证候分类识别中的应用研究[J].内蒙古大学学报,2007,38(5):568-571.
[5]宫秀军,刘少辉,史忠植.一种增量贝叶斯分类模型[J].计算机学报,2002,25(6):645-650.
[6]Zhang Jiguo,Zhu Yongzhong.Information entropy measures for fuzziness[J].Journal of Hohai University Changzhou,2001,15(4):16-21.

