地铁隧道两井联系测量严密平差及软件实现

范朋飞 石德斌

(铁道第三勘察设计院集团有限公司，天津 300251)

地铁隧道两井联系测量严密平差及软件实现

范朋飞 石德斌

(铁道第三勘察设计院集团有限公司，天津 300251)

介绍两井联系测量钢丝投点法的工作原理与技术要点，依据无定向导线的特性采用附有参数的条件严密平差，最后通过程序实现数据自动化处理，并结合具体工程进行验算分析。

联系测量 无定向导线 平差 软件

地铁建设测量中联系测量始终发挥着至关重要的作用，通过它可以建立地面控制点与地下控制点的对应关系，获取地下控制点坐标及控制边方位角，实现地下工程施工的精密控制。目前联系测量方法较多，均有各自的特点和使用范围，两井联系测量钢丝投点法是一种过程简单快捷、对现场生产影响较小的联系测量方法，在地铁联系测量中得到很好的应用。

1 两井联系测量

两井联系测量钢丝投点法是一种结合联系三角形法和投点法各自特点形成的一种无定向联系测量方法。相比一井联系三角形法，大大拉长了两根钢丝的间距，减小钢丝投点误差对井下导线的横向位置影响。如图1是深圳地铁9号线某车站的两井联系测量示意，井上通过近井控制点观测角度和距离获得两钢丝坐标，井下通过在控制点架设仪器观测两钢丝，组成无定向导线，通过钢丝坐标推算井下控制点坐标及控制边方位角。

图2为无定向附合导线通用示意，端点G1和G2为已知点，中间连接有n个待定点，必要观测个数为2n，已有n个观测角和n+1条观测边，因此剩余1个多余观测条件，该条件即从G1点到G2点的坐标闭合条件。该导线中没有方位角，很难列出条件方程，因此引入起始方位角参数，即引入起始边G1-1的方位角T，通过方位角传递计算坐标增量，从而形成坐标闭合条件。基于以上分析，将采用“附有参数的条件平差”方法，对无定向附合导线进行严密平差。

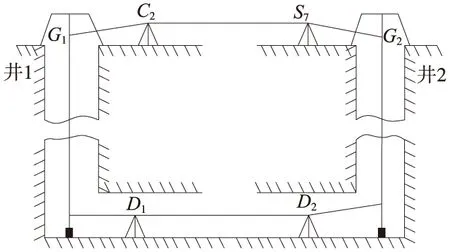
图1 两井联系测量示意

2 无定向附合导线严密平差

2.1 近似坐标及方位角计算

以G1点为原点任意假定坐标系，设G1-1边的方位角为0，则根据导线观测角度，可推算其他边的方位角，根据假定坐标系下的方位角和观测距离可计算出G2点在假定坐标系中的坐标

(1)

可得假定坐标系和实际工程坐标系之间的夹角为

(2)

前面已经假设G1-1边的方位角为0，因此T0即为起始边G1-1的近似方位角，其余边的近似方位角可用下式计算

(3)

其中，αSi为Si边的方位角，βi-1为Si-1边和Si边的左夹角。

根据各边的近似方位角和观测距离可计算待定点的近似坐标

(4)

2.2 附有参数的条件方程

根据G1和G2的坐标闭合条件，可列下面条件方程

(5)

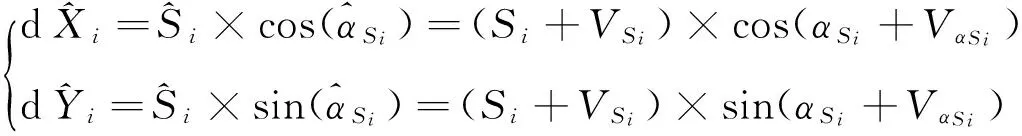
(6)

式中，VSi为边长Si的改正数，VαSi为方位角αSi的改正数。

对式(6)进行线性化，得

(7)

由公式(3)可知

(8)

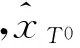
结合公式(3)和(8)可得

(9)

将(9)代入(7)得

(10)

将(10)代入(5)中整理后得

(11)

式中，WX和WY为坐标闭合差，具体形式为

(12)

附有参数的条件平差的一般形式为

(13)

将条件方程(11)化为矩阵形式为

(14)

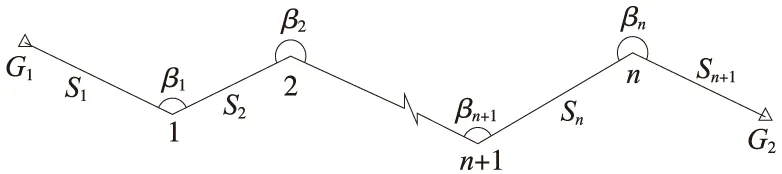
图2 无定向附合导线示意

2.3 观测值权的确定

无定向附合导线没有方位角条件，因此无法通过方位角闭合差计算获取测角中误差mβ，通常依据仪器的测角精度、测回数及外部观测条件等因素估算，测距中误差可采用式(15)进行计算

(15)

式中，a为测距仪器的标称固定误差，b为比例误差，Si为观测的距离。

测角观测精度相同，令测角中误差mβ为单位权中误差，则角度的权为Pβ=1，边长的权为PSi=m2βm2Si。

3 软件编程及算例分析

根据上面介绍的附有参数的条件平差理论，采用Visual Basic6.0开发工具，设计研制了“两井无定向导线平差”软件，该软件集数据读取、编辑、处理、绘图、报表为一体，为数据处理提供了很好的帮助。

3.1 功能设计与数据处理流程

该软件主要功能包括：数据读取、编辑，数据平差处理，网图绘制及保存，数据及平差报表的查看。软件设计简单快捷，无需安装且支持多种操作系统使用。数据处理流程见图3，软件主界面见图4。

图3 数据处理流程

图4 软件界面

3.2 算例分析

数据来自深圳地铁9号线某车站的两井联系测量数据，如图1所示，钢丝坐标通过地面控制点C2和S7解算获得，井下以钢丝G1和G2为已知点，通过在D1和D2分别架设仪器，观测相应角度和距离，组成无定向导线，解算地下控制点D1和D2的坐标及D1-D2边的方位角。观测数据见表1。

表1 联系测量观测数据记录表

观测值定权参照仪器标称精度，本次工程中测距标称精度为±(2+2×10-6D) mm，仪器标称测角中误差为±0.5″。使用编制的软件对数据进行解算，得到坐标闭合差为Wx=-1.04 mm，Wy=-0.06 mm，相对闭合差为1/88 520<1/35 000(城市轨道交通精密导线测量技术要求)，满足地铁联系测量规范要求。

4 结论

通过对无定向导线严密平差理论的研究及软件编程，并结合具体工程进行验算，得到以下结论：

(1)两井联系测量大大拉长了钢丝间距，减小了钢丝投点误差造成的横向偏差。因此，在实际工程应用中应尽量将无定向导线布设成沿线路方向的直伸导线形式，以减小最终横向贯通误差。

(2)附有参数的条件平差在无定向导线平差中应用比较合理，起到了严密平差的效果。

(3)采用VB开发工具进行编程，界面可视化强，算法编写方便，成图简单，在本次工程应用中发挥了很好的作用。

[1] 杨柳，左志刚.地铁平面联系测量方法研究[J].铁道勘察，2012(3)：14-16

[2] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社，2003

[3] 罗三明，万文妮，高培芝.盾构工程竖井联系测量数据处理方法研究[J].大地测量与地球动力学，2007(5):123-127

[4] 何波，刘成龙，黄志伟，等.全站仪竖井联系测量的平差计算原理及其精度分析[J].铁道勘察，2010(3)：17-20

[5] 张俭为.双井定向的原理在隧道贯通测量中的应用[J].江西测绘，2008(3)：63-64

[6] GB 50308—2008城市轨道交通工程测量规范[S]

[7] 姬晓旭，刘成龙，何波.竖井联系测量的新方法及其应用[J].铁道勘察，2009(5)：14-17

[8] 李军.竖井定向联系测量新方法的应用研究[J].测绘通报，2005(8)：44-46

TheRigorousAdjustmentandSoftwareofConnectionSurveyaboutTwin-wellintheMetroTunnel

FAN Peng-fei SHI De-bin

2014-06-30

范朋飞(1987—)，男，2013年毕业于长安大学地质工程与测绘学院，硕士，助理工程师。

1672-7479(2014)05-0012-03

U452.1+3

： B