对一道中考重组题的评析与讲评

☉江苏省海安县新生初级中学 朱月凤

在数学的天地里，重要的不是知道什么，而是让人怎么知道什么——毕达哥拉斯.此话意在说明例题教学，重要的不是仅提供题目答案，而是引导学生发现解题的线索和路径，归纳出解题方法，举一反三，达到“会当悟解法，一览众题易”的境界.现通过对一道中考模拟压轴题的评析和讲评案例的反思说明笔者对此的理解.

一、试题呈现

引例 （2012年江苏省海安县中考模拟试题）如图1所示，E为矩形ABCD的边AD上一点，动点P、Q同时从点B出发，点P沿折线BE－ED－DC运动到点C时停止，点Q沿BC运动到点C时停止，它们运动的速度都是1cm/s.设P、Q同时出发ts时，△BPQ的面积为ycm2.已知y与t的函数关系图像如图2（抛物线的一部分）所示.

（1）当0＜t≤5时，求抛物线（曲线OM）的解析式；

（2）求BE和∠ABE的正切值；

（3）求t为何值时，△BPQ是直角三角形？

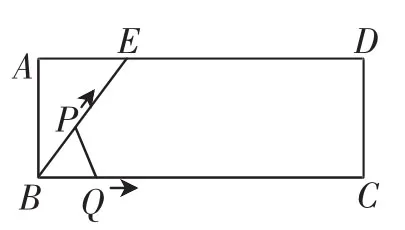
图1

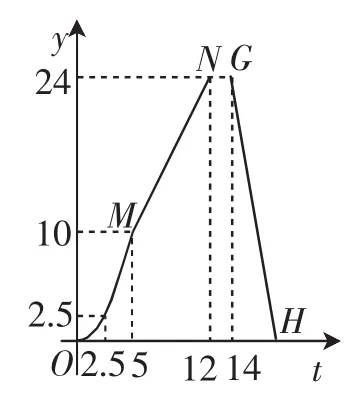
图2

二、试题评析

运动与变化是数学之精髓，更是数学之美的集中体现，数学中普遍存在着动与静的对立统一的辩证关系，本题命题者独具匠心地将两个“质点”的运动融入其中，由于质点运动的路径不同，时间的差异构成三角形的多样性，让考生探索发现其中某些特殊位置能构成直角三角形时的质点运动的时间.这就要求应试者不但具有洞察图形结构的识图能力，更是需要有结合图形分析构成直角三角形时质点P、Q可能存在的位置，然后根据直角三角形三边关系借助勾股定理构造一元二次方程求出时间t，其中蕴含数形结合思想，对于第（3）问，根据题目提供的质点P、Q运动的可能路径可以发现△BPQ的形状有四种情形，所以应结合图形分类探究，从探究的结果看有三种不同的结果.本题用代数的方法研究几何问题，通过数与形的对应和转化，实现具体形象与代数之间的联系，也就是几何问题代数化，而数形结合及方程思想可以化难为易，使抽象的演绎推理通过简单的代数计算巧妙获解.这样的试题能激发学生在更广阔的数学空间中探索几何图形所具有的性质，让学生在动态的图形中运用“静与动”的辩证关系探索研究问题的解题方法，感悟它们之间内在的相依关系，达到“做一题，通一类，会一片”，体验到“会当领解法，一览众题易”的较高解题意境.

三、困境寻因

笔者曾随机抽100份样卷，发现此题得分情况如下表：

得分情况 0分 1～4分 5～9分 10～12分 13～14分人数 52人 13人 22人 11人 2人

从上表不难看出，大多数同学对这种以图示形式给出条件的问题，束手无策，10%的同学只掌握基本的三点式确定二次函数解析式.20%的同学能进行简单的数形结合，但不会分离目标图形，进行分类讨论.还有10%的同学在进行分类讨论时，因为分类标准选择不当，例如，按点P、Q的位置，或按运动时间t，或按△BPQ中某一个角为直角进行讨论，造成失分.也有少数同学因为分类不周而失分.

四、讲评案例

师：读题干、读图1，你知道点P，Q是如何运动的吗？△BPQ的形状是如何变化的吗？

图3

生1：如图3，PQ有四种可能位置，因点P、Q运动的速度都是1cm/s，所以在点P到达点E之前，BP=BQ，此时△BPQ为等腰三角形，如△BP1Q1；接着在点Q运动到点C之前，因BE+EP=BQ，所以△BPQ的形状发生变化，不再是等腰三角形，如△BP2Q2；随后点Q停在点C处，点P一直运动到点D，△BPQ的形状依旧在变化，如△BP3C；最后点Q停在点C处，点P一直从点D运动到点C，此时△BPQ的形状一直是直角三角形，如△BP4C.

师：这位同学读题非常认真，观察极为仔细，这为本题的分类讨论打下良好的基础，值得大家学习.接下来请同学们观察图2，由此图你能发现△BPQ的面积的变化有哪几种不同的类型？

生2：△BPQ的面积的变化有抛物线型、直线型、常数型三种不同的类型.

师：对，结合图3，同学们能发现△BPQ的面积发生这几种变化的原因吗？

生3：当点P到达点E之前，BP=BQ，此时△BPQ为等腰三角形，此时△BPQ的底BQ在变，BQ边上的高在变，面积成两个变量的乘积，故图像为抛物线；接着在点P、Q继续运动，点Q运动到点C之前，△BPQ的底BQ在变，而BQ边上的高不变，故面积的变化呈直线型；当点Q停在点C处，点P继续运动到点D时，△BPQ的底BQ不变，BQ边上的高也不变，所以面积是常数；最后点Q停在点C处，点P一直从点D运动到点C时，△BPQ的底BQ不变，BQ边上的高变小，所以面积变化呈直线型.

师：了不起，思路很清晰.接下来请观察图2，你能说出坐标轴、图像转折点所表示的实际意义吗？

生4：如图2，横轴表示运动的时间，纵轴表示△BPQ的面积，点（2.5，2.5）表示当点P、Q运动2.5s时，△BPQ的面积为2.5cm2；点M表示当点P、Q运动5s时，△BPQ的面积为10cm2；点N、G分别表示当点P、Q运动12s、14s时，△BPQ的面积均为24cm2.

师：精彩，这位同学抓住了数形结合的要点，道出了关键点所表示的实际意义.再观察图1、图2，你能将图像转折点的坐标转化为线段长，并在图1中标出来吗？

生5：由图2中的点M（5，10）可知，图1中的BE=5，AB=4，根据勾股定理可得AE=3.由N（12，24），可知BC=12.

师：这位同学成功地将点的坐标转化成线段长，标注如图4所示，我们称之为标常量.观察图5，当点P、Q运动到图5所示的位置时，你能用含t的关系式表示BQ、EP、PK的长吗？并将它们分别标在图5上吗？

图4

图5

生6：BQ=t，EP=t－5，PK=2.标注如图5所示.

师：完全正确.哪位同学能在图6中用含t的关系式标注各有关线段的长呢？

图6

生7：标注如图6.

师：那么第（3）问该如何解答呢？请同学结合图3、图4、图5、图6，试着用分类讨论和方程思想解答，10分钟后我们用投影仪展示同学的答案.

……

师：时间到，请同学放下笔，我们一起看两位同学的满分解答.

生8：①当点P在BE上、点Q在BC上运动时，因为BP=BQ，∠PBQ不是直角，所以△BPQ不可能是直角三角形.

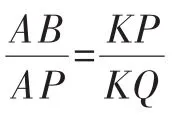
④当点P在DC上运动、点Q停在点C，即14≤t＜18时，△BPQ是直角三角形.

综上所述，当t=10或t=8+2或 14≤t＜18时，△BPQ是直角三角形.

师：该同学充分利用图3的四种可能，以点P、Q运动的位置为界，进行分类讨论，在观察图4、图5时，敏锐地发现“K型”图，利用相似三角形得比例式，从而建立所求量与已知量与之间的等量关系，顺利得出结果，很好.是否还有别的解法呢？请看生9的满分解答.

生9：①当0＜t＜5时，因为BP=BQ，∠PBQ不是直角，所以△BPQ不可能是直角三角形.

②当5≤t＜12时，如图5，因为BQ为最大边，所以∠BPQ=90°，所以BQ2=BP2+PQ2.因为BP2=AB2+AP2=42+（t－2）2，PQ2=22+42，BQ2=t2，所以t2=42+（t－2）2+22+42，解得t=10.

③当12≤t＜14时，如图6，因为BQ为最大边，所以∠BPQ=90°，所以BQ2=BP2+PQ2.因为BP2=AB2+AP2=42+（t－2）2，PQ2=（14－t）2+42，BQ2=122，所以122=42+（t－2）2+（14－t）2+42，解得t1=8－2（ 舍去），t2=8+2.

④当14≤t＜18时，△BPQ是直角三角形.

综上所述，当t=10或t=8+2或 14≤t＜18时，△BPQ是直角三角形.

师：该同学利用图3的四种可能，以运动时间为界，进行分类讨论，并利用勾股定理建立所求量与已知量之间的等量关系，顺利得出结果，也很好.

五、题后反思

这是一道动态几何问题，它是以运动的观点探究几何图形部分变化规律的问题.其特点是图形中的某些元素（点、线段、角等）或某部分图形按一定的规律运动变化，从而又引起了其他一些元素的数量关系、位置关系、图形重叠部分的面积或某部分图形的形状等发生变化.这类问题往往融几何、代数于一体，用到的知识点有相似三角形、勾股定理、四边形的有关定理、面积关系等，解题过程中渗透着数形结合、分类讨论、函数与方程、转化等思想.动态问题依托图形的变化，能很好地考查学生学习数学的探究能力与空间想象能力，体现试题的开放性与综合性，有较好的区分度与选拔功能.

综合性问题是每年数学学业考试卷的压轴好戏，因此综合性问题的有效教学尤为重要.众所周知，数学思想方法是解答综合题的灵魂.其中数形结合思想是解答综合题的捷径，方程思想是解答综合题的重要策略，而分类讨论是解答综合题的根本保证.如何落实数学思想方法的教学呢？在复习教学前，我们可以先让学生做，通过对学生不同解法的分析中来洞悉学生的解题思路，从多种解题思路的横向对比中了解学生对问题把握的不同角度与深度，从同一种解题思路的纵向对比中了解学生思维的灵活性与严谨性，这样必将有助于我们找到学生解题中共性的思维局限性与元认知的薄弱点，进而从题海中遴选一些具有代表性、典型性的试题，进行一题精解，帮助学生集零为整，化难为易，达到“会当悟解法，一览众题易”的境界.

1.罗先礼，李孔林.以形助数，简解代数题［J］.中学数学（下），2008（7）.

2.陈新娟.分类讨论思想在解题中的应用［J］.考试周刊，2008（17）.

3.莫裕全.方程思想在数学解题中的应用［J］.中学教学参考，2009（20）.

4.夏丽琼.有关初中数学动态几何问题的思考［J］.现代阅读（教育版），2012（18）.