水下细长体结构“流-刚-弹耦合”特性及方法
张 成,刘志忠
(中国舰船研究设计中心,湖北 武汉 400064)
水下细长体结构“流-刚-弹耦合”特性及方法
张 成,刘志忠
(中国舰船研究设计中心,湖北 武汉 400064)
为对水下细长体的流固耦合特性进行分析,本文建立细长体结构的平面运动学方程。为捕捉结构的振动特性,采用双渐进法给出与之相应的流体动力学方程,形成以“流-刚-弹耦合”为特点的方程组。在时域中推进编程求解耦合方程组,得到结构的刚体运动轨迹、弹性振动情况。并与传统有限元方法进行对比,验证本文方法的正确性及合理性。以此为理论依据,对潜艇结构的“流-刚-弹耦合”特性进行分析。研究表明:水下细长结构在水动压力的作用下,流体、刚体运动、弹性振动存在着耦合现象。本文将刚体运动与弹性振动分别求出,直观体现了“流-刚-弹耦合”这一现象。
流-刚-弹耦合;双渐进法;水弹性振动;流固耦合
0 引 言
水下结构物在水动压力载荷或爆炸冲击载荷作用下,产生刚体运动的同时伴随着弹性变形,其中弹性变形包含整体的变形和局部的振动。对于水下结构物来说,其刚体运动及弹性振动的影响不同。刚体运动直接影响结构的运动姿态,但刚体运动本身所消耗的能量并不会使结构产生应力或变形,也不会使结构破坏,但弹性振动会影响结构本身的应力以及变形,振动过大还会产生塑性变形,甚至产生破口等破坏现象[1-4]。因此需要将水动力载荷及外力载荷共同作用下结构产生的刚体运动与弹性振动分开分析,尽量使外力做功转化为刚体运动的动能,减少弹性振动动能,必然有益于降低结构的破坏及毁伤。
目前,在计算结构上某一点的运动时一般采用有限元法或边界元法[5-10],这样得到的轨迹包括整个结构的刚体运动和该点在结构局部坐标系下的弹性振动之和。需要研究的是,结构上各点的弹性振动随时间的变化情况,这就需要把这2种运动分离开来,并能直观地表示。为此,最容易想到的是,用合位移减掉质心点的运动轨迹即是各点的弹性振动。但是质心点的运动也包含了它本身的弹性振动。因此必须建立一个描述结构刚体运动的坐标系和一个描述结构各质点局部变形的随动坐标系,刚体位移R加上局部位移r即构成质点的绝对位移,以此建立各质点的运动方程[11-13],并分别求解R和r即可将刚体运动和弹性振动分开。
本文以细长对称柱体为研究对象,建立潜体的运动学方程,同时结合双渐进法(又叫DAA法)建立流体的动力学方程[14],研究无限水域“流固耦合”效应。研究成果可用于潜射导弹、潜艇、水下管道、深海立柱等海洋工程结构的设计中。
1 基本理论
1.1 结构运动方程

图1 坐标系示意图Fig.1 The coordinate system

(1)

系统动能表达式如下:

(2)
系统势能表达式如下:


(3)
其中M为结构总质量。
物面上任意点的坐标用(x,γ)表示,其中γ为截面自z轴顺时针方向转角(见图2),a(x)为x截面的半径,φ(x)为结构物面的斜率见图3,作用于面元dA=(a(x)/cosφ(x))dxdγ上的压力p(x,γ),剪应力τm(x,γ)和τγ(x,γ)。令δu′和δw′表示这个面沿x方向和z方向的虚位移(见图3)。

图2 微元面Fig.2 The infinite surface

图3 轴对称体微段dxFig.3 The infinite length ‘dx’ of the symmetric body
将虚位移分解为dA垂直方向和剪切方向并乘以相应的应力便得到外力在这个单元面上所做的虚功:

(4)
式中:结构质心产生水平虚位移δX投影到u和w方向分别为δXsinϑ和-δXcosϑ;质心产生垂向虚位移δZ投影到u和w方向分别为δZcosϑ和δZsinϑ;产生转动虚位移δϑ在u和w方向形成的虚位移为-δϑa(x)cosγ和δϑx。
将总动能K、弹性变形能U和外力所做的虚功δW应用到非有势力做功的哈密尔顿原理[15]。
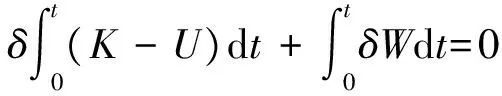
(5)
式中各变分量δX,δZ,δϑ,δu,δw都是独立的。可以得出:
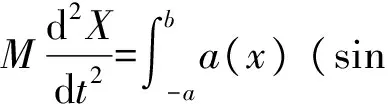

(6)


(7)

(8)

(9)

(10)
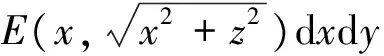
式(6)和式(7)中,结构的刚体运动X,Z与流体压力p有关。压力p是结构与流体交界面处的物面压力,该压力p不仅随流场运动发生变化,而且与结构的物面运动(含结构刚体运动、弹性振动)息息相关。在下文DAA法的推导中可进一步看到物面压力p与结构的刚体运动、弹性振动有关,所以式(6)和式(7)体现了结构的运动与流体压力之间的流固耦合特性。
式(8)中刚体运动参数θ与弹性振动参数u和w、流体压力p有关,而压力p与结构的物面运动(含结构刚体运动参数X,Z,θ,弹性振动参数u和w)息息相关。水动压力把刚体运动X,Z,θ和弹性振动u,w耦合在一起。这些耦合现象的本质仍然是流固耦合,为了对结构的运动(刚体运动和弹性振动)进行更深入解析,本文提出“流-刚-弹耦合”这一说法。
1.2 考虑可压缩性的水动压力计算方法
前面通过推导得出潜体结构的运动微分方程,下面讨论潜体结构表面水动压力的计算方法。在计算流固耦合问题时,采用考虑可压缩性的势函数微分方程式[14]:

DAA法就是从上述控制方程的基础上经推导得到。DAA法的基本方程如下[2]:
1)一阶双渐近法方程DAA1

2)二阶双渐近法方程DAA2

(11)
式中:ps为流体中的散射压力;pi为入射波压力;Mf为流体质量矩阵;Ωf为流体频率矩阵;Af为流体单元的面积矩阵;uI为入射波速度;x为结构位移;G为坐标转换矩阵。

(12)
式中:P=ps+pi,即总的流场动压力值;φ为流场速度势。

(13)
式(13)中的流场散射压力ps通过求解DAA方程式(11)得到,入射波压力pi作为已知条件,流场总速度势φ即可得解。在得到流场速度势的基础上,可以通过伯努利方程得到流场动压力计为Pd。

(14)

(15)
式中:V为结构运动速度。求解式(15)即得到考虑非线性效应的流场动压力P。
2 方程组的求解
在文献[14]中对DAA法求流场动压力P进行了详细介绍,下面对结构运动方程作简要介绍。
因为结构动力学响应中通常低频成分是主要的,从计算精度考虑,允许采用较大的时间步长。因此,本文采用应用最为广泛的无条件稳定的隐式算法Newmark方法[16]。它采用下列假设:

(16)
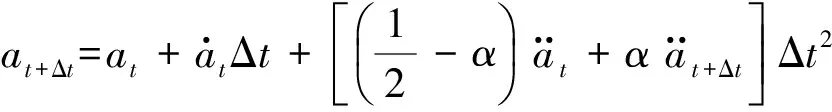
(17)

3 方法对比验证
本文列出了水下细长结构的水弹性振动耦合方程和水动压力方程。为验证本文方法的合理性,通过对细长圆柱壳在水下运动的求解与传统有限元方法求解的结果进行对比。

图4 柱体模型Fig.4 The cylinder model

图5 柱体一阶模态(频率21 Hz)Fig.5 The first mode of the cylinder(the frequency 21 Hz)
圆柱壳半径为r=0.5 m,长度L=6 m,壳厚h=5 m,弹性模量取E=1.1 E11,泊松比ε取0.3,总质量M=11 386 kg,转动惯量J=28 246 kg·m2。坐标系取在其质心点处,沿水平方向有3.5 m/s初速度,沿垂直方向有10 m/s的初速度,如图4所示。图5为圆柱壳网格剖分情况和一阶自由振动模态。

图6 质心轨迹曲线Fig.6 The trace of the barycenter

图7 偏角时历曲线Fig.7 The history curve of the offset angle

图8 垂向速度时历曲线Fig.8 The history curve of the vertical velocity

图9 横速度时历曲线Fig.9 The history curve of the horizontal velocity
通过图6~图9可以看出,2种解法得出的圆柱壳刚体运动轨迹几乎完全一致,证明本文计算方法与传统结构动力学计算方法得出的结果吻合的很好。但是传统有限元解法很难直观得出结构上各点的弹性振动轨迹,在传统解的刚体运动轨迹里包含了弹性振动的成分,由于模型的弹性振动十分微小,故在图6~图9中的传统解中未体现出弹性振动的成分。采用本文计算方法求解得出的弹性振动曲线如图10所示。

图10 不同时刻柱振动曲线Fig.10 The vibration curves at the different time
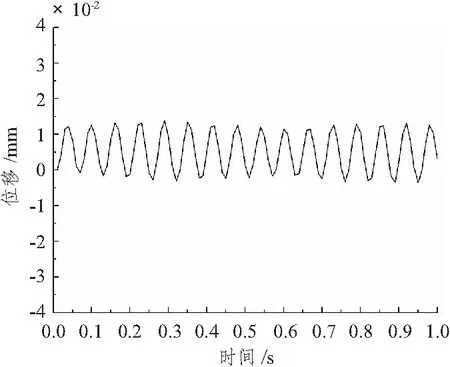
图11 柱体质心弹性振动时历曲线Fig.11 The history curve of the elastic vibration at the center of the cylinder
图10表示柱体不同时刻的振动曲线,其中每条曲线表示某一时刻柱体轴线的弹性变形情况。可以看出,该工况下柱体弹性振动主要以1阶和2阶弹性振动为主。图11所示为圆柱壳质心点处弹性振动的轨迹,该点处的振动轨迹接近于正弦曲线。这主要是由于柱体为对称结构,质心处于对称中心的位置,并且该工况下结构的弹性振动表现为1阶弹性振动,故质心点处的振动时历曲线接近正弦曲线是合理的。该曲线振动周期为0.064左右,即其振动频率为15.6左右,比1阶固有频率小,说明水动压力产生的附加质量降低了柱体的振动频率。

图12 柱体顶部弹性振动时历曲线Fig.12 The history curve of the point on the top of the cylinder

图13 柱体尾部弹性振动时历曲线Fig.13 The history curve of the point on the end part of the cylinder
刚弹耦合方法的优越性体现在采用传统的结构动力学计算方法不能将刚体运动与弹性振动分开,而采用本文的方法可将弹性振动单独提取出来。
4 潜艇模型在均匀来流作用下的运动
以潜艇模型在均匀来流作用下的运动为例,研究非均匀截面结构的刚体运动和弹性振动。为了减小计算量选取潜艇缩比模型进行计算,潜艇缩比模型长L=6 m,最大直径D=0.7 m,厚h=5 mm,弹性模量E=2.1 E11,总质量M=1 574.6 kg,转动惯量I=4 000 kg·m2,垂直潜艇方向均匀来流速度10 m/s,潜艇初始时刻静止。计算模型如图14所示。

图14 潜艇模型Fig.14 The submarine model
图15给出了均匀流作用下的潜艇运动。流体力作用点在潜艇结构质心之上,产生一顺时针的力矩。使潜艇在水中发生偏转,直到潜艇的轴线方向与来流方向一致。
采用刚体弹性体耦合的方法计算潜艇运动可提取潜艇结构的弹性振动如图16~19所示。图16表示柱体不同时刻的振动曲线,其中每条曲线表示某一时刻柱体轴线的弹性变形情况。从图16可以看出,在本文设置的工况作用下结构的弹性振动以四阶以上弹性振动为主,也有部分时刻以2、3阶弹性振动为主。图17~图19分别表示潜艇的头部、中部、尾部各点振动随时间的变化情况。其中头部和质心点处振动的幅度相近,而尾部的振动幅度较大,这与潜艇的结构特征情况是相吻合的。由图17中频域曲线可以看出在该工况下,结构上各质点的振动频率成分分别为3.2 Hz,18.1 Hz,43.0 Hz,表明在水动压力作用下结构的振动以低频振动为主。
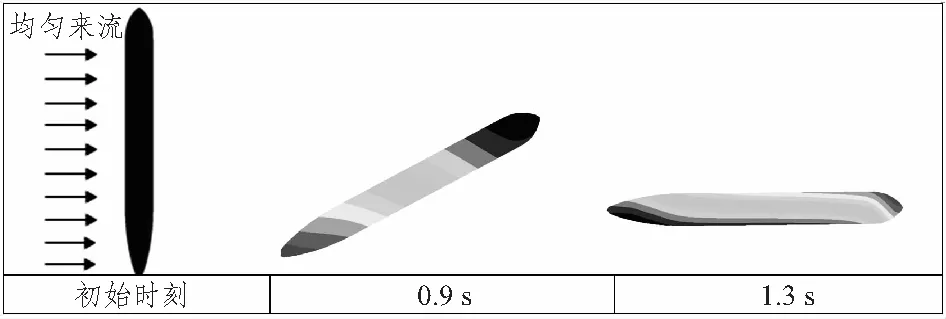
图15 潜艇刚体运动Fig.15 The rigid movement of the submarine

图16 不同时刻潜艇振动曲线Fig.16 The vibration of the submarine at different times

图17 潜艇头部弹性振动频域与时域曲线Fig.17 The vibration curve of the top submarine in the frequency domain and the time domain

图18 潜艇质心弹性振动时历曲线Fig.18 The vibration curve of the barycenter of the submarine

图19 潜艇尾部弹性振动时历曲线Fig.19 The vibration curve of the afterbody of the submarine
5 结 语
本文在计算流体力时,采用考虑可压缩性的双渐近法,用于捕捉结构的弹性振动特性,同时将结构的刚体运动和弹性振动分离开来,将流固耦合系统中结构的弹性振动特性很直观的展现出来。得到结论如下:
1)在水动压力的作用下,不仅结构与流体之间存在耦合,而且结构的刚体运动与弹性振动之间也存在耦合现象。
2)壳体结构在水下运动时,其振动特性表现为以低频振动为主。
3)结构在水中运动时的总体弹性振动的动能远小于刚体运动的动能,因此水结构在水中稳定运行时,不会产生塑性变形或破坏。
本文为了简化问题,选取细长对称壳体为研究对象,对于舰船等结构不太适合。在以后的研究工作中还将考虑结构的非对称性,以及考虑非细长结构的“流刚弹耦合”问题,并将对爆炸冲击载荷作用下的“流刚弹耦合”现象进行分析。
[1] 宁建国,王成,马天宝.爆炸与冲击动力学[M].北京:国防工业出版社,2010.
[2] 黄晓明,朱锡,牟金磊,等.圆柱壳在水下爆炸作用下鞭状响应试验研究[J].哈尔滨工程大学学报,2010,31(10):1278-1285.
HUANG Xiao-ming,ZHU Xi,MU jin-lei,et al.Study on the whipping response of a stiffened cylindrical shell in an underwater explosion[J].Journal of Harbin Engineering University,2010,31(10):1278-1285.
[3] 董海,刘建湖,吴有生,等.水下爆炸气泡脉动作用下细长加筋圆柱壳的鞭状响应分析[J].船舶力学,2007,11( 2):250-258.
DONG Hai,LIU Jian-hu,WU You-sheng,et al.Whipping response analysis of slender stiffened cylindrical shell subjected to underwater explosion with bubble pulse[J].Journal of Ship Mechanics,2007,11(2):250-258.
[4] 李玉节,张效慈,吴有生,等.水下爆炸气泡激起的船体鞭状运动[J].中国造船,2001,42(3):1-7.
LI Yu-jie,ZHANG Xiao-ci,WU You-sheng,et al.Whipping response of ship hull induced by underwater explosion bybble[J].Shipbuilding of CHINA,2001,42(3):1-7.
[5] GU M X,WU Y S,XIA J Z.Time domain analysis of non-linear hydroelastic response of ships[J].In:Proc.Of 4th PRADS,Varna,Bulgaria,989.
[6] 王朝晖,夏锦祝,吴有生.波浪引起的弹性船体响应的时域数值模拟[J].中国造船,1995,131(4):91-96.
WANG Zhao-hui,XIA Jin-zhu,WU You-sheng.Time domain numerical simulation of wave-induced responses of elastic ships[J].Shipbuilding of CHINA,1995,131(4):91-96.
[7] 顾学康,段文洋.船体在波浪中的非线性水动压力[J].船舶力学,2001,5(6):27-39.
GU Xue-kang,DUAN Wen-yang.Nonlinear hydrodynamic pressures on ship hulls in waves[J].Journal of Ship Mechanics, 2001,5(6):27-39.
[8] SIMA C,ZHANG X C,WU Y S. Applications of boundary element method in viscous fluid-structure coupling motion problems[J].J. Ship Mech.,2002(3):35-39.
[9] 陈徐均,吴有生,崔维成.海洋浮体二阶非线性水弹性力学分析——二阶力对浮体振动时间响应的影响. 船舶力学[J].2003,7(2):11-20.
CHEN Xu-jun,WU You-sheng,CUI Wei-cheng.Second order nonlinear hydroelastic analyses of floating bodies—effect of second-order forces to time response of vibration[J].Journal of Ship Mechanics,2003,7(2):11-20.
[10] DU S X.A general theory for the hydroelastic response of a structure manoeuvring in viscous fluid[J].J.Ship Mech.,1999(3):21-34.
[11] 陈伟民,李敏,郑仲钦,等.细长轴对称体的水弹性振动特性分析[J].中国科学, 2010, 40(9):1165-1173.
CHEN Wei-min,LI Min,ZHENG Zhong-qin,et al. Hydroelastic dynamic characteristics of a slender axis-symmetric body[J].Physics, Mechanics & Astronomy,2010,40(9):1165-1173.
[12] 夏锦祝.细长浮体的水弹性力学理论[D].无锡:中国船舶科学研究中心,1994.
[13] 陈徐均,董克,潘小强,等.海洋浮体水弹性力学研究历史与现状[J].解放军理工大学学报(自然科学版),2003,4(6):41-49.
CHEN Xu-jun,DONG Ke,PAN Xiao-qiang,et al.Existing hydroelasticity theories of ocean floating bodies[J].Journal of PLA University of Science and Technology,2003,4(6):41-49.
[14] 姚熊亮,孙士丽,陈玉,等.非线性双渐进法应用于水中结构瞬态运动的研究[J].振动与冲击, 2010,29(10):9-15.
YAO Xiong-liang,SUN Shi-li,CHEN Yu,et al.Transientm otions of sub merged structures with nonlinear fluid-structure interaction method[J].Journal of ibration and shock,2010,29(10):9-15.
[15] 鹫津久一郎. 弹性和塑性力学中的变分法[M].北京:科学出版社,1984.
[16] 王勖成,邵敏.有限单元法基本原理和数值方法(2版)[M].清华大学出版社,1997,448-454.
Research on the fluid-rigid-elastic coupling characteristics of the underwater slender structures and its method
ZHANG Cheng,LIU Zhi-zhong
(China Ship Development and Design Center,Wuhan 430064,China)
To analyze the fluid structure coupling property for the underwater slender structures, in the paper it gives the plane kinematic equations;to get the vibration characteristics, the DAA method is adopted giving the corresponding hydrodynamic equations. And then the equations set characterized by ‘rigid-elastic coupling’and ‘fluid-structure coupling’ are formed. According to the specialties of the movements of the slender structures in water, the rational simplified methods and decoupled methods are given. The coupled equations are solved in the time domain to get the rigid movement of the structure, the elastic vibration and the pressure distribution. The results are compared with that of the traditional methods to validate the correctness and rationality of the method in the paper. Based on the method in the paper, the rigid-elastic coupling characteristics and fluid structure coupling characteristics are analyzed. The conclusion indicates that the rigid movements and the elastic vibration of the underwater slender structures are coupled and these two kinds of movement are solved separately to reflect the coupling phenomenon.
fluid-rigid-elastic coupling;DAA;hydroelastic vibration;fluid structure interaction
2013-09-13;
2013-11-13
张成(1987-),男,硕士,工程师,研究方向为结构动力学。
U664.113
A
1672-7649(2014)09-0025-07
10.3404/j.issn.1672-7649.2014.09.005

