从一道试题谈开放题的有效解答

杨传冈

【例题展示】

如果从这四种水果中选择三种，搭配成一个售价是60元的果篮（不考虑篮子的价钱），可以怎样选择？分别写出水果的名称和数量（整千克）。

【数据链接】

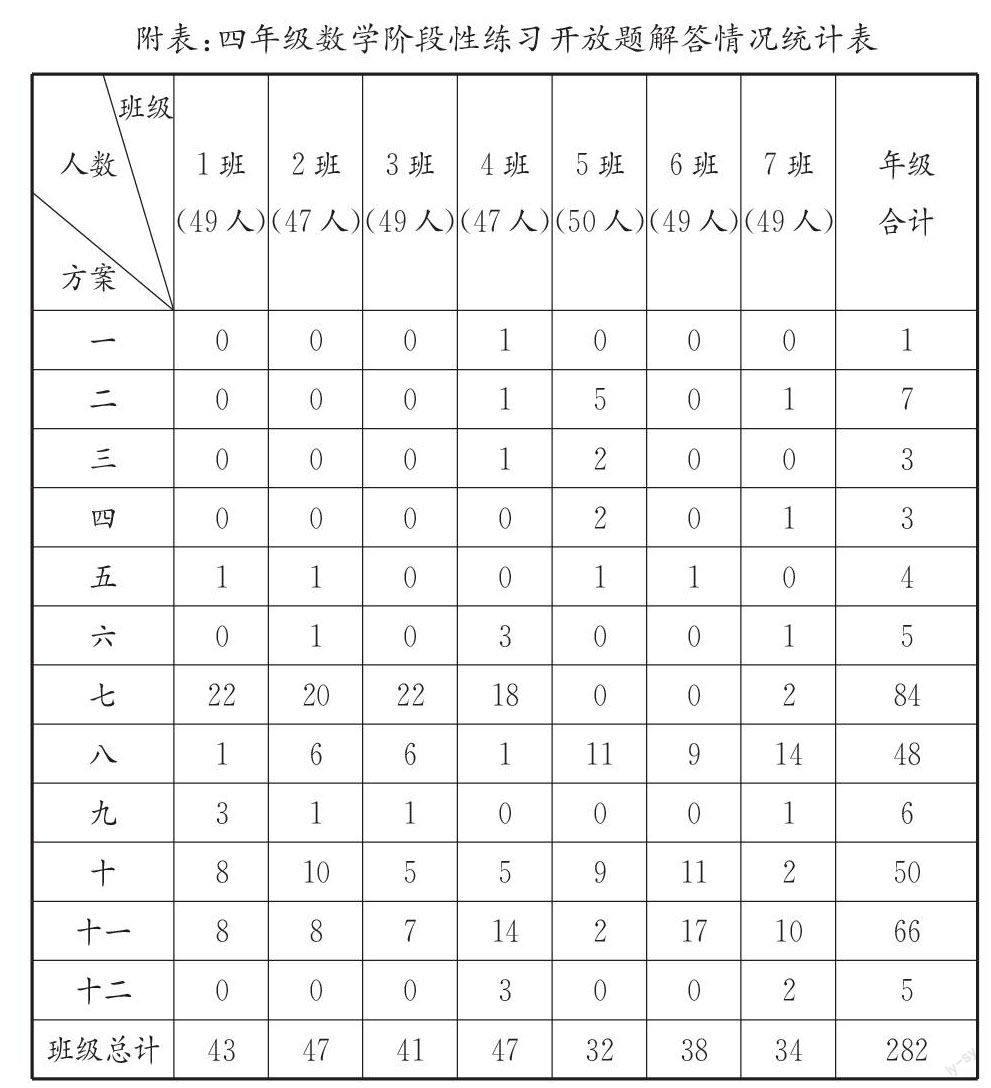
这是四年级数学练习中的一道开放性习题，符合题意的答案不唯一。试题要求并不高，只要写出一种可能即可，从答卷情况来看，学生的答案精彩纷呈。仔细对全年级所有学生的考卷进行梳理、统计后的结果令人振奋：全部12种答案学生均有涉及，充分展示了开放题教学实验后，学生的思维品质明显提升，思维的广阔性得到有效的锻炼。

【数据分析】

瑕不掩瑜，学生在不同算法的选择上表现出较大差异。从思维的精确性看，四年级各班级之间的差距比较明显，2班和4班均达到了100%，1班和3班整体情况较好，而5班仅64%，7班也仅为69？郾4%，6班为77？郾6%，由此可知不同班级开放题教学的实效性存在较大差距；从思维的广阔性看，不同班级也表现了较大差距，其中7班出现了10种不同算法，4班出现了9种不同算法，6班仅出现了4种不同算法，3班出现了5种不同算法；1班出现了6种不同算法；从思维的独特性看，差异表现更强烈，全年级选择第一种方案的仅有1人，令人遗憾的是第一、二、三、四、十二等五种方案，1班、2班、3班、6班完成的学生人数均为0人，选择第七、十、十一种方案的人数则分别达到了84人、50人、66人，由此亦能反映出学生创造性思维的培养任重道远。（数据见附表）

【教学思考】

综合上面的统计信息，结合个人日常对开放题教学的实践及思考，笔者以为要帮助学生有效解答开放题，需要关注下面几个维度。

一、问题情境要善于诱发直觉思维

数学开放题没有固定的解题模式，需要学生深刻、主动地思考，从纷繁的信息中筛选有用条件，调动自己已形成的全部知识储备来设计方案，通过不断尝试、探索、否定、重组、再试，直至捕获直觉念头。小学生囿于年龄的限制，其思维更倾向于形象思维，故开放题的情境设置须有助于诱发学生的直觉思维，帮助学生激活特定的认知结构，从而有效实现问题的解决。

题中橙子的有关信息是“4千克28元”，其余水果都是单价。题目要求由三种水果组成水果篮，这种条件呈现方式从某种意义上来说，给了学生一种强烈的心理暗示。他们会主动寻求后三种水果价格之间的内在联系，不难发现菠萝和荔枝的单价和为20元，而哈密瓜的单价为5元，由此可轻易得到两种不同的方案，即菠萝和荔枝的数量均为1千克，哈密瓜的数量为8千克；菠萝和荔枝的数量分别为2千克，哈密瓜的数量为4千克，这两种方案完全是一种类型的两个分支，相互联系在一起，得其一就能知其二。学生的解答也恰如我们所预测的，给出上述解答的共有116人次，占全年级正确答案的41？郾34%。这也正如波利亚所说：“在你找到第一个蘑菇时，继续观察，也许就能发现一堆蘑菇。”

二、相关数据要有利于学生进行数据建模

数学开放题学习的重要目标之一就是要发展小学生的思维，提升思维品质，编制时要充分体现这一核心要义，重点关注问题内容所包含的对思维深度、广度、严密性、灵活性与批判性的考量。四年级的学生形象思维有余而抽象思维较弱，在数据处理上常常受现有知识经验的影响，更多地从四则运算着手。为了贴近学生实际、凸显训练重点，开放题要最大限度地降低题意的理解难度及相关数据的繁琐程度，把着眼点聚焦于对学生思维变化的观察，思维习惯的训练及思维品质的提升上。

以本题为例，各种水果单价的数据都比较小，这就为学生数据建模提供宽松的外部环境。当学生明晰了橙子的单价为7元后，接下来要做的是从7、5、8、12这4个数中选择3个，累加后和是60，从而引发4种建模趋向，即7、5、8；7、5、12；7、8、12；5、8、12（前文已讨论过）。从学生答题的统计数据来看，“7、5、12”这组条件受到了同学们的青睐，方案二、四、七、八均是由此延伸而来，相应答题的学生人数为7、3、84、35人，合计占了全年级答对总数的45？郾75%。但值得注意的是学生对于“7、5、8”这组条件似乎有一些思维方面的障碍，延展出的解答方案一、三、五、六的人数仅分别为1、3、4、5人，总计仅占全年级答对总数的4？郾61%。特别是前三种水果的单价和为20元，每种各买3千克这种方案全年级仅有5人，学生对这一显而易见的数学现实的漠视，其背后潜藏着的思维深层次原因到底是什么，值得我们进一步探讨。

三、问题解决评价不能唯方案数量论

数学开放题解题思路的多样化特征能最大限度地吸引学生的注意力，解题答案的不唯一能促进不同层次学生的个性化学习，特别是部分学困生也能从开放题的解决过程中获得成功的喜悦，积累数学解题经验，渐渐找回学好数学的信心。因此，在开放题教学的初级阶段，教师要降低门槛，针对不同学生提出不同的问题解决要求，考查时明确只要得出一种正确结果就得满分，最大限度地保护学生学习开放题的热情和兴趣。经过一段时间的系统学习与训练，再逐渐加大对问题答案呈现数量的要求。

本题中，考虑四年级学生才开始系统学习数学开放题，并且试题没有明确问题的答案数量，只要写出一种正确答案就能得满分。经过梳理，学生共给出了281人次的正确答案，占总人数的80？郾29%，仅有5名学生主动给出了两种以上的答案，这也说明小学生在没有明确要求时主动呈现多种答案的意识尚未清晰。

开放题讲评时，教师要有针对性地引导不同层次的学生了解自己在解决开放题时的进步，鼓励学生反思自己的解题历程，聆听他人与众不同的见解，碰撞彼此的观点，擦出智慧的火花，借此培养学生的自我评价能力，同时鼓励更多学生能根据实际情况主动给出开放题的不同答案。

（作者单位：江苏省盐城市第二小学）