轴承滚子非常态运动弹流润滑分析*

武宁宁，李书义，赵小军

(青岛理工大学(临沂) 机电工程系，山东 青岛 273400 )

轴承滚子非常态运动弹流润滑分析*

武宁宁，李书义，赵小军

(青岛理工大学(临沂) 机电工程系，山东 青岛 273400 )

针对工程中轴承工作时滚子发生非常态运动问题，建立滚子非常态运行模型，利用数值分析方法，研究了滚子非常态运行时滚子与外圈、滚子与内圈间的弹流润滑特性。结果表明，轴承滚子微小偏斜时，会造成滚子与外内圈之间一端油膜膜厚减小，接触压力增大，另一端变化正相反，其中接触压力的改变较明显，引起偏载现象，且滚子与内圈间的情况更严重；轴承滚子小角度歪斜时，对滚子与内外圈间膜厚和应力分布情况影响都不大。

轴承;滚子偏斜;滚子歪斜;有限长线接触;弹性流体动力润滑

Abstract: For roller non-normal motion problems of engineering bearing, roller non-normal operation model is established. Using the method of numerical analysis, Elastohydrodynamic lubrication characteristics of roller outer ring and roller and inner ring under roller non-normal operation is studied. Results show that, film thickness decreases and pressure increases in one side of roller when small deflection of bearing roller, however, the other side of roller is the opposite. Moreover the change of the contact pressure is more noticeable which causing unbalance loading phenomenon. It is more serious between roller and inner ring. When roller is small deflected angle, the distribution of film thickness and stress in roller and inner is small impacted.

Key words: bearing; roller deflection; roller skew; finite line contact; EHL

0 引 言

近年来对于正常态下圆柱滚子轴承的弹流润滑问题已有较多研究分析，但实际工程上轴承工作时常常出现其滚子的非常态运行，这是由于轴承受到与其相连部件振动的影响；或是轴承滚子与保持架间碰撞摩擦；或轴承安装时内外圈轴线不同轴等原因造成，这会降低轴承运行精度和寿命，那么就有必要针对于此现象进行研究分析。康献民等[1]研究了滚针轴承歪斜下受力特点，Johns和Gohar[2]分析了轴承滚子偏斜下其修形对接触力的影响，以及多位学者[3-6]基于滚子副干接触条件下滚子偏斜的研究。实际上轴承必须在润滑条件下运行，文献[6]、[7]虽然置于弹流润滑条件下，但都是以滚子与无限大平面为接触模型，与实际工作轴承情况有所差异，笔者将以轴承N305ECP为原型，针对于滚子的非常态运行问题展开讨论。

1 轴承模型

笔者根据实际轴承建立相应模型如图1(a)，讨论轴承在Ⅰ、Ⅱ两接触区域滚子非常态运行下的弹流油膜和压力分布。如图1(b) 所示，滚子的非正常运行本质上可归为两大类：一类是滚子绕x轴发生一定转动，转过的角度称为偏斜角，α；另一类是滚子绕z轴发生一定转动，转过的角度称为歪斜角，β。

图1 滚子轴承模型及其局部剖视图

2 基本方程

Reynolds方程为：

(1)

式中：x、y为坐标变量，m；p为润滑油压力，Pa；h为油膜厚度，m；η为润滑油的粘度，Pa·s；ρ为润滑油的密度，kg/m3；ue、ve为x、y轴卷吸速度，m/s。

方程式(1) 的边界条件为:

式中：下标“in”和“out”表示计算域的边界。

膜厚方程：

滚子与外圈接触Ⅰ：

(y≤0时，取 +；y>0，取)

(2)

滚子与内圈接触Ⅱ：

(y≤0时，取 +；y>0，取)

(3)

粘压关系：

η=η0exp {A1[(1+A2p)z0-1]}

(4)

式中：η0为环境粘度，Pa·s；A1=lnη0+9.67，A2=5.1×10-9Pa，z0=ψ/(A1A2)，ψ为Barus粘压系数，Pa。

密压关系为：

ρ=ρ0[1+A3p/(1+A4p)]

(5)

式中：ρ0为润滑油的环境密度,kg/m3;A3=0.6×10-9Pa，A4=1.7×10-9Pa。

载荷方程为：

(6)

式中：w为外载荷，N。

数值方法是在方程式(1)～(6)无量纲化的基础上采用多重网格法和多重网格积分法[8]计算。使用5层网格，最稠密网格上节点数为256×1024。收敛判据为压力、载荷的相对误差均小于0.1%。

3 结果与讨论

设润滑油为牛顿流体，基本参数：η0= 0.08 Pa·s，ψ= 2.2×10Pa，E′=2.26×1011Pa，w=0.899 47×10N，pH=0.5 GPa，ue= 2.08 m/s，ve= 0。滚子总长度L=10 mm，滚子有效长度l=9 mm，滚子半径Rx= 10 mm，端部相切圆弧半径Ry= 5 mm，滚子接触外圈半径Rx1=54 mm，滚子接触内圈半径Rx2=44 mm。

3.1 滚子偏斜

图2、3分别给出了轴承模型中Ⅰ、Ⅱ接触区滚子常态与非常态 (偏斜) 下膜厚和压力的三维图。可见，在常态下轴承运行时，滚子与外内圈间接触区的膜厚和压力关于Y= 0对称分布，除端部外整个接触区分布均匀，由于端泄问题引起端部压力升高而膜厚减小。

图2 外圈与滚子接触区Ⅰ在滚子偏斜前后膜厚和压力的三维图

图3 内圈与滚子接触区Ⅱ在滚子偏斜前后膜厚和压力的三维图

在非常态(偏斜)时轴承运行时，滚子与外内圈间接触区的膜厚和压力关于Y= 0不再对称分布，油膜厚度改变量相对较小，压力变化较为明显，即接触区一端压力变大，而另一端减小，引起接触力集中。所以，滚子偏斜对接触区Ⅰ、Ⅱ都产生了不利影响。

图4给出了轴承工作时不同的非常态情况 (不同的滚子偏斜角度) 在X= 0截面膜厚和压力的分布曲线图，可明显看出，随着滚子偏斜角度值的增大，一端压力逐渐增大、膜厚逐渐减小，另一端变化正好相反，若偏斜角度达到一定值时，甚至出现一端端部接触压力接近为0，而另一端却集中了大部分载荷，且膜厚厚度较薄，润滑效果较差，严重时可能会出现油膜破裂，导致润滑失效。

为了研究滚子非常态运动对接触区Ⅰ、Ⅱ影响程度的不同，表1给出了关于Y= 0对称的两截面 (Y= ±3/4L) 上中心膜厚和中心压力的变化规律。显而易见，随着滚子偏斜角度的增大，接触区Ⅰ中的A截面膜厚厚度增加、压力减小，B截面与之相反，而接触区Ⅱ中的A截面膜厚厚度减小、压力增大，B截面与之相反，符合之前得到的变化规律，但A、B截面的的中心膜厚之差Δh和中心压力之差Δp改变的程度不同。对于中心膜厚之差Δh，两接触区其改变量虽不同但数值上相差不大，且油膜膜厚本就改变量不大，

对润滑效果影响小；对于中心压力之差Δp，两接触区其改变量大，并且接触区Ⅱ内其改变程度要比接触区Ⅰ更加剧烈，即同样滚子偏斜角下滚子与内圈接触区偏载现象更加明显。

图4 在X= 0截面上偏斜角度变化对膜厚和压力的影响

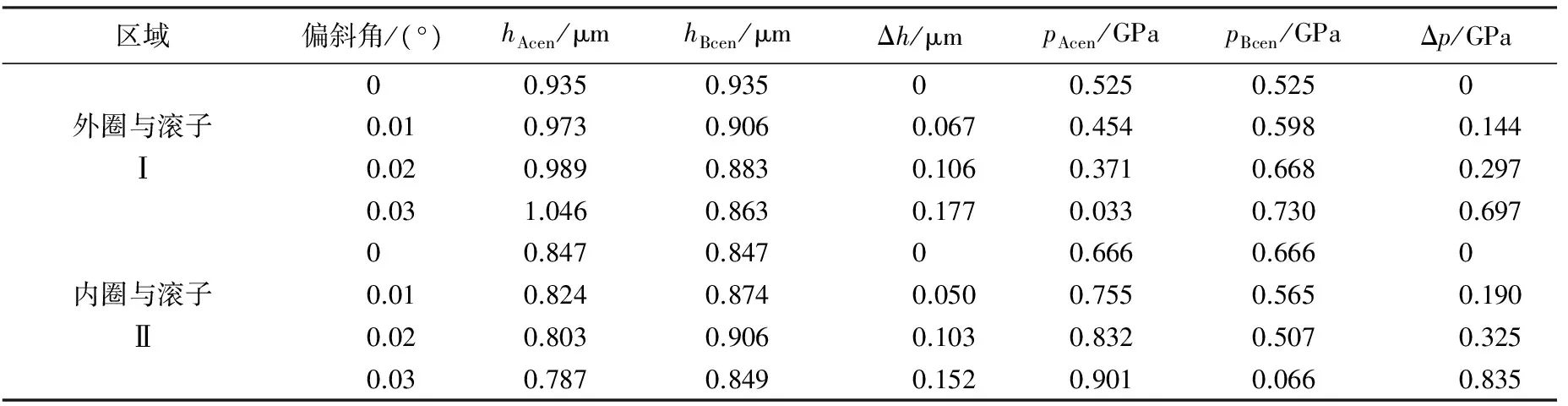
区域偏斜角/(°)hAcen/μmhBcen/μmΔh/μmpAcen/GPapBcen/GPaΔp/GPa外圈与滚子Ⅰ内圈与滚子Ⅱ00．9350．93500．5250．52500．010．9730．9060．0670．4540．5980．1440．020．9890．8830．1060．3710．6680．2970．031．0460．8630．1770．0330．7300．69700．8470．84700．6660．66600．010．8240．8740．0500．7550．5650．1900．020．8030．9060．1030．8320．5070．3250．030．7870．8490．1520．9010．0660．835

3.2 滚子歪斜

图5给出了滚子与外内圈接触区Ⅰ、Ⅱ在滚子歪斜与否两工况下的油膜厚度和压力的等值线图。

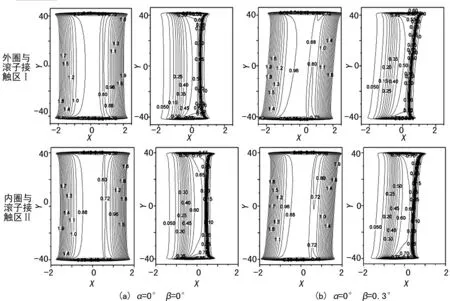
图5轴承中接触区Ⅰ、Ⅱ在滚子歪斜前后膜厚和压力的等值线图

由图5可见，无论滚子歪斜与否，接触区膜厚和压力仍呈现有限长线接触弹流润滑的典型特征，整个接触区呈长条状分布，在不计端部效应的情况下，滚子未发生歪斜时，油膜厚度和压力大体上呈现均匀分布，滚子发生歪斜 (β= 0.3°) 后，滚子与外内圈间的接触区也随之发生歪斜，但油膜厚度和压力沿滚子轴向分布没有出现明显改变。与图2、3对比，虽滚子歪斜角度是偏斜角度的20倍，但对接触区的弹流润滑影响程度明显降低很多。因此，滚子发生非常态运行中，滚子歪斜的不利影响远远低于滚子偏斜的影响。

4 结 论

(1) 轴承滚子发生非常态运行时会改变接触区润滑效果，相对来说，滚子偏斜会严重恶化接触区润滑状态，而滚子歪斜仅造成微弱的不利影响；

(2) 滚子一定微小角度偏斜时，会引起接触区一端压力增大膜厚减小，一端压力减小膜厚增加，即偏载现象，而且滚子与内圈接触区偏载现象更明显，润滑状态恶化更严重；

(3) 滚子一定小角度歪斜时，接触区也会随之发生歪斜，但整个接触区压力和膜厚几乎不发生改变，仅有油膜颈缩处膜厚和第二压力峰略有改变，对润滑效果的影响不明显。

[1] 康献民, 杜春英, 万一夔. 连杆大端滚针轴承滚子歪斜分析[J]. 轴承,2013(1):7-10.

[2] Johns P M，Gohar R．Roller Bearings Under Radial and Eccentricloads[J]．Tribo Int, 1981(13):131-136.

[3] Heydari M，Gohar R．The Influence of Axial Profile on Pressure Distribution in Radially Loaded Rollers[J]．Proc IMechE，Part C，J Mechanical Engineering Science, 1979,21(6)381-388.

[4] Hartnett M．The Analysis of Contact Stresses in Rolling Elementbear-ings[J]．ASME J Ournal of Tribology,1979(101):105-109.

[5] 魏延刚, 葛宰林, 江亲瑜. 高速客车轴箱轴承的偏载分析及轴承滚子非对称修形[J]. 润滑与密封, 2002, 27(2):9-11.

[6] 王爱林, 王庆九, 汪久根. 滚子偏斜对圆锥滚子与内圈接触的影响[J]. 机械设计与研究,2012, 28(1):56-67.

[7] 孙浩洋, 华同曙, 陈晓阳. 对数滚子偏斜时的弹流润滑研究[J]. 中国机械工程, 2013, 24(5):650-653.

[8] 杨沛然．流体润滑数值分析[M]．北京：国防工业出版社，1998．

Elastohydrodynamic Lubrication Analysis of Roller Bearing Non-Normal Operation

WU Ning-ning, LI Shu-yi, ZHAO Xiao-jun

(DepartmentofElectricalandMechanicalEngineering,QingdaoTechnologicalUniversity(linyi)，QingdaoShandong273400,China)

2014-07-04

武宁宁(1983-)，男，山东临沂人，讲师，研究方向：数控技术。

TH117.2

A

1007-4414(2014)04-0047-04